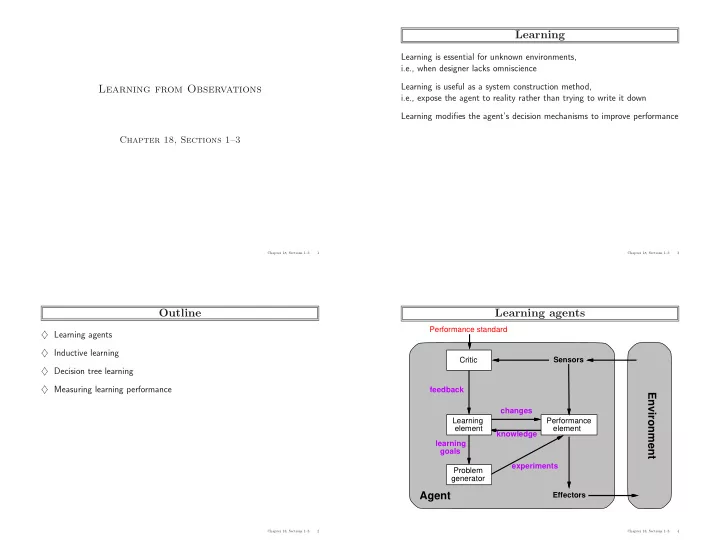
Learning Learning is essential for unknown environments, i.e., when - PowerPoint PPT Presentation

Learning Learning is essential for unknown environments, i.e., when designer lacks omniscience Learning is useful as a system construction method, Learning from Observations i.e., expose the agent to reality rather than trying to write it down Learning modifies the agent’s decision mechanisms to improve performance Chapter 18, Sections 1–3 Chapter 18, Sections 1–3 1 Chapter 18, Sections 1–3 3 Outline Learning agents Performance standard ♦ Learning agents ♦ Inductive learning Critic Sensors ♦ Decision tree learning ♦ Measuring learning performance feedback Environment changes Learning Performance element element knowledge learning goals experiments Problem generator Agent Effectors Chapter 18, Sections 1–3 2 Chapter 18, Sections 1–3 4

Learning element Inductive learning method Design of learning element is dictated by Construct/adjust h to agree with f on training set ♦ what type of performance element is used ( h is consistent if it agrees with f on all examples) ♦ which functional component is to be learned E.g., curve fitting: ♦ how that functional compoent is represented ♦ what kind of feedback is available f(x) Example scenarios: Performance element Component Representation Feedback Alpha−beta search Eval. fn. Weighted linear function Win/loss Logical agent Transition model Successor−state axioms Outcome Utility−based agent Transition model Dynamic Bayes net Outcome Simple reflex agent Percept−action fn Neural net Correct action x Supervised learning: correct answers for each instance Reinforcement learning: occasional rewards Chapter 18, Sections 1–3 5 Chapter 18, Sections 1–3 7 Inductive learning method Inductive learning (a.k.a. Science) Construct/adjust h to agree with f on training set Simplest form: learn a function from examples ( tabula rasa ) ( h is consistent if it agrees with f on all examples) f is the target function E.g., curve fitting: O O X f(x) An example is a pair x , f ( x ) , e.g., , +1 X X Problem: find a(n) hypothesis h such that h ≈ f given a training set of examples ( This is a highly simplified model of real learning: – Ignores prior knowledge x – Assumes a deterministic, observable “environment” – Assumes examples are given – Assumes that the agent wants to learn f —why? ) Chapter 18, Sections 1–3 6 Chapter 18, Sections 1–3 8

Inductive learning method Inductive learning method Construct/adjust h to agree with f on training set Construct/adjust h to agree with f on training set ( h is consistent if it agrees with f on all examples) ( h is consistent if it agrees with f on all examples) E.g., curve fitting: E.g., curve fitting: f(x) f(x) x x Chapter 18, Sections 1–3 9 Chapter 18, Sections 1–3 11 Inductive learning method Inductive learning method Construct/adjust h to agree with f on training set Construct/adjust h to agree with f on training set ( h is consistent if it agrees with f on all examples) ( h is consistent if it agrees with f on all examples) E.g., curve fitting: E.g., curve fitting: f(x) f(x) x x Ockham’s razor: maximize a combination of consistency and simplicity Chapter 18, Sections 1–3 10 Chapter 18, Sections 1–3 12

Attribute-based representations Expressiveness Examples described by attribute values (Boolean, discrete, continuous, etc.) Decision trees can express any boolean function of the input attributes. E.g., for Boolean attributes, truth table row → path to leaf: E.g., situations where I will/won’t wait for a table: Attributes Target A Example A B A xor B F T WillWait Alt Bar Fri Hun Pat Price Rain Res Type Est F F F X 1 T F F T Some $$$ F T French 0–10 T B B F T T X 2 T F F T Full $ F F Thai 30–60 F F T F T T F T X 3 F T F F Some $ F F Burger 0–10 T T T F T F T T Full $ F F Thai 10–30 T F T T F X 4 T F T F Full $$$ F T French > 60 F X 5 Trivially, there is a consistent decision tree for any training set F T F T Some $$ T T Italian 0–10 T X 6 F T F F None $ T F Burger 0–10 F X 7 w/ one path to leaf for each example (unless f nondeterministic in x ) F F F T Some $$ T T Thai 0–10 T X 8 but it probably won’t generalize to new examples F T T F Full $ T F Burger > 60 F X 9 T T T T Full $$$ F T Italian 10–30 F Prefer to find more compact decision trees X 10 X 11 F F F F None $ F F Thai 0–10 F X 12 T T T T Full $ F F Burger 30–60 T Classification of examples is positive (T) or negative (F) Chapter 18, Sections 1–3 13 Chapter 18, Sections 1–3 15 Decision trees Hypothesis spaces One possible representation for hypotheses How many distinct decision trees with n Boolean attributes?? E.g., here is the “true” tree for deciding whether to wait: Patrons? None Some Full F T WaitEstimate? >60 30−60 10−30 0−10 F Alternate? Hungry? T No Yes No Yes Reservation? Fri/Sat? T Alternate? No Yes No Yes No Yes Bar? T F T T Raining? No Yes No Yes F T F T Chapter 18, Sections 1–3 14 Chapter 18, Sections 1–3 16

Hypothesis spaces Hypothesis spaces How many distinct decision trees with n Boolean attributes?? How many distinct decision trees with n Boolean attributes?? = number of Boolean functions = number of Boolean functions = number of distinct truth tables with 2 n rows = 2 2 n Chapter 18, Sections 1–3 17 Chapter 18, Sections 1–3 19 Hypothesis spaces Hypothesis spaces How many distinct decision trees with n Boolean attributes?? How many distinct decision trees with n Boolean attributes?? = number of Boolean functions = number of Boolean functions = number of distinct truth tables with 2 n rows = number of distinct truth tables with 2 n rows = 2 2 n E.g., with 6 Boolean attributes, there are 18,446,744,073,709,551,616 trees Chapter 18, Sections 1–3 18 Chapter 18, Sections 1–3 20

Hypothesis spaces Hypothesis spaces How many distinct decision trees with n Boolean attributes?? How many distinct decision trees with n Boolean attributes?? = number of Boolean functions = number of Boolean functions = number of distinct truth tables with 2 n rows = 2 2 n = number of distinct truth tables with 2 n rows = 2 2 n E.g., with 6 Boolean attributes, there are 18,446,744,073,709,551,616 trees E.g., with 6 Boolean attributes, there are 18,446,744,073,709,551,616 trees How many purely conjunctive hypotheses (e.g., Hungry ∧ ¬ Rain )?? How many purely conjunctive hypotheses (e.g., Hungry ∧ ¬ Rain )?? Each attribute can be in (positive), in (negative), or out 3 n distinct conjunctive hypotheses ⇒ More expressive hypothesis space – increases chance that target function can be expressed – increases number of hypotheses consistent w/ training set ⇒ may get worse predictions Chapter 18, Sections 1–3 21 Chapter 18, Sections 1–3 23 Hypothesis spaces Decision tree learning How many distinct decision trees with n Boolean attributes?? Aim: find a small tree consistent with the training examples = number of Boolean functions Idea: (recursively) choose “most significant” attribute as root of (sub)tree = number of distinct truth tables with 2 n rows = 2 2 n function DTL ( examples, attributes, default ) returns a decision tree E.g., with 6 Boolean attributes, there are 18,446,744,073,709,551,616 trees if examples is empty then return default else if all examples have the same classification then return the classification How many purely conjunctive hypotheses (e.g., Hungry ∧ ¬ Rain )?? else if attributes is empty then return Mode ( examples ) Each attribute can be in (positive), in (negative), or out else 3 n distinct conjunctive hypotheses best ← Choose-Attribute ( attributes , examples ) ⇒ tree ← a new decision tree with root test best for each value v i of best do examples i ← { elements of examples with best = v i } subtree ← DTL ( examples i , attributes − best , Mode ( examples )) add a branch to tree with label v i and subtree subtree return tree Chapter 18, Sections 1–3 22 Chapter 18, Sections 1–3 24