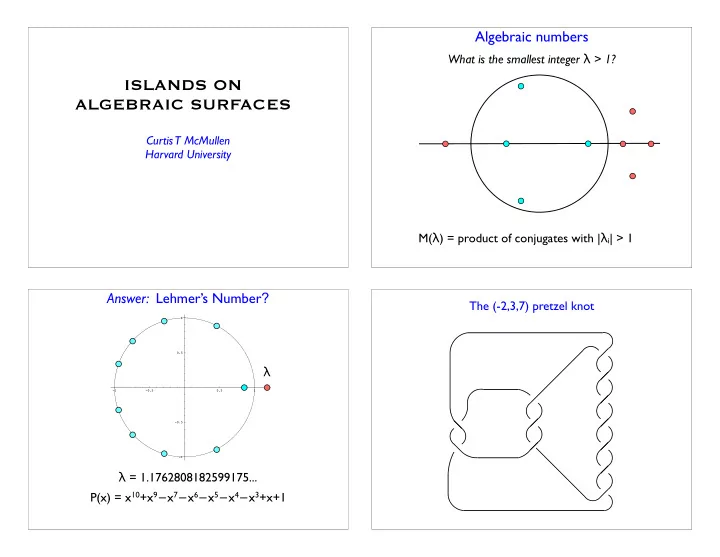

Algebraic numbers What is the smallest integer � > 1? ISLANDS ON ALGEBRAIC SURFACES Curtis T McMullen Harvard University M( � ) = product of conjugates with | � i | > 1 Answer: Lehmer’s Number ? The (-2,3,7) pretzel knot 1 0.5 � -1 -0.5 0.5 1 -0.5 -1 � = 1.1762808182599175... P(x) = x 10 +x 9 � x 7 � x 6 � x 5 � x 4 � x 3 +x+1
Coxeter element Coxeter Groups e 1 e 2 e 3 e 4 e 5 e 6 e 7 e 8 e 9 <e i ,e i > = 2 e 10 <e i ,e k > = 0 or -1 W ⊂ O(n, Z ) : generated by reflections s i in e i Coxeter element w = s 1 s 2 s 3 s 4 ... s 10 Coxeter system λ ( W, S ) det( xI − w ) 1 − x − 3 x 2 − x 3 + x 4 Ah 4 2.36921 Lehmer’s polynomial = det(xI-w) for E 10 (2.26844) (1 + x )(1 − x − 2 x 2 − x 3 + x 4 ) Ah 5 2.08102 1 − 2 x 2 − 3 x 3 − 2 x 4 + x 6 Ah 6 1.98779 (1.96355) (1 + x )(1 + x + x 2 )(1 − 2 x + x 2 − 2 x 3 + x 4 ) Ah 7 1.88320 1 − x 2 − 2 x 3 − 3 x 4 − 2 x 5 − x 6 + x 8 Ah 8 1.83488 (1.82515) (1 + x )(1 − x − x 2 − x 3 + x 4 ) Bh 5 1.72208 1 − x 2 − 2 x 3 − x 4 + x 6 Bh 6 1.58235 The 38 (1 + x )(1 − x − x 3 − x 5 + x 6 ) Bh 7 1.50614 minimal 1 − x 2 − x 3 − x 5 − x 6 + x 8 Theorem. The spectral radius of any w in any 1.45799 Bh 8 Coxeter (1 + x )(1 − x − x 3 + x 4 − x 5 − x 7 + x 8 ) Bh 9 1.42501 Coxeter group satisfies r(w) = 1 or systems (1 + x ) 2 (1 − x − x 2 − x 3 + x 4 ) Dh 6 1.72208 r(w) � � Lehmer > 1. (1 + x )(1 − x 2 − 2 x 3 − x 4 + x 6 ) Dh 7 1.58235 (1 + x ) 2 (1 − x − x 3 − x 5 + x 6 ) Dh 8 1.50614 (1 + x )(1 − x 2 − x 3 − x 5 − x 6 + x 8 ) Dh 9 1.45799 (1 + x ) 2 (1 − x − x 3 + x 4 − x 5 − x 7 + x 8 ) Dh 10 1.42501 (1 + x + x 2 )(1 − x 2 − x 3 − x 4 + x 6 ) Eh 8 1.40127 (1 + x )(1 − x 3 − x 4 − x 5 + x 8 ) Eh 9 1.28064 1 + x − x 3 − x 4 − x 5 − x 6 − x 7 + x 9 + x 10 Eh 10 1.17628
Coxeter system λ ( W, S ) det( xI − w ) Dynamics (1 + x )(1 − x − 2 x 2 − x 3 + x 4 ) 2.08102 K 343 (1 + x ) 2 (1 − 2 x + x 2 − 2 x 3 + x 4 ) K 3433 1.88320 (1 + x ) 2 (1 − 3 x + x 2 ) K 44 2.61803 5 √ K 53 2.15372 (1 + x ) 2 (2 − 3 x − 5 x + 2 x 2 ) 5 √ √ 5 x 3 + 2 x 4 ) K 533 1.91650 (1 + x )(2 − x − 5 x − x 3 − 1 − x 2 − 2 x 3 − x 4 + x 6 L 33433 1.58235 1 − x 2 − x 3 − x 4 + x 6 L 34333 1.40127 5 √ √ 5 x 2 + x 3 − √ 5 x 3 + 2 x 4 L 353 1.84960 2 + x − 5 x − 2 (1 + x )(1 − 2 x + x 2 − 2 x 3 + x 4 ) L 4343 1.88320 1 − x − 2 x 2 − x 3 + x 4 L 443 2.08102 5 √ √ 5 x 3 + 2 x 4 ) 1.36000 (1 + x )(2 − x − 5 x + 2 x 2 − x 3 − L 5333 5 √ √ 5 x 3 + 2 x 4 L 534 1.91650 2 − x − 5 x − x 3 − 5 √ 5 x + 2 x 2 ) L 54 2.15372 (1 + x )(2 − 3 x − 6 1 − x − x 2 − x 3 + x 4 L 633 1.72208 7 (1 + x )(1 + x + x 2 − 4 x cos 2 π / 7) L 73 1.63557 f : X � X holomorphic diffeomorphism √ 3.09066 (1 + x )(1 − 2 x − 2 x + x 2 ) Q 3 (2.89005) of a compact complex manifold √ 2 x 2 − x 3 + x 4 1 − x − x 2 − 2 Q 4 2.57747 √ 2 x 2 − 2 x 3 + x 4 ) (1 + x )(1 − 2 x + x 2 − Q 5 2.43750 (2.3963) What is the simplest interesting dynamical system? (1 + x ) 3 (1 − 3 x + x 2 ) X 5 2.61803 X 6 2.61803 (1 + x ) 4 (1 − 3 x + x 2 ) Bowties Complex Surfaces Theorem (Cantat) A surface X admits an automorphism f : X � X with positive entropy only if X is birational to: • the projective plane P 2 • a complex torus C 2 / � , or • a K3 surface.
Elliptic islands Stochastic Sea A=2 A=2.5 (1+x 2 )(1+y 2 )(1+z 2 )+Axyz = 2 Tame blowup Ergodicity A=8
Complex Orbit A family of K3 surfaces Islands Theorem Synthesis There exists a K3-surface automorphism f : X � X with a complex Number theory: P(t) = det(tI-f*|H 2 (X)) invariant island -- a Siegel disk. Gross-M: P(t) ⇒ f* acting on II 3,19 = H 2 (X,Z) Analysis Torelli: f* ⇒ [X and f:X � X] Hodge theory: study f* on H 2 (X) = H 2,0 ⊕ H 1,1 ⊕ H 0,2 Key ingredient: Degree 22 Salem number of trace -1 Lefschetz: Tr(f*)= -1 ⇔ f has a unique fixed point P P(t) = 1+t-t 3 -2t 4 -3t 5 -3t 6 -2t 7 +2t 9 +4t 10 +5t 11 Atiyah-Bott: f* determines rotation Df P on T P X +4t 12 +2t 13 -2t 15 -3t 16 -3t 17 -2t 18 -t 19 +t 21 +t 22 Transcendence: Df P not resonant Siegel: f ~ linear rotation near P X is not projective!
Rational Surfaces Realization Theorem X = blowup of P 2 at n points The Coxeter element of W n can always be realized by an automorphism F n : X n � X n H 2 (X,Z) ≃ Z 1,n ⊃ K X ⊥ ≃ [E n lattice] of P 2 blown up at n special points. Example: F 3 (x,y) = (y,y/x) (x,y) � (y,y/x) � (y/x,1/x) � (1/x,1/y) � (1/y,x/y) � (x/y,x) � (x,y) Theorem (Nagata) Every automorphism of X lies in the Weyl group W n ⊂ O(Z 1,n ). 3 � X 3 P 2 K X ⊥ = (-3,1,1,...,1) 1 2 10 points on a cuspidal cubic Lehmer’s automorphism F 10 : X 10 � X 10 First case where h(F n ) > 0 Theorem. The map F 10 has minimal positive entropy among all surface automorphisms, namely h(F 10 ) = log( � Lehmer ). (x,y) � (y,y/x) + (a,b)
12 points on 3 lines Synthesis X = blowup of n points on a cuspidal cubic C in P 2 [E n lattice] ≃ Pic 0 (X n ) � Pic 0 (C) ≃ C ! ! Coxeter element w Eigenvalue � of w � ⇒ positions of n points on C 11 points on a conic + line Speed of convergence
Island on a rational surface
Recommend
More recommend