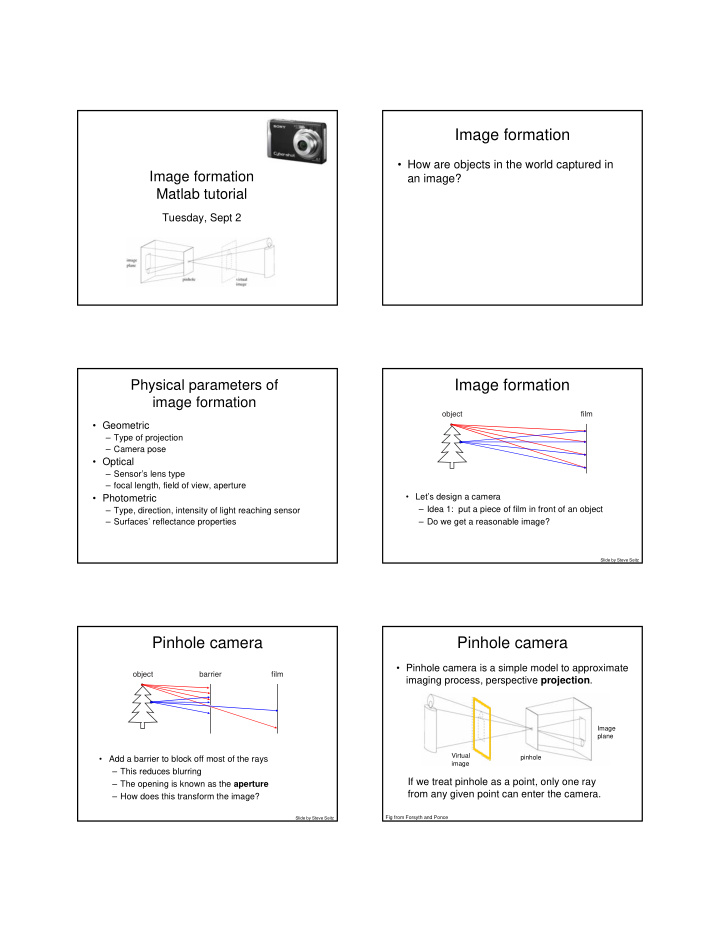
Image formation How are objects in the world captured in Image - PDF document

Image formation • How are objects in the world captured in Image formation an image? Matlab tutorial Tuesday, Sept 2 Image formation Physical parameters of image formation object film • Geometric – Type of projection – Camera pose • Optical – Sensor’s lens type – focal length, field of view, aperture • Photometric • Let’s design a camera – Idea 1: put a piece of film in front of an object – Type, direction, intensity of light reaching sensor – Surfaces’ reflectance properties – Do we get a reasonable image? Slide by Steve Seitz Pinhole camera Pinhole camera • Pinhole camera is a simple model to approximate object barrier film imaging process, perspective projection . Image plane Virtual pinhole • Add a barrier to block off most of the rays image – This reduces blurring If we treat pinhole as a point, only one ray – The opening is known as the aperture from any given point can enter the camera. – How does this transform the image? Fig from Forsyth and Ponce Slide by Steve Seitz

Camera obscura Camera obscura In Latin, means ‘dark room’ Jetty at Margate England, 1898. " Reinerus Gemma-Frisius , observed an eclipse of the sun at Louvain on January An attraction in the late 24, 1544, and later he used this illustration of the event in his book De Radio 19 th century Around 1870s Astronomica et Geometrica, 1545. It is thought to be the first published illustration of a camera obscura..." Hammond, John H., The Camera Obscura, A Chronicle http://brightbytes.com/cosite/collection2.html Adapted from R. Duraiswami http://www.acmi.net.au/AIC/CAMERA_OBSCURA.html Camera obscura at home Perspective effects http://blog.makezine.com/archive/2006/02/how_to_room_ Sketch from http://www.funsci.com/fun3_en/sky/sky.htm sized_camera_obscu.html Perspective effects Perspective effects • Far away objects appear smaller Forsyth and Ponce

Projection properties Perspective effects • Parallel lines in the scene intersect in the image • Many-to-one: any points along same ray map to same point in image • Converge in image on horizon line • Points � points Image plane • Lines � lines (collinearity preserved) (virtual) pinhole • Distances and angles are not preserved • Degenerate cases: – Line through focal point projects to a point. – Plane through focal point projects to line Scene – Plane perpendicular to image plane projects to part of the image. Perspective projection equations Perspective and art • Use of correct perspective projection indicated in • 3d world mapped to 2d projection in image plane 1 st century B.C. frescoes Image • Skill resurfaces in Renaissance: artists develop plane Focal systematic methods to determine perspective length projection (around 1480-1515) Optical Camera axis frame ‘ Scene / world ‘’ ’ points Scene point Image coordinates Raphael Durer, 1525 Forsyth and Ponce Homogeneous coordinates Perspective Projection Matrix Is this a linear transformation? • Projection is a matrix multiplication using • no—division by z is nonlinear homogeneous coordinates: Trick: add one more coordinate: ⎡ ⎤ x ⎡ ⎤ ⎡ ⎤ ⎢ ⎥ 1 0 0 0 x ⎢ ⎥ ⎢ ⎥ y x y ⎢ ⎥ ⇒ = 0 1 0 0 y ( f ' , f ' ) ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ homogeneous image homogeneous scene z z z ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ coordinates coordinates ⎣ ⎦ ⎣ ⎦ 0 0 1 / f ' 0 z / f ' ⎣ ⎦ 1 divide by the third Converting from homogeneous coordinates coordinate to convert back to non-homogeneous coordinates Complete mapping from world points to image pixel positions? Slide by Steve Seitz Slide by Steve Seitz

Perspective projection & calibration Perspective projection & calibration • Perspective equations so far in terms of World Extrinsic: camera’s reference frame…. frame Camera frame �� World frame • Camera’s intrinsic and extrinsic parameters Intrinsic: needed to calibrate geometry. Image coordinates relative to camera �� Pixel coordinates Camera frame Camera to World to 3D 2D Perspective pixel coord. = camera coord. point point projection matrix Camera trans. matrix trans. matrix (4x1) frame (3x1) (3x4) (3x3) (4x4) Weak perspective Orthographic projection • Given camera at constant distance from scene • Approximation: treat magnification as constant • World points projected along rays parallel to • Assumes scene depth << average distance to optical access camera Image World plane points: Pinhole size / aperture Adding a lens How does the size of the aperture affect the image we’d get? object lens film Larger focal point f • A lens focuses light onto the film – Rays passing through the center are not deviated Smaller – All parallel rays converge to one point on a plane located at the focal length f Slide by Steve Seitz

Pinhole vs. lens Cameras with lenses F focal point optical center (Center Of Projection) • A lens focuses parallel rays onto a single focal point • Gather more light, while keeping focus; make pinhole perspective projection practical Human eye Thin lens Rough analogy with human visual system: Thin lens Rays entering parallel Pupil/Iris – control on one side go through amount of light Left focus Right focus focus on other, and passing through lens vice versa. Retina - contains In ideal case – all rays sensor cells, where from P imaged at P’. image is formed Fovea – highest Lens diameter d Focal length f concentration of cones Fig from Shapiro and Stockman Focus and depth of field Thin lens equation 1 1 1 = + f u v u v • Any object point satisfying this equation is in focus Image credit: cambridgeincolour.com

Focus and depth of field Focus and depth of field • How does the aperture affect the depth of field? • Depth of field: distance between image planes where blur is tolerable Thin lens: scene points at distinct depths come in focus at different image planes. (Real camera lens systems have greater depth of field.) • A smaller aperture increases the range in which the “circles of confusion” object is approximately in focus Shapiro and Stockman Flower images from Wikipedia http://en.wikipedia.org/wiki/Depth_of_field Slide from S. Seitz Depth from focus Field of view • Angular Images from same point of measure of view, different portion of 3d camera parameters space seen by the camera 3d shape / depth estimates [figs from H. Jin and P. Favaro, 2002] Images from http://en.wikipedia.org/wiki/Angle_of_view Field of view depends on focal length Field of view depends on focal length • As f gets smaller, image becomes more wide angle – more world points project onto the finite image plane • As f gets larger, image becomes more telescopic – smaller part of the world projects onto the finite image plane Smaller FOV = larger Focal Length Slide by A. Efros from R. Duraiswami

Resolution Digital cameras • sensor: size of real world scene element a that • Film � sensor array images to a single pixel • Often an array of charge • image: number of pixels coupled devices • Influences what analysis is feasible, affects best • Each CCD is light sensitive representation choice. diode that converts photons (light energy) to electrons camera CCD frame array optics computer grabber [fig from Mori et al] Digital images Digital images width 520 j=1 Think of images as i=1 Intensity : [0,255] matrices taken from CCD array. 500 height im[176][201] has value 164 im[194][203] has value 37 Color sensing in digital cameras Bayer grid Color images, Estimate missing RGB color components from space neighboring values (demosaicing) R G B Source: Steve Seitz

Historical context Summary • Pinhole model: Mozi (470-390 BCE), • Image formation affected by geometry, Aristotle (384-322 BCE) photometry, and optics. • Principles of optics (including lenses): Alhacen (965-1039 CE) • Projection equations express how world points Alhacen’s notes • Camera obscura: Leonardo da Vinci mapped to 2d image. (1452-1519), Johann Zahn (1631-1707) • Homogenous coordinates allow linear system for • First photo: Joseph Nicephore Niepce (1822) projection equations. • Daguerréotypes (1839) • Photographic film (Eastman, 1889) • Lenses make pinhole model practical. • Cinema (Lumière Brothers, 1895) Niepce, “La Table Servie,” 1822 • Parameters (focal length, aperture, lens • Color Photography (Lumière Brothers, 1908) diameter,…) affect image obtained. • Television (Baird, Farnsworth, Zworykin, 1920s) • First consumer camera with CCD : Sony Mavica (1981) • First fully digital camera: Kodak DCS100 (1990) Slide credit: L. Lazebnik CCD chip Next Problem set 0 due Thursday turnin --submit harshd pset0 <filename> Thursday : Color • Read F&P Chapter 6