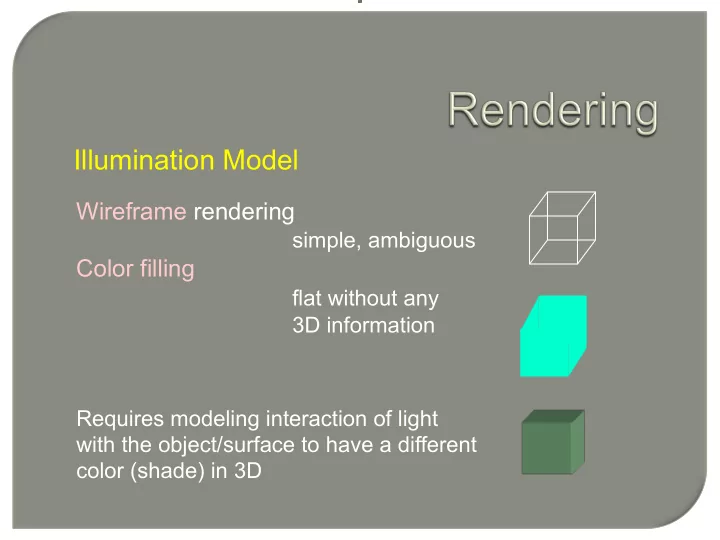
Illumination Model Wireframe rendering simple, ambiguous Color - PowerPoint PPT Presentation

Illumination Model Wireframe rendering simple, ambiguous Color filling flat without any 3D information Requires modeling interaction of light with the object/surface to have a different color (shade) in 3D

Illumination Model Light on a surface is • Absorbed • Reflected • Transmitted The amount reflected determines the color and brightness of the object light material (surface) interaction

Illumination Model The reflected light is scattered depending upon the surface properties and incident light Ambient light comes from all directions, is scattered in all directions Diffuse light comes from one direction and is scattered in all directions Specular light comes from one direction and is scattered in preferred direction

Illumination Model Diffuse Reflection Lambert ’ s Law N I α cos θ diffuse L θ I k I cos θ = d d l I k I ( L N ) = • d d l L: Light vector k d diffuse reflection coefficient N: Normal θ : Angle between L and n

Illumination Model Diffuse Reflection

Illumination Model Diffuse Reflection

Illumination Model Diffuse Reflection Amount of light reflected depends on the direction to the light source and not on the direction to the viewer Viewer independent Distance from light source q can also be incorporated I k I ( L N ) = • d d l k d I ( L N ) = • l 2 a bq cq + +

Illumination Model Specular Reflection • Highlights / Shininess • Viewing Direction

Illumination Model Specular Reflection L: Light vector R N N: Normal L θ θ α V θ : Angle between L and N α : Angle between R and V n I k I cos α = k s specular reflection coefficient s s l n I k I ( R V ) n specular reflection exponent = • s s l

Illumination Model Specular Reflection n=1 5 10 large n: metals small n: paper

Illumination Model Specular Reflection Example

Illumination Model Ambient Reflection Light from distributed light sources (and surroundings) Also approximates effects of diffusely reflected light from outer bodies / objects. k a ambient reflection coefficient I k I = ambient a a I a ambient incident light

Illumination Model Phong Illumination Model I ambient reflection diffuse reflection specular reflection = + + total n k I k I cos θ k I cos α = + + a a d l s l n k I k I ( L N ) k I ( R V ) = + • + • a a d l s l m n k I k I ( L N ) k I ( R V ) = + ∑ • + • a a d i i s i i i 1 =

Illumination Model Phong Illumination Model Local computation for obtaining color (intensity) at a point of the surface Basic inputs are light(s), material properties

Illumination Model Reflection Vector N R N 2 ( L N ) N • L L θ i θ r R -L R 2 ( L N ) N L = • −

Illumination Model Half Way Vector Instead of R • V can use N • H N H R H = L + V L V L + V

Illumination Model Normal Vector Plane ax by cz d 0 + + + = n ( p p ) 0 • − 0 = n [ a b c ] p = n Normalize p 0

Illumination Model Normal Vector Plane v 3 n ( v v ) ( v v ) = − × − 3 1 2 1 Normalize v 1 v 2

Illumination Model Normal Vector Sphere Implicit Equation 2 2 2 f ( x , y , z ) x y z 1 0 = + + − = f f f ∂ ∂ ∂ ⎡ ⎤ n , , = ⎢ ⎥ x y z ∂ ∂ ∂ ⎣ ⎦

Illumination Model Normal Vector Parametric Surface ∂ v ∂ n ∂ ∂ b m , n ( u , v ) b m , n ( u , v ) × u v ∂ ∂ n ( u , v ) ∂ = ∂ ∂ b m , n ( u , v ) b m , n ( u , v ) u × ∂ u v ∂ ∂

Illumination Model Light Sources Point light source Given by a point Light emitted in all directions Direction light source Given by a vector Spotlight light Given by a cone

Illumination Model