Hybrids: Linear Combination of S and P leads to lowering of energy - PowerPoint PPT Presentation

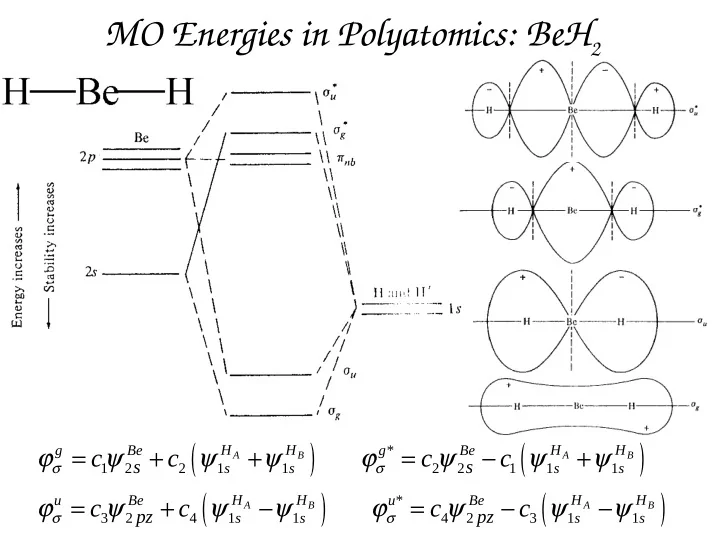
MO Energies in Polyatomics: BeH 2 ( ) ( ) ϕ = ψ + ψ + ψ ϕ = ψ − ψ + ψ g Be H H g * Be H H c c c c A B A B s s σ σ 1 2 2 1 s 1 s 2 2 1 1 s 1 s ( ) ( ) ϕ = ψ + ψ − ψ ϕ = ψ − ψ − ψ u Be H H u * Be H H c c c c A B A B pz pz σ σ 3 2 4 1 s 1 s 4 2 3 1 s 1 s

Hybrids: Linear Combination of S and P leads to lowering of energy Linus Pauling, ~1930 • Hybridization is close to VBT. Use of experimental information • All hybrid orbitals equevalent and are orthonormal to each other

Linear Environment: s & 1-p mix: sp ϕ = ψ + ψ sp c c 2 equivalent hybrid orbitals of the same s p h 1 1 2 energy and shape (directions different) ϕ = ψ − ψ sp c c S and P orbital of the s p h 2 1 2 Same atom! This is not The same as S (overlap) 1 1 ϕ = ψ + ψ sp s p h 1 2 2 1 1 ϕ = ψ − ψ sp s p h 2 2 2 Linear geometry with Hybridized atom at the center 2S- and 2P- (similar energy) Mixes to form hybrid orbital which forms a MO with H (1S) Contribution from s=0.5; contribution from p=0.5 Have to normalize each hybridized orbital

Contours & bonding of sp-hybridization 2 more p-orbital available for bonding

Trigonal Environment: Mixing s & 2-p p x and p y can be combined with s to get three 3 equivalent hybrids at 120 o to each other y y y 30 o 30 o 30 o x x x 30 o 30 o 30 o +y hy1 Θ 1 − Signs of un normalized hybrid orbitals +x ϕ ≡ ψ + θ ψ + θ ψ -x c Cos . Sin . s p p hy 1 1 1 1 x y Θ 3 ϕ ≡ ψ + θ ψ + θ ψ c Cos . Sin . hy3 s p p hy 2 1 2 2 x y Θ 2 ϕ ≡ ψ + θ ψ + θ ψ c Cos . Sin . hy2 -y s p p hy 3 1 3 3 x y

Signs of AOs for specific Sp 2 hybrid orbitals (given an orientation) +y +y +y h1 +x +x +x 30 o 30 o 30 o 30 o h3 h2 2 2 ϕ = ψ + ψ + ψ ϕ = ψ + ψ + ψ sp sp c 0. c c c c c s p p s p p h 1 1 2 3 h 1 1 2 3 x y x y 2 2 ϕ = ψ + ψ + ψ ϕ = ψ + ψ − ψ sp sp c c c c c c s p p s p p h 2 4 5 6 h 2 4 5 6 x y x y 2 2 ϕ = ψ + ψ + ψ sp ϕ = ψ − ψ − ψ sp c c c c c c s p p s p p h 2 7 8 9 h 3 7 8 9 x y x y

How to obtain coefficients for this specific geometry of Sp 2 ? 2 +y ϕ = ψ + ψ + ψ sp c 0. c c s p p h 1 1 2 3 x y h1 2 ϕ = ψ + ψ − ψ sp c c c s p p h 2 4 5 6 x y +x 2 ϕ = ψ − ψ − ψ sp c c c s p p h 3 7 8 9 30 o 30 o x y ϕ Each is normalized h3 h2 + + = 2 2 2 c c c 1 + + = 2 2 2 c c c 1 (Total s-contribution) 1 2 3 1 4 7 + + = 2 2 2 c c c 1 = = c c c (s contributes equally) 4 5 6 1 4 7 + + = 2 2 2 ϕ ϕ c c c 1 , : orthogonal = c 0 (h along x) 7 8 9 i j 2 1 P and P Coeffs . + + = c c c c c c 0 x y = c c ( symmetry ) 1 4 2 5 3 6 5 8 + + = 2 2 2 + + = c c c 1 c c c c c c 0 = c c ( symmetry ) 2 5 8 4 7 5 8 6 9 6 9 + + = + + = 2 2 2 c c c c c c 0 c c c 1 3 6 9 7 1 8 2 9 3

Signs and coefficients for these particular Sp 2 hybrids 1 2 +y 2 ϕ = ψ + ψ + ψ sp 0. s p p h 1 h1 x 3 y 3 1 1 1 2 ϕ = ψ + ψ − ψ sp s p p +x h 2 x y 3 2 6 30 o 30 o 1 1 1 2 ϕ = ψ − ψ − ψ sp s p p h 3 h3 h2 x y 3 2 6 Square of coefficients  Contribution from s=0.33; from p=0.66

Hybridization of s & 3-p:sp 3 : Tetrahedral 1 1 1 1 3 ϕ = ψ + ψ + ψ + ψ sp s p p p h 1 2 2 x 2 y 2 z 1 1 1 1 3 ϕ = ψ − ψ − ψ + ψ sp s p p h 2 p 2 2 x 2 2 z y 1 1 1 1 3 ϕ = ψ + ψ − ψ − ψ sp s p p p h 2 2 2 x 2 y 2 z 1 1 1 1 3 ϕ = ψ − ψ + ψ − ψ sp s p p p h 4 2 2 x 2 y 2 z Contributions from s = 25%; p=75% • How do we calculate the coefficients? Use orthonormality of hybrid-orbitals and symmetry arguments • There is no unique combination/solution (depends on the geometry!)

What if h1 is oriented along z-axis? 1 3 ϕ = ψ + ψ + ψ + ψ 0. 0. 3 s p p p ϕ = ψ + ψ + ψ + ψ sp h 1 c c c c 2 x y 2 z s p p p h 1 1 2 3 4 x y z 1 2 1 ϕ = ψ + ψ + ψ − ψ 0. 3 ϕ = ψ + ψ + ψ + ψ sp c c c c s p p h 2 p 2 3 x z s p p 2 3 y h 2 1 5 7 p 8 x z y 1 1 1 1 3 ϕ = ψ + ψ ψ + ψ sp c c + c c ϕ = ψ − ψ + ψ − ψ s p p p s p p p h 2 1 9 10 11 h 3 x y z 2 x y z 6 2 2 3 3 ϕ = ψ + ψ + ψ + ψ sp 1 1 1 1 c c c c ϕ = ψ − ψ − ψ − ψ s p p p h 4 1 12 13 14 x y z s p p p h 4 2 x y z 6 2 2 3