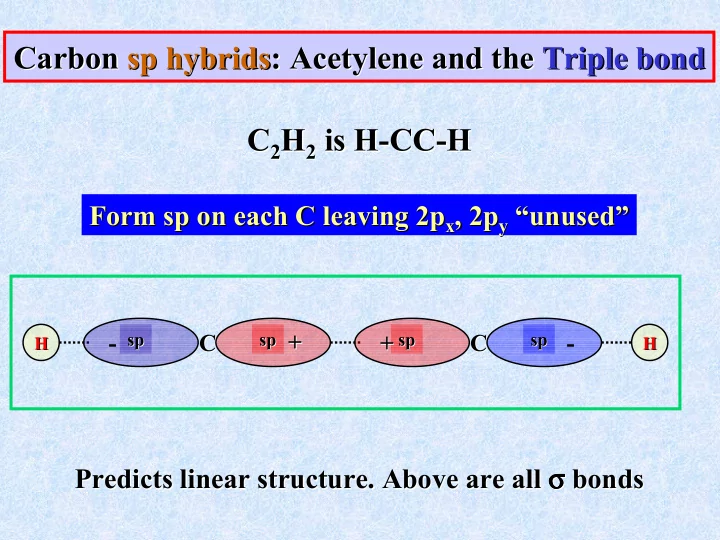
Carbon sp sp hybrids hybrids: Acetylene and the : Acetylene and - PowerPoint PPT Presentation

Carbon sp sp hybrids hybrids: Acetylene and the : Acetylene and the Triple bond Triple bond Carbon C 2 H 2 is H- -CC CC- -H H C 2 H 2 is H Form sp sp on each C leaving 2p on each C leaving 2p x , 2p y “unused” Form x , 2p y “unused” sp sp + sp sp - sp C sp + + sp C sp - C + C H H H H σ bonds σ σ σ Predicts linear structure. Above are all σ σ σ σ bonds Predicts linear structure. Above are all

H- -C C- -C C- -H H H - for each C in Uses up 2 valence e for each C in sp sp (and 2 from 1s H). (and 2 from 1s H). Uses up 2 valence e - - for each C unused. Leaves 2 valence e for each C unused. Leaves 2 valence e - 2p y 2p y 2p 2p y y Put last valence 2p x Put last valence 2p x π π orbitals π π into π π π π - into orbitals e - e sp sp formed from formed from H H H H C C C C 2p x , 2p y 2p x , 2p 2p x 2p y x

- in π - in π 2 e in π x 2 e in π y 2 e - 2 e - x y Gives two π bonds connecting carbon atoms. π bonds are at right Gives two π bonds connecting carbon atoms. π bonds are at right σ σ , 2 σ σ C bonds are now 3, one σ σ σ σ angles to each other. Total C- -C bonds are now 3, one , 2 π π angles to each other. Total C Short Comparison of Bond Order, Bond Length, Bond Energy Short Comparison of Bond Order, Bond Length, Bond Energy C- -C C C- -C C C- -C C C C C Molecule Bond Order Bond Length Bond E, Molecule Bond Order Bond Length Bond E, kcal/mole kcal/mole σ ) σ σ σ 1 (1 σ σ σ σ Ethane, C 2 H 6 ) 1.54Å 83 Ethane, C 2 H 1 (1 1.54Å 83 6 σ σ , 1 σ σ 2 (1 σ σ σ σ Ethylene, C 2 H 4 , 1 π π ) ) 1.35Å Å 125 Ethylene, C 2 H 2 (1 1.35 125 4 σ , 2 σ σ σ 3 (1 σ σ σ σ Acetylene, C 2 H 2 , 2 π π ) ) 1.21Å Å 230 Acetylene, C 2 H 3 (1 1.21 230 2

Conjugation and Delocalization Delocalization of of Conjugation and Electrons and Bonds Electrons and Bonds Although energy of π * in ethylene < σ σ σ * , conjugated polylenes σ have even lower energy π * levels. These absorb light at longer wavelength- sometimes even in visible (human eye’s light perception). Conjugated polyenes: C=C-C-C=C-C 2 essentially independent double bonds. C=C-C=C-C=C polyene Double bonds ALTERNATE! Double bonds ALTERNATE!

π bonds between any 2 C’s π π π Could draw π π π π bonds between any 2 C’s Could draw π * π π π π π π π * bonds bonds C C C C C C C C C C C C drawn are drawn are not unique! not unique! ψ ψ MO ψ ψ ψ ψ ψ ψ = (Const Const)[2p )[2p y (1) + 2p y (2) MO = ( y (1) + 2p y (2) This gives delocalized delocalized structure structure This gives + 2p y (3) + 2p y (4) +2p y (5) + 2p y (3) + 2p y (4) +2p y (5) + 2p y (6) +………]. Add 2p y + 2p y (6) +………]. Add 2p y Atomic Orbitals Orbitals on each C on each C Atomic C C C C C C C C C C C C Delocalized Molecular Molecular Delocalized Orbital spans many atoms Orbital spans many atoms Delocalizing electrons generally lowers their energy. electrons generally lowers their energy. Delocalizing

π π States in the 4 Carbon π π π π π π States in the 4 Carbon Polyene Polyene Butadiene Butadiene Energy Energy π π π π * antibonding H 2 C=CH- -HC=CH HC=CH 2 H 2 C=CH 2 levels E=h ν ν ν ν (photon) 2p orbitals (one each on 4 carbons) π π π bonding π levels ν ν ν ν for butadiene << E=h ν ν for ethylene ν ν E=h ν ν ν ν for butadiene << E=h ν ν ν ν for ethylene E=h Molecular Molecular Orbital Energies Orbital Energies Delocalized π π Bonding π π π π π π 4 Delocalized Bonding 4 States Constructed C C C C States Constructed From 4 2py From 4 2py C atomic orbs C atomic orbs

Benzene C C 6 H 6 . This is a planar planar closed ring compound of closed ring compound of Benzene 6 H 6 . This is a 2 carbon hybrids: carbon which has sp sp 2 carbon hybrids: carbon which has H H H H Electron Electron C C 120 ˚ 120 ˚ Delocalization Delocalization in Carbon in Carbon sp 2 2 H C sp C H H H Ring Ring Compounds Compounds C C H H H H - in sp 2 hybrid bond structure Each C uses 3 of 4 valence e in sp 2 hybrid bond structure Each C uses 3 of 4 valence e - to make 1 C- -H bond 2 C H bond 2 C- -C bonds. C bonds. to make 1 C

- and a 2p orbital for each C Are left with 1 valence e - and a 2p orbital for each C Are left with 1 valence e π π π π π π π π or or π bonds in two different ways. Called two π π π Can make 3 π π π π bonds in two different ways. Called two resonance resonance Can make 3 structures. System alternates between the two different forms. System alternates between the two different forms. structures. This is localized picture! This is localized localized picture! picture! This is

Benzene C C 6 H 6 planar Benzene 6 H 6 planar Delocalized Picture Picture Delocalized closed ring compound closed ring compound 2 carbon hybrids with sp sp 2 carbon hybrids with H H H H leaves 6 valence electrons leaves 6 valence electrons + + and 6 p orbitals orbitals unused unused and 6 p – – – – + + H H H H – – – – π π bonds with π π Can form π π π π + + bonds with Can form – – – – these p orbitals orbitals. . these p H H H H ψ MO ψ ψ ψ ψ ψ ψ ψ = (Const Const)[2p )[2p y (1) + 2p y (2) MO = ( y (1) + 2p y (2) + 2p y (3) + 2p y (4) +2p y (5) + 2p y (3) + 2p y (4) +2p y (5) π π π bonds π these π π π π However,these bonds However, + 2p y (6)] + 2p y (6)] have the ability to delocalize delocalize have the ability to Add 6 6 2p 2p y Atomic Add y Atomic Orbitals on each C on each C Orbitals around the entire around the entire ring of 6 carbons ring of 6 carbons There are 6 such combinations! There are 6 such combinations!

Can therefore think of Can therefore think of electrons as delocalized delocalized electrons as ψ ψ MO ψ ψ ψ ψ ψ ψ = (Const Const)[2p )[2p y (1) + 2p y (2) MO = ( y (1) + 2p y (2) + 2p y (3) + 2p y (4) +2p y (5) + 2p y (3) + 2p y (4) +2p y (5) + 2p y (6)] + 2p y (6)] Add 6 6 2p 2p y Atomic Add y Atomic Orbitals on each C on each C Orbitals And often see And often see symbol for C 6 H 6 as symbol for C 6 H 6 as

Circle indicates this delocalization. This delocalized orbital comes from adding all 2p orbitals in phase ( + on top) and ( - on bottom). Can actually form a total of 6 delocalized M.O.’s for benzene (6 2p Atomic Orbital’s → → 6 M.O.’s). → → → → → → Beginnings Beginnings of a “conduction” of a “conduction” Energy Energy ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ band band + + Antibonding orbitals Antibonding orbitals “Band “Band ← ← ← ← 0 (isolated C 2p) ← ← 0 (isolated C 2p) ← ← π 2 π 3 π π Gap” Gap” b b b b 2 3 Bonding orbitals orbitals Bonding _ _ π 1 π b b ↑ Beginnings ↑ ↑ ↑ ↑ ↑ ↑ ↑ Beginnings 1 of a “valence” band of a “valence” band

Energy of 3 π bonding orbitals lower than energy of 2p (isolated) orbitals on C from which they come. π antibonding are higher than isolated 2p. When put 6 e - into delocalized orbital get ~ (1/2) π bond per C-C pair (1e - in π ). Each C-C pair has one σ σ σ and (1/2) π . σ Find experimentally all C-C bonds are of equal length (1.390Å) and between that of C-C bond and C=C σ σ σ σ , π bond lengths. If now consider bond energy of benzene, might guess it equals 6 C-C sigma bonds, 6 C-H sigma bonds, and 3 (C-C) π bonds.

Actually find benzene is more more stable than this! stable than this! Actually find benzene is - over 6 Delocalization of of e over 6 orbitals orbitals gives set gives set Delocalization e - of 3 M.O.’s which have lower energy than of 3 M.O.’s which have lower energy than → → → → i.e. → → → → 3 π C- -C bonds on ethylene. C bonds on ethylene. i.e. 3 π C 2 + ( π 2 + ( π 2 < Energy of 3 π Energy of ( π 1 b ) ) 2 + ( π 2 b ) ) 2 + ( π 3 b ) ) 2 < Energy of 3 π 2 2 Energy of ( π 1b 2b 3b ethylene ethylene Difference is ~ 160 kjoules kjoules/mole. This turns out to be about the /mole. This turns out to be about the Difference is ~ 160 energy of one whole ethylene π bond. energy of one whole ethylene π bond. 2 ≅ 4 π 2 + ( π 2 + ( π Energy of 4 ≅ ≅ ≅ ≅ Energy of ≅ ≅ ≅ i.e. Energy of ( π 1 1b b ) ) 2 + ( π 2 2b b ) ) 2 + ( π 3 3b b ) ) 2 π 2 2 i.e. Energy of ( π eth. eth.

b ) 2 ≅ b ) 2 = ( π 3 ≅ π 2 ≅ ≅ More accurately: Energy of ( π 2 eth b ) 2 ≅ ≅ 2 π 2 ≅ ≅ And: Energy of ( π 1 eth Beginnings Beginnings of a “conduction” of a “conduction” Energy Energy ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ band band + + Antibonding orbitals Antibonding orbitals “Band “Band ← ← ← ← 0 (isolated C 2p) ← ← 0 (isolated C 2p) ← ← Gap” Gap” π 2 π 3 π ∆ ∆ E π 2 ∆ ∆ ∆ ∆ ∆ ∆ E Eth 2 2b b 3b b Eth _ _ Bonding orbitals orbitals Bonding π 1 π b b ↑ ↑ Beginnings ↑ ↑ ↑ ↑ ↑ ↑ Beginnings 1 of a “valence” band of a “valence” band