How do you visualize a coordinate system? Do you think of this? z - PowerPoint PPT Presentation

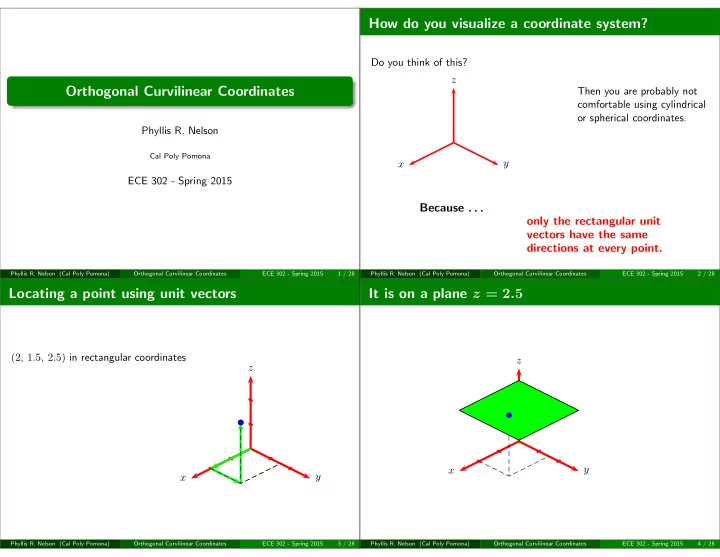
b b How do you visualize a coordinate system? Do you think of this? z Orthogonal Curvilinear Coordinates Then you are probably not comfortable using cylindrical or spherical coordinates. Phyllis R. Nelson Cal Poly Pomona y x ECE 302 - Spring 2015 Because . . . only the rectangular unit vectors have the same directions at every point. Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 1 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 2 / 28 Locating a point using unit vectors It is on a plane z = 2 . 5 (2 , 1 . 5 , 2 . 5) in rectangular coordinates z z y x y x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 3 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 4 / 28

b b b . . . a plane x = 2 . . . and a plane y = 1 . 5 z z y x y x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 5 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 6 / 28 Start with surfaces, not unit vectors! Find the unit vectors at a point from the surfaces. z ˆ Points can be specified by three surfaces with equations of the form z = 2 . 5 f 1 ( x, y, z ) = q 1 y ˆ x ˆ f 2 ( x, y, z ) = q 2 x = 2 f 3 ( x, y, z ) = q 3 y = 1 . 5 where the numbers q i are the coordinates of the point. The unit vectors at the point are normal to the surfaces point toward increasing q . Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 7 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 8 / 28

Cylindrical coordinates Spherical coordinates x 2 + y 2 + z 2 � � x 2 + y 2 f 1 = r = f 1 = ρ = f 2 = θ = cos − 1 ( z/r ) f 2 = φ = tan − 1 ( y/x ) z z f 3 = φ = tan − 1 ( y/x ) f 3 = z Unit vectors: Unit vectors: ρ ˆ ˆ r y y x ˆ x ˆ φ θ ˆ φ z ˆ Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 9 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 10 / 28 Finding � Generalized curvilinear coordinates dl in rectangular coordinates What is the distance between the surfaces f i = q i and f i = q i + dq i ? Function Coordinate Unit Vector . . . between the surfaces x = x 0 and x = x 0 + dx ? f 1 q 1 u ˆ . . . between the surfaces y = y 0 and y = y 0 + dy ? f 2 q 2 ˆ v . . . between the surfaces z = z 0 and z = z 0 + dz ? f 3 q 3 w ˆ � dl = ˆ x dx + ˆ y dy + ˆ z dz Orthogonal curvilinear coordinates: surfaces of constant f i must everywhere be mutually orthogonal. z Right-handedness: u × ˆ ˆ v = ˆ w OLC Rectangular Cylindrical Spherical f 1 x ρ r f 2 y φ θ f 3 z z φ y x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 11 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 12 / 28

Finding � Finding � dl in cylindrical coordinates dl in spherical coordinates What is the distance between the surfaces ρ = ρ 0 and ρ = ρ 0 + dρ ? What is the distance between the surfaces r = r 0 and r = r 0 + dr ? . . . between the surfaces φ = φ 0 and φ = φ 0 + dφ ? . . . between the surfaces θ = θ 0 and θ = θ 0 + dθ ? . . . between the surfaces φ = φ 0 and φ = φ 0 + dφ ? . . . between the surfaces z = z 0 and z = z 0 + dz ? � +ˆ � +ˆ +ˆ dl = ˆ ρ φ +ˆ z dz dl = ˆ r θ φ z z y x y x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 13 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 14 / 28 Finding � dl : summary Differential area in cylindrical coordinates z � dl = ˆ u h 1 dq 1 + ˆ v h 2 dq 2 + ˆ u h 3 dq 3 ρ dz OLC Rectangular Cylindrical Spherical ρ dφ h 1 1 1 1 y h 2 1 ρ r x h 3 1 1 r sin θ Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 15 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 16 / 28

b b Differential volume in spherical coordinates Converting unit vectors Example: rectangular to cylindrical � ρ dρ + ˆ z dl = ˆ φ ρdφ + ˆ z dz = ˆ x dx + ˆ y dy + ˆ z dz � ∂x ∂ρdρ + ∂x � � ∂y ∂ρdρ + ∂y � = ˆ x ∂φdφ + ˆ y ∂φdφ + ˆ z dz � � � � = dρ + ρ dφ + ˆ z dz dr rdθ r sin θ dφ ∂x ∂x y x = ρ cos φ ∂ρ = ∂φ = x ∂y ∂y y = ρ sin φ ∂ρ = ∂φ = ˆ ρ = ˆ φ = Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 17 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 18 / 28 y Gradient of a scalar field ˆ ρ y sin φ ˆ Given a scalar field S ( q 1 , q 2 , q 3 ) , x cos φ ˆ ρ dS = ∂S dq 1 + ∂S dq 2 + ∂S dq 3 = � ∇ S · � dl ∂q 1 ∂q 2 ∂q 3 φ x � dl = ˆ u h 1 dq 1 + ˆ v h 2 dq 2 + ˆ w h 3 dq 3 y ˆ φ ˆ y cos φ ρ − ˆ x sin φ � ∇ S = φ x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 19 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 20 / 28

b Direction of the gradient of a scalar field Divergence of a vector field h = x 2 y x 2 * y 12 10 8 6 30 4 20 2 10 0 Given a vector field -2 0 -4 -10 -6 -20 -8 -30 -10 � -12 V ( q 1 , q 2 , q 3 ) = uV 1 ( q 1 , q 2 , q 3 ) + ˆ ˆ v V 2 ( q 1 , q 2 , q 3 ) + ˆ w V 3 ( q 1 , q 2 , q 3 ) 3 2 1 dS = � ∇ S · � dl = | � ∇ S | | � -3 0 dl | cos α -2 y -1 -1 0 -2 1 x 2 3-3 dS 3 = | � � ∂ ∇ S | cos α 1 ( V 1 h 2 h 3 ) + ∂ ( V 2 h 3 h 1 ) + ∂ � | � 2 dl | ∇ · � � V = ( V 3 h 1 h 2 ) h 1 h 2 h 3 ∂q 1 ∂q 2 ∂q 3 1 0 y -1 -2 -3 -3 -2 -1 0 1 2 3 x Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 21 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 22 / 28 ρ ρ 2 (vector plot) � Meaning of the divergence V = ˆ 3 Let � x f ( x ) , � x dy dz , and � V = ˆ dσ + = ˆ dσ − = − ˆ x dy dz 2 � � V · � � x = x 0 + � V · � dσ + dσ − x = x 0 + dx = � � � � 1 z 0 dy � ∂f � = ( dx dy dz ) dz -1 ∂x � dσ − � dσ + -2 x y x 0 dx -3 -3 -2 -1 0 1 2 3 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 23 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 24 / 28

ρ ρ 2 (3-D surface plot) Divergence of � V = ˆ Curl of a vector field ∇ · � � V = Divergence Let � 12 V = ˆ u V 1 + ˆ v V 2 + ˆ w V 3 . 8 4 14 12 � � h 1 ˆ u h 2 ˆ v h 3 ˆ w 10 � � 1 8 � � ∇ × � � ∂ ∂ ∂ V = � � 6 ∂q 1 ∂q 2 ∂q 3 h 1 h 2 h 3 � � 4 � � h 1 V 1 h 2 V 2 h 3 V 3 2 � � 0 3 2 1 -3 0 -2 y -1 -1 0 -2 1 x 2 3-3 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 25 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 26 / 28 Vector 2 nd derivatives V = ˆ � φ ( − ρ ) (vector plot) ρ ˆ � � 3 ˆ ρ φ z ˆ � � V = 1 ∇ · ( � � � = ∇ 2 S (Laplacian) ∇ S : ∇ S ) ∇ × � � � � ∂ρ ∂φ ∂z � � ρ ∇ × ( � � 2 � � ∇ S ) = 0 0 ρ ( − ρ ) 0 � � 1 ∇ · � � ∇ ( � � ∇ · � � = ∇ 2 � V : V ) V (!!!) ∇ × ( � � ∇ · � V ) = 0 0 y -1 ∇ × � � ∇ · ( � � ∇ × � V : V ) = 0 V = ˆ � φ ( − ρ ) = ˆ x y − ˆ y x � � � � � ∇ × � � = � ∇ · � � − ∇ 2 � ∇ × V ∇ V V -2 -3 -3 -2 -1 0 1 2 3 x The last equation above defines ∇ 2 � ∇ × � � V , the Laplacian of a vector. V = ˆ z ( − 2) Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 27 / 28 Phyllis R. Nelson (Cal Poly Pomona) Orthogonal Curvilinear Coordinates ECE 302 - Spring 2015 28 / 28