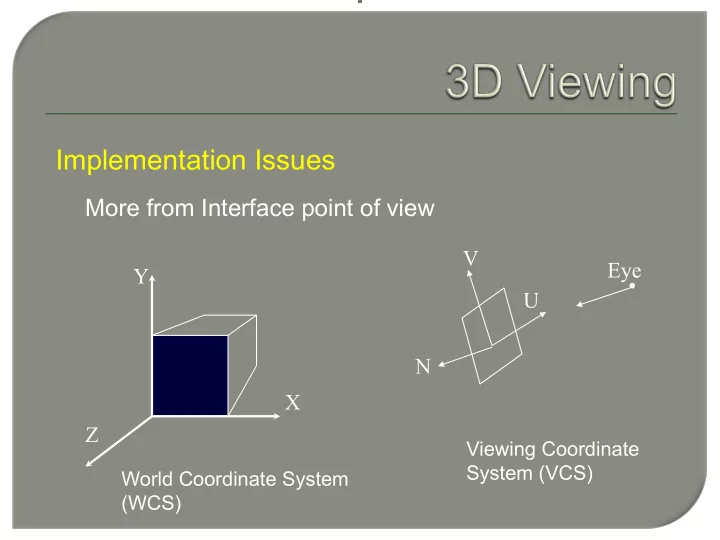
Implementation Issues More from Interface point of view V Eye Y - PowerPoint PPT Presentation

Implementation Issues More from Interface point of view V Eye Y U N X Z Viewing Coordinate System (VCS) World Coordinate System (WCS)

View Coordinate System (VCS) Viewing coordinate system • Position and orientation of the view plane • Extent of the view plane (window) • Position of the eye View Plane • View Reference Point (VRP): the origin of VCS specified as (r x , r y , r z ) in WCS: center of the scene • Normal to the view plane (n x , n y , n z )

View Coordinate System (VCS) View Plane • Normal Direction (View Plane Normal VPN) n (n x ,n y ,n z ) Z User may provide normalized vector e.g. φ n x = sin φ cos θ r Y n y = sin φ sin θ X θ n z = cos φ

View Coordinate System (VCS) View Plane • Direction v v is a unit vector intuitively corresponding to “ up ” vector “ up ” vector is specified by the user in WCS up ’ = up – (up.n)n up ’ up v = up ’ / |up ’ | n v • Direction u u = n x v ( Left Handed)

View Coordinate System (VCS) Window and Eye • Window : left, right, bottom,top (w l ,w r ,w b ,w t ) w r w t generally is centered at VRP (origin) • Eye : e = (e u ,e v ,e n ) Typically e = (0,0,-E) n v u e w l w b

Transformation from WCS to VCS v Y (x, y) O ’ u ⎛ ⎞ ( x y ) ( a b ) r = ⎜ ⎟ + v ⎝ ⎠ u r ( a b ) M r = + O X

Transformation from WCS to VCS Point object is represented as • (a,b,c) in VCS • (x,y,z) in WCS u u u u ⎡ ⎤ ⎡ ⎤ x y z ⎢ ⎥ ⎢ ⎥ M v v v v = = x y z ⎢ ⎥ ⎢ ⎥ n n n n ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ x y z ⎦

Transformation from WCS to VCS Conversion from one coordinate system to another p [ x y z ] [ a b c ] M r = = + 1 [ ] − a b c ( p r ) M = − T ( p r ) M = − Therefore a=(p-r).u, b=(p-r).v, c=(p-r).n

Set up 3D Viewing Interface (Revisit) Conversion from one coordinate system to another • (a,b,c) in VCS • (x,y,z) in WCS p [ x y z ] [ a b c ] M r = = + 1 [ ] − a b c ( p r ) M = − u u u u ⎡ ⎤ ⎡ ⎤ x y z T ( p r ) M ⎢ ⎥ ⎢ ⎥ = − M v v v v Where = = x y z ⎢ ⎥ ⎢ ⎥ n n n n ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ x y z ⎦

Set up Steps 1. Define the view reference point (VRP) = r 2. Obtain M defining u , v , n 3. Define the position of eye (in VCS) e = ( e u , e v , e n ) typically ( 0, 0, -E ) corresponding point in WCS will be eye = ( 0, 0, -E ) M + r 4. Define the window and the pixel location.

Set up rows : 0 to MAXROW v cols : 0 to MAXCOL W t (i,j) th pixel : (u i , v j , 0) n u i = W l + i Δ u W b v j = W t – j Δ v W l u Δ u = ( W r – W l ) / MAXCOL e ( 0 ,0 , -E) W r Δ v = ( W t – W b ) / MAXROW

Set up 5. Parametric equation of ray P i,j (t) = eye + dir ij t eye = ( 0 , 0 , -E ) M + r dir ij = ( ( u i , v j , 0 ) – e) M = ( u i , v j , E ) M P ij (t) = eye + dir ij t R(t) = R o + R d t

Set up • Find intersection with object (r i ) • Find the normal at r i as r n • Find intensity at I at the point (Illumination model) • Find the pixel-color

Review Basic ray tracing (one level): ray casting Algorithm: For each pixel shoot a ray from eye (COP) Compute ray-object(s) intersection Obtain the closest intersection point ( p ) Compute normal at p Compute illumination (intensity) Set up: Obtain ray in WCS for intersection using transformations Transformation of objects: Equivalent transformation for the ray

Recursive Ray Tracing T 2 D R 2 R 1 B Eye eye-ray T 1 E C A View Plane F

Recursive Ray Tracing Eye C R 1 T 1 D R 2 T 2

Recursive Ray Tracing Different Rays Eye ray (primary ray) Reflected ray Transmitted ray Shadow ray (secondary rays)

Recursive Ray Tracing Reflected Ray Recall Reflection Vector N R N 2 ( L N ) N • L L θ i θ r R -L R 2 ( L N ) N L = • −

Recursive Ray Tracing Refracted Ray Snell ’ s Law N I θ i sin θ = η i t sin θ η t i T θ t

Recursive Ray Tracing Refracted Ray Snell ’ s Law I (cos θ ) N + N i M = sin θ i I (cos θ i ) N θ i T (sin θ ) M (cos θ ) N = − t t sin θ ( I (cos θ ) N ) + t i T (cos θ ) N = − t sin θ i M η T i T ( I (cos θ ) N ) (cos θ ) N θ t = + − i t η t

Recursive Ray Tracing Eye Obj 3 L2 Obj 1 L1 Obj 1 Obj 2

Recursive Ray Tracing Eye L1 Eye Obj 3 L2 L2 Obj 1 L1 R T Obj 1 Obj 2 Obj 3 Obj 2

Recursive Ray Tracing Eye L1 Eye Obj 3 L2 L2 Obj 1 L1 L1 L1 R T Obj 1 L2 Obj 2 L2 Obj 3 R T R Obj 2

Recursive Ray Tracing When to stop ? When ray leaves the scene When the contribution to the overall intensity is small

Recursive Ray Tracing Phong Illumination Model I ambient reflection diffuse reflection specular reflection = + + total n k I k I cos θ k I cos α = + + a a d l s l n k I k I ( L N ) k I ( R V ) = + • + • a a d l s l m n k I k I ( L N ) k I ( R V ) = + ∑ • + • a a d i i s i i i 1 =

Recursive Ray Tracing Illumination When in shadow (single light source) I ambient reflection = total k I = a a

Recursive Ray Tracing Illumination With reflection and transmission rays I ( P ) I (P) k I(P ) k (P ) = + + total local rg r tg t Global Illumination

Recursive Ray Tracing T Whitted 1980

Recursive Ray Tracing Other Example

Recursive Ray Tracing Other features • Ray tracing is an image based method (pixelization) • Sampling “ aliasing ” Jagginess Moire patterns • Anti-aliasing

Recursive Ray Tracing Anti-alising • Supersampling • More number of rays per pixel • Average the result