Half-integer thermal Hall conductance in a Kitaev spin liquid - PowerPoint PPT Presentation

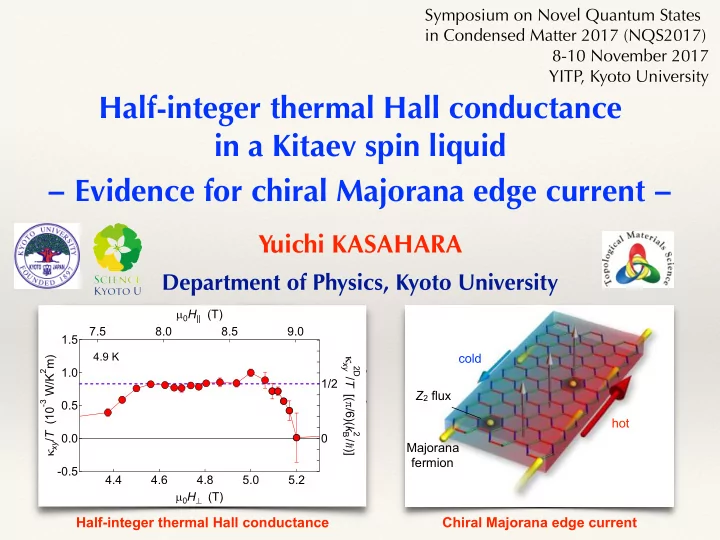
Symposium on Novel Quantum States in Condensed Matter 2017 (NQS2017) 8-10 November 2017 YITP, Kyoto University Half-integer thermal Hall conductance in a Kitaev spin liquid − Evidence for chiral Majorana edge current − Yuichi KASAHARA Department of Physics, Kyoto University µ 0 H || (T) c d 7.5 8.0 8.5 9.0 1.5 cold 4.9 K 2 m) κ xy 2D / T [( π /6)( k B 1.0 2 -3 W/K 1/2 Z 2 flux -3 0.5 κ xy / T (10 hot 2 / )] 0.0 0 Majorana h fermion -0.5 4.4 4.6 4.8 5.0 5.2 µ 0 H ⊥ (T) Half-integer thermal Hall conductance Chiral Majorana edge current

Collaborators Takafumi Onishi, Yuji Matsuda Department of Physics, Kyoto University Kaori Sugii, Masaaki Shimozawa, Minoru Yamashita Matsuda Yamashita Institute for Solid State Physics, The University of Tokyo Taka Shibauchi Department of Advanced Materials Science, The University of Tokyo Nobuyuki Kurita, Hidekazu Tanaka Shibauchi Sugii Department of Physics, Tokyo Institute of Technology Joji Nasu Department of Physics, Tokyo Institute of Technology Tanaka Shimozawa Yukitoshi Motome Department of Applied Physics, The University of Tokyo Nasu Motome

Outline 1. Introduction: Kitaev quantum spin liquid 2. A candidate of Kitaev magnet α -RuCl 3 3. Thermal Hall effect in perpendicular fields 4. Thermal Hall effect in tilted fields Observation of half-integer thermal Hall conductance 5. Summary Y. Kasahara et al ., arXiv:1709.10286 (2017).

4 Introduction Quantum spin liquid (QSL) Quantum fluctuations melt the long-range magnetic order even at T = 0 . The ground state with massive entanglement of local spins. Spin liquid are states which do not break any simple symmetry: Neither spin-rotational symmetry nor lattice translational symmetry. Platforms of QSL 1D: S = 1/2 XXZ chain 2D & 3D: Geometrically frustrated magnets 2D trianglar 2D kagome 3D pyrochlore Exotic physical properties in QSLs Topological phases Gauge fluctuations Fractionalized excitations

Kitaev model S = 1/2 spins on tri-coordinate lattices A. Kitaev, Ann. Phys. 321 , 2 (2006). X X S y i S y X S x i S x S z i S z H = − J x j − J y j − J z j <ij> x <ij> y <ij> z Kitaev Interaction Bond-dependent Ising-like interaction Exchange frustration Honeycomb lattice (2D) Hyper-honeycomb lattice (3D) A. Kitaev, Ann. Phys. 321 , 2 (2006). S. Mandal & N. Surendran, PRB 79 , 024426 (2009). − J z S z i S z − J x S x i S x j j − J x S x i S x − J y S y i S y − J y S y i S y j − J z S z i S z j j j

6 Kitaev model X X S y i S y X S x i S x S z i S z H K = − J x j − J y j − J z j Free Majorana fermions <ij> x <ij> y <ij> z on a honeycomb lattice Jordan-Wigner transformation H K = iJ x c i c j − iJ y c i c j − iJ z X X X η r c i c j η r = i ¯ c i ¯ c j Majorana 4 4 4 representation <ij> x <ij> y <ij> z A. Kitaev, Ann. Phys. 321 , 2 (2006). W p = − 1 Fractionalization of quantum spins Itinerant Majorana fermion c i Spin 1/2 S i with Dirac cone dispersion Localized Majorana fermion ¯ c i Z 2 fluxes Z 2 flux Itinerant Majorana fermion W p = η r η r 0 W p = +1 Spin fractionalization occurs below ~ J K / k B . (proximate spin liquid state) Two types of QSLs Gapped QSL : Toric code Gappless QSL : Majorana metal

7 Candidate materials Spin-orbit assisted Mott insulator with j = 1/2 4 d 5 or 5 d 5 90° bond formed by edge-shared octahedra G. Jackeli & G. Khaliullin, PRL 102 , 017205 (2006).

8 Candidate materials 2D honeycomb lattice 3D hyper-honeycomb lattice Na 2 IrO 3 β -Li 2 IrO 3 Y. Singh & P. Gegenwart, PRB 82 , 064412 (2010). α -RuCl 3 T. Takayama et al ., PRL 114 , 077202 (2015). K. W. Plumb et al. , PRB 90 , 041112 (2014).

9 Layered honeycomb magnet α -RuCl 3 [ J ~ S i · ~ S j + J K S γ i S γ i S β j + S β X j + Γ ( S α i S α H = j )] <ij> Heisenberg Kitaev off-diagonal exchange J = − 1 . 7 meV K = − 6 . 7 meV Γ = +6 . 6 meV Dominant Kitaev term J K / k B ~ 100 K K x = − 6.7 meV, K y = − 6.7 meV, K z = − 5.0 meV S. M. Winter et al ., PRB 93 , 214431 (2016). Presence of non-Kitaev interaction •AFM order with zigzag spin structure at T N ~ 7.5 K •Transition at 14 K appears due to stacking faults. J. A. Sears et al ., PRB 91 , 144420 (2015).

10 Possible signatures of Kitaev QSL in α -RuCl 3 Raman scattering Inelastic neutron scattering Experiment Theory L. J. Sandilands et al. , PRL 114 , 147201 (2015). S.-H. Do et al. , Nat. Phys. http://doi.org/10.1038/nphys4298. A. Banerjee et al ., Nat. Mater. 15 , 733 (2016). A. Banerjee et al ., Science 356 , 1055 (2017). Broad magnetic continuum appears below ~ J K / k B J. Nasu et al. , Nat. Phys. 12 , 912 (2016). Possible signature of spin fractionalization Broad magnetic continuum at high energy More direct measurements are required. Fermionic excitations

11 What gives direct signature of Majorana fermions? Effect of magnetic field ( h || [111]) A. Kitaev, Ann. Phys. 321 , 2 (2006). H = H K + H e ff h X X S y i S y X S x i S x S z i S z H K = − J x j − J y j − J z j <ij> x <ij> y <ij> z h = λ h 3 ∼ h 3 i S y H e ff h = − ˜ X S x j S z ˜ Flux gap h ∆ f ∼ 0 . 06 J K k ∆ 2 f ( ijk ) Massless Massive Non Abelian Dirac cone Dirac cone phase H = 0 H ≠ 0 Topological system characterized by Chern insulator under H Chiral edge current of Majorana fermions

12 What gives direct signature of Majorana fermions? Integer QHE Kitaev QSL Majorana electron fermion B B hot cold cold hot Z 2 flux Chiral edge current of charge neutral Chiral edge current of electrons Majorana fermions xy = ν e 2 ν : Chern number σ 2D q : Central charge κ 2D k 2 = q π xy h B = # of chiral q = v in IQHE T ~ 6 edge modes κ 2D k 2 κ 2D = ν π k 2 xy ✓ π ◆ = 1 B q = ν B xy T ~ 6 2 T 2 6 ~ Half-integer thermal Hall conductance in a Kitaev QSL

Thermal Hall effect in insulating magnets ✓ q ◆ ✓ �r T x ◆ ✓ ◆ κ xx κ xy = 0 � κ xy �r T y κ xy Magnon Hall effect Ferromagnetically ordered state arising from Berry phase Lu 2 V 2 O 7 Ho 2 V 2 O 7 , In 2 Mn 2 O 7 , BiMnO 3 Cu(1-3,bdc) Y. Onose et al , Science 329 , 297 (2010). Ideue et al ., PRB 85 , 134411 (2012). M. Hirschberger et al ., PRL 115 , 106603 (2015). Lu 2 V 2 O 7 R. Matsumoto et al ., Paramagnetic state PRB 89 , 054420 (2014). Tb 2 Ti 2 O 7 M. Hirschberger et al ., Science 348 , 106 (2015). Spin liquid state Spinon Hall effect in QSL state with spinon Fermi surface Cu 3 V 2 O 7 (OH) 2 ･ 2H 2 O ⌘ k 2 2 π 2 1 B T ⇣ ε F D. Watanabe, PNAS 113 , 8653 (2016). κ spinon = ~ τ xx 3 h d κ spinon κ spinon = ( ω c τ ) xy xx H. Katsura et al ., PRL 104 , 066403 (2010).

14 Thermal transport measurements in α -RuCl 3 Thermal Hall effect ex.) Spin liquid state: Kagome volborthite Cu 3 V 2 O 7 (OH) 2 ･ 2H 2 O spinon κ xy / T ~ 10 -5 W/K 2 m Magnetically ordered state: κ xy / T ~ 10 -5 - 10 -4 W/K 2 m Kagome Cu-(1-3,bdc) ✓ q ◆ ✓ �r T x ◆ ✓ ◆ κ xx κ xy magnon Pyrochlore Lu 2 V 2 O 7 = � κ xy �r T y 0 κ xy cf.) Phonon thermal Hall effect κ xy / T ~ 10 -6 W/K 2 m α -RuCl 3 single crystals Specific heat Magnetic susceptibility 28 • Clear anomaly at T N ~ 7.5 K 0 T Sample 1 26 • No discernible anomaly at -3 emu/mol) 24 ~ 14 K due to stacking faults 22 Sample 2 χ (10 20 High quality single crystal 18 0 5 10 15 20 T (K)

15 Longitudinal thermal conductivity κ xx 35 50 K 35 K 27 K 0.00 30 Δκ xx ( H )/ κ xx (0) 25 -0.04 20 K Sample 1 κ xx (W/Km) 0 T 20 12 T -0.08 Sample 2 Sample 2 12 K 0 T 12 15 12 T 0 4 8 12 16 8 10 µ 0 H (T) 4 T N 5 0 κ xx = κ sp xx + κ ph 0 5 10 15 T N 0 xx 0 10 20 30 40 50 60 70 spin phonon T (K) • Clear anomaly in κ xx at T N • Suppression of κ xx by magnetic field κ xx ph is usually enhanced due to suppression of spin-phonon scattering by spin polarization. Thermal transport is governed by spin excitations. Thermal Hall effect However, it is difficult to separate spin & phonon contributions.

16 Thermal Hall conductivity κ xy T > T N 12 K 2 -3 W/Km) 0 κ xy (10 7 K -2 T < T N -10 0 10 µ 0 H (T) Distinct H -dependence below and above T N • Sign change below T N • Upward curvature above T N Finite κ xy ~ 10 -2 W/Km at T < J K / k B but downward below T N e.g.) κ xy < 10 -3 W/Km in volborthite (spin liquid) Thermal Hall effect below and above T N Tb 2 Ti 2 O 7 (paramagnet) is different in origin.

17 Thermal Hall conductivity κ xy • Phonons κ xy / T ~ 10 -6 W/K 2 m π /12 8 Different T -dependence Sample 1 (6 T) A. V. Inyushkin & . N. Taldenkov, Sample 1 (12 T) 0.2 JETP Lett. 86 , 379 (2007). 6 Sample 2 (15 T) 2 m) • Magnons Finite κ xy / T usually appears -4 W/K ( κ xy 4 2D / T )/( k B in the ordered state. 0.1 κ xy / T (10 Small DM interaction 2 T N D / k B ~ 5 K << J / k B ~ 80 K 2 / h ) S. M. Winter et al ., 0 0 PRB 93 , 214431 (2016). -2 • Spin liquid with spinon Fermi surface -0.1 In volborthite, -4 Hall signal is negative. 0 20 40 60 80 κ xy / T ~ 10 -5 W/K 2 m T (K) • Enhancement of κ xy with D. Watanabe, PNAS 113 , 8653 (2006). positive sign below J K / k B ~ 80 K • Exotic quasiparticle excitations • Broad peak at ~ 20 K inherent to the spin-liquid state of α -RuCl 3 .