h x
play

h ( x ) } Although we can generally find the best set of weights - PowerPoint PPT Presentation

May 13, 2023 •174 likes •207 views

Practical Use of Linear Regression 25 25 25 20 20 20 Sales Sales Sales 15 15 15 10 10 10 5 5 5 Class #03: Linear and Polynomial Regression Models 0 50 100 200 300 0 10 20 30 40 50 0 20 40 60 80 100 TV Radio

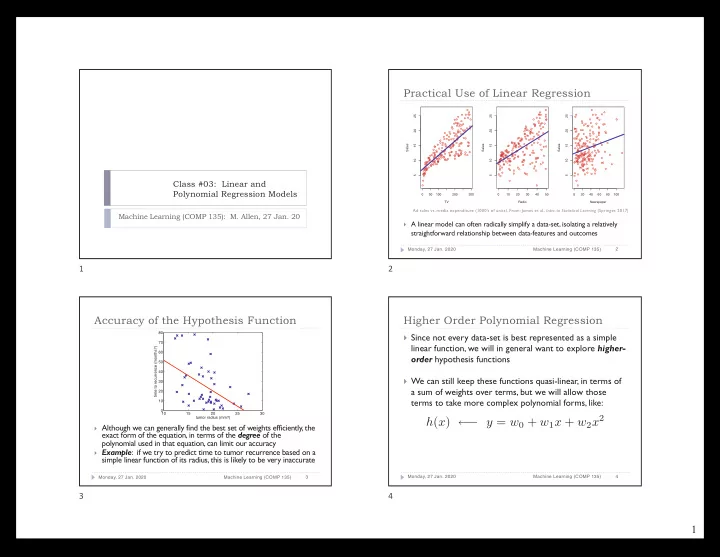
  1. Practical Use of Linear Regression 25 25 25 20 20 20 Sales Sales Sales 15 15 15 10 10 10 5 5 5 Class #03: Linear and Polynomial Regression Models 0 50 100 200 300 0 10 20 30 40 50 0 20 40 60 80 100 TV Radio Newspaper Ad sales vs. media expenditure (1000’s of units). From: James et al., Intro. to Statistical Learning (Springer, 2017) Machine Learning (COMP 135): M. Allen, 27 Jan. 20 } A linear model can often radically simplify a data-set, isolating a relatively straightforward relationship between data-features and outcomes 2 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 1 2 Accuracy of the Hypothesis Function Higher Order Polynomial Regression 80 } Since not every data-set is best represented as a simple 70 linear function, we will in general want to explore higher- time to recurrence (months?) 60 order hypothesis functions 50 40 } We can still keep these functions quasi-linear, in terms of 30 a sum of weights over terms, but we will allow those 20 terms to take more complex polynomial forms, like: 10 0 10 15 20 25 30 − y = w 0 + w 1 x + w 2 x 2 tumor radius (mm?) h ( x ) ← } Although we can generally find the best set of weights efficiently, the exact form of the equation, in terms of the degree of the polynomial used in that equation, can limit our accuracy } Example : if we try to predict time to tumor recurrence based on a simple linear function of its radius, this is likely to be very inaccurate 4 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 3 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 3 4 1

  2. Higher Order Polynomial Regression Higher-Order Regression Solutions − y = w 0 + w 1 x + w 2 x 2 h ( x ) ← } Note: the hypothesis function here is still linear, in terms of a sum of coefficients, each multiplied by a single feature y y } The same algorithms can find the coefficients that minimize error, just as before } What is different, however, are the features themselves } A feature transformation is a common ML technique x x } In order to best solve a problem, we generally don’t care what − y = 0 . 73 + 1 . 74 x + 0 . 68 x 2 h ( x ) ← − y = 1 . 05 + 1 . 60 x h ( x ) ← features we use } We will often experiment with modifying features to get better } With an order- 2 function, we can fit our data somewhat results from existing algorithms better than with the original, order- 1 version 6 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 5 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 5 6 Higher-Order Fitting Higher-Order Regression Solutions Order-3 Solution Order-4 Solution y y y y x x − y = 0 . 73 + 1 . 74 x + 0 . 68 x 2 h ( x ) ← − y = 1 . 05 + 1 . 60 x h ( x ) ← x x } It is important to note that the “curves” we get are still linear These are the result of projecting a linear structure in a higher dimensional } space back into the dimensions of the original data 8 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 7 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 7 8 2

  3. Even Higher-Order Fitting The Risk of Overfitting Order-5 Solution Order-6 Solution } An order-9 solution hits all the data points exactly, but is very “wild” at points that are y not given in the data, with y y high variance } This is a general problem for x x learning: if we over-train , we Order-7 Solution Order-8 Solution can end up with a function x that is very precise on the data we already have, but will y y not predict accurately when used on new examples x x 10 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 9 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 9 10 Defining Overfitting This Week } T o precisely understand overfitting, we distinguish between two } Linear and polynomial regression; gradient descent and types of error: gradient ascent; over-fitting and cross validation T rue error: the actual error between the hypothesis and the true 1. function that we want to learn } Readings: T raining error: the error observed on our training set of 2. examples, during the learning process } Book sections on linear methods and regression (see class schedule) } Overfitting is when: } Assignment 01: posted to class Piazza We have a choice between hypotheses, h 1 & h 2 1. We choose h 1 because it has lowest training error } Due via Gradescope, 9:00 AM, Wednesday, 29 January 2. Choosing h 2 would actually be better, since it will have lowest 3. true error, even if training error is worse } Office Hours: 237 Halligan } In general we do not know true error (would essentially need to } Mondays, 10:30 AM – Noon already know function we are trying to learn) } Tuesdays, 9:00 AM – 10:30 AM } How then can we estimate the true error? } TA hours/locations can be found on class site 12 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 11 Monday, 27 Jan. 2020 Machine Learning (COMP 135) 11 12 3

Recommend

More recommend