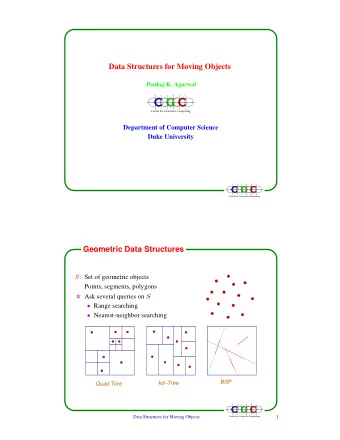
Geometric Algorithms Delaunay Triangulations and Voronoi Diagrams - PowerPoint PPT Presentation

Legal Triangulations Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔ If p, q, r, s form a convex quadrilateral and s �∈ ∂C , then either pq or rs is illegal. Def.: A triangulation without illegal edges is called legal triangulation

Legal Triangulations Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔ If p, q, r, s form a convex quadrilateral and s �∈ ∂C , then either pq or rs is illegal. Def.: A triangulation without illegal edges is called legal triangulation Are there legal triangulations?

Legal Triangulations Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔ If p, q, r, s form a convex quadrilateral and s �∈ ∂C , then either pq or rs is illegal. Def.: A triangulation without illegal edges is called legal triangulation while T has illegal edge e do flip ( T , e ) return T

Legal Triangulations Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔ If p, q, r, s form a convex quadrilateral and s �∈ ∂C , then either pq or rs is illegal. Def.: A triangulation without illegal edges is called legal triangulation while T has illegal edge e do flip ( T , e ) terminates? return T

Legal Triangulations Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔ If p, q, r, s form a convex quadrilateral and s �∈ ∂C , then either pq or rs is illegal. Def.: A triangulation without illegal edges is called legal triangulation while T has illegal edge e do flip ( T , e ) terminates, since A ( T ) increases and return T #triangulations finite

Are we stuck? We know: Every angle-optimal triangulation is legal. But is every legal triangulation angle-optimal?

. . . now for something completely different . . . Voronoi Diagrams

Motivation It is a beautiful sunny day. You know where all of the locations of ice cream parlors in town and would like to know which one is closest. How can we determine the closest ice cream parlor for every point on the map? ?

Motivation It is a beautiful sunny day. You know where all of the locations of ice cream parlors in town and would like to know which one is closest. How can we determine the closest ice cream parlor for every point on the map? ?

Motivation It is a beautiful sunny day. You know where all of the locations of ice cream parlors in town and would like to know which one is closest. How can we determine the closest ice cream parlor for every point on the map? ? !

Motivation It is a beautiful sunny day. You know where all of the locations of ice cream parlors in town and would like to know which one is closest. How can we determine the closest ice cream parlor for every point on the map? ? ! The solution is a subdivision of the plane, called Voronoi diagram. It has many applications, e.g., in geography, physics, robotics

Voronoi Diagrams Definition: The Voronoi diagram of n points { p 1 , . . . , p n } in the plane is the subdivision of the plane into n cells, such that a point q is in the cell of p i if and only if dist ( q, p i ) < dist ( q, p j ) for all i � = j .

Voronoi Diagrams long history • Descartes 1644 • Dirichlet 1850 • Voronoi 1907 Definition: The Voronoi diagram of n points { p 1 , . . . , p n } in the plane is the subdivision of the plane into n cells, such that a point q is in the cell of p i if and only if dist ( q, p i ) < dist ( q, p j ) for all i � = j .

Voronoi Diagrams for 2 points

Voronoi Diagrams for 2 points

Voronoi Diagrams for 2 points

Voronoi Diagrams for 2 points

Voronoi Diagrams for 2 points b ( p, q ) = { x ∈ R 2 : | xp | = | xq |} bisector of p and q p q

Voronoi Diagrams for 2 points = { x ∈ R 2 : | xp | = | xq |} b ( p, q ) bisector of p and q p q open half plane h ( p, q ) = { x : | xp | < | xq |}

Voronoi Diagrams for 2 points = { x ∈ R 2 : | xp | = | xq |} b ( p, q ) bisector of p and q p q open half plane open half plane h ( p, q ) h ( q, p ) = { x : | xp | < | xq |} = { x : | xq | < | xp |}

Voronoi Diagrams for n points P = { p 1 , p 2 , . . . , p n }

Voronoi Diagrams for n points

Voronoi Diagrams for n points Vor ( P ) = Voronoi diagram of P

Voronoi Diagrams Questions: 1) What are Voronoi cells, edges and vertices?

Voronoi Diagrams Questions: 1) What are Voronoi cells, edges and vertices? 2) Are Voronoi cells convex?

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P .

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell V ( { p } ) =

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell = V ( { p } ) = V ( p )

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p )

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q )

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q )

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) =

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } =

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } = ∂ V ( p ) ∩ ∂ V ( p ′ ) =

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } = � ∂ V ( p ) ∩ ∂ V ( p ′ ) � = rel-int , i.e. without endpoints

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } = � ∂ V ( p ) ∩ ∂ V ( p ′ ) � = rel-int , i.e. without endpoints

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } = � ∂ V ( p ) ∩ ∂ V ( p ′ ) � = rel-int , i.e. without endpoints • Voronoi vertex V ( { p, p ′ , p ′′ } )

Voronoi Diagrams Let P be a set of points in th plane and p, p ′ , p ′′ ∈ P . p ′ Voronoi diagram Vor ( P ) p p ′′ • Voronoi cell x ∈ R 2 : | xp | < | xq | ∀ q ∈ P \ { p } � � = V ( { p } ) = V ( p ) = � q � = p h ( p, q ) • Voronoi edge V ( { p, p ′ } ) { x : | xp | = | xp ′ | and | xp | < | xq | ∀ q � = p, p ′ } = � ∂ V ( p ) ∩ ∂ V ( p ′ ) � = rel-int , i.e. without endpoints • Voronoi vertex V ( { p, p ′ , p ′′ } ) = ∂ V ( p ) ∩ ∂ V ( p ′ ) ∩ ∂ V ( p ′′ )

Characterization Definition: Let q be a point. Define C P ( q ) as the largest disk with center q containing no points of P in its interior. q

Characterization Definition: Let q be a point. Define C P ( q ) as the largest disk with center q containing no points of P in its interior. C P ( q ) q

Characterization Definition: Let q be a point. Define C P ( q ) as the largest disk with center q containing no points of P in its interior. C P ( q ) q Obs.: • A point q is a Voronoi vertex ⇔ | C P ( q ) ∩ P | ≥ 3 , • the bisector b ( p i , p j ) defines a Voronoi edge ⇔ ∃ q ∈ b ( p i , p j ) with C P ( q ) ∩ P = { p i , p j } .

Delaunay Triangulation Let Vor( P ) be the Voronoi diagram of P . Def.: The graph G = ( P, E ) with E = { pq | V ( p ) und V ( q ) are adjacent } is called the dual graph of Vor( P ) .

Delaunay Triangulation Let Vor( P ) be the Voronoi diagram of P . Def.: The graph G = ( P, E ) with E = { pq | V ( p ) und V ( q ) are adjacent } is called the dual graph of Vor( P ) . G

Delaunay Triangulation Let Vor( P ) be the Voronoi diagram of P . Def.: The graph G = ( P, E ) with E = { pq | V ( p ) und V ( q ) are adjacent } is called the dual graph of Vor( P ) . Def.: The straight-line drawing of G is called Delaunay graph DG ( P ) . DG ( P )

Properties DG ( P ) has no crossing edges. Thm 3:

Properties DG ( P ) has no crossing edges. Thm 3: proof sketch: the bisector b ( p, q ) defines a Voronoi edge ⇔ ∃ r ∈ b ( p, q ) with C P ( r ) ∩ P = { p, q } . i.e. the edge pq is in DG ( P ) ⇔ there is an empty circle C p,q with p and q on its boundary. ⇒ pq can’t intersect another edge in V( p i ) p l p i Suppose p i p j is crossed by p k p l . Every circle with p k , p l has to contain either p i or p j . p k Contradiction. C i j p j in V( p j )

Properties DG ( P ) has no crossing edges. Thm 3: proof sketch: the bisector b ( p, q ) defines a Voronoi edge ⇔ ∃ r ∈ b ( p, q ) with C P ( r ) ∩ P = { p, q } . i.e. the edge pq is in DG ( P ) ⇔ there is an empty circle C p,q with p and q on its boundary. Obs.: A voronoi vertex v in Vor( P ) of degree k corresponds to a convex k -gon in DG ( P ) .

Properties DG ( P ) has no crossing edges. Thm 3: proof sketch: the bisector b ( p, q ) defines a Voronoi edge ⇔ ∃ r ∈ b ( p, q ) with C P ( r ) ∩ P = { p, q } . i.e. the edge pq is in DG ( P ) ⇔ there is an empty circle C p,q with p and q on its boundary. Obs.: A voronoi vertex v in Vor( P ) of degree k corresponds to a convex k -gon in DG ( P ) . If P is in general position (no 4 points on a circle), then all (inner) faces of DG ( P ) are triangles.

Properties DG ( P ) has no crossing edges. Thm 3: proof sketch: the bisector b ( p, q ) defines a Voronoi edge ⇔ ∃ r ∈ b ( p, q ) with C P ( r ) ∩ P = { p, q } . i.e. the edge pq is in DG ( P ) ⇔ there is an empty circle C p,q with p and q on its boundary. Obs.: A voronoi vertex v in Vor( P ) of degree k corresponds to a convex k -gon in DG ( P ) . If P is in general position (no 4 points on a circle), then all (inner) faces of DG ( P ) are triangles. A triangulation of DG ( P ) is called Delaunay triangulation.

Empty-Circle Property Theorem about Voronoi diagrams: • a point q is a Voronoi vertex ⇔ | C P ( q ) ∩ P | ≥ 3 , • the bisector b ( p i , p j ) defines a Voronoi edge ⇔ ∃ q ∈ b ( p i , p j ) with C P ( q ) ∩ P = { p i , p j } .

Empty-Circle Property Theorem about Voronoi diagrams: • a point q is a Voronoi vertex ⇔ | C P ( q ) ∩ P | ≥ 3 , • the bisector b ( p i , p j ) defines a Voronoi edge ⇔ ∃ q ∈ b ( p i , p j ) with C P ( q ) ∩ P = { p i , p j } . Thm 4: Let P be a set of points. • points p, q, r are vertices of the same face in DG ( P ) ⇔ circle through p, q, r is empty • edge pq is in DG ( P ) ⇔ there is an empty circle C p,q through p and q

Empty-Circle Property Theorem about Voronoi diagrams: • a point q is a Voronoi vertex ⇔ | C P ( q ) ∩ P | ≥ 3 , • the bisector b ( p i , p j ) defines a Voronoi edge ⇔ ∃ q ∈ b ( p i , p j ) with C P ( q ) ∩ P = { p i , p j } . Thm 4: Let P be a set of points. • points p, q, r are vertices of the same face in DG ( P ) ⇔ circle through p, q, r is empty • edge pq is in DG ( P ) ⇔ there is an empty circle C p,q through p and q Corollary: Let P be a set of points and T a triangulation of P . T is a Delaunay triangulation ⇔ circumcircle of every triangle is empty.

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. proof sketch: "‘ ⇐ "’ obvious, use Lemma 1: Let ∆ prq and ∆ pqs be two adjacent triangles in T and C the circumcircle of ∆ prq . Then: pq illegal s ∈ int( C ). ⇔

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. proof sketch: "‘ ⇒ "’ • suppose s in the interior of circle of pqr • let pr be the edge maximizing ∠ psr p s r q

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. proof sketch: "‘ ⇒ "’ t • suppose s in the interior of circle of pqr • let pr be the edge maximizing ∠ psr p s r q

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. proof sketch: "‘ ⇒ "’ t • suppose s in the interior of circle of pqr • let pr be the edge maximizing ∠ psr p s • consider t adjacent to p and r • s also lies in the circle of prt r q

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. proof sketch: "‘ ⇒ "’ t • suppose s in the interior of circle of pqr • let pr be the edge maximizing ∠ psr p s • consider t adjacent to p and r • s also lies in the circle of prt r Thales theorem: ∠ tsr > ∠ psr q Contradiction to choice of pr

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. Obs.: If P is in general position, then the Delaunay triangulation of P is unique.

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. Obs.: If P is in general position, then the Delaunay triangulation of P is unique. ⇒ legal triangulation unique

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. Obs.: If P is in general position, then the Delaunay triangulation of P is unique. ⇒ legal triangulation unique we know : T angle optimal ⇒ T legal

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. Obs.: If P is in general position, then the Delaunay triangulation of P is unique. ⇒ legal triangulation unique we know : T angle optimal ⇒ T legal ⇒ angle-optimal triangulation is DG ( P ) !

Legal vs Delaunay Thm 5: Let P be a set of points in R 2 . A triangulation T of P is legal if and only if T is a Delaunay triangulation. Obs.: If P is in general position, then the Delaunay triangulation of P is unique. ⇒ legal triangulation unique we know : T angle optimal ⇒ T legal ⇒ angle-optimal triangulation is DG ( P ) ! Is P not in general position, then the smallest angle in every triangulation of the "‘large"’ faces in DG ( P ) is the same. (proof uses Thales theorem)