Floyd-Warshall algorithm s t x y z t x 1 s 0 10 5 - PowerPoint PPT Presentation

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 2 6 0 2 ∞ ∞ y z (a) Xiaojuan Cai, School of Software, SJTU.

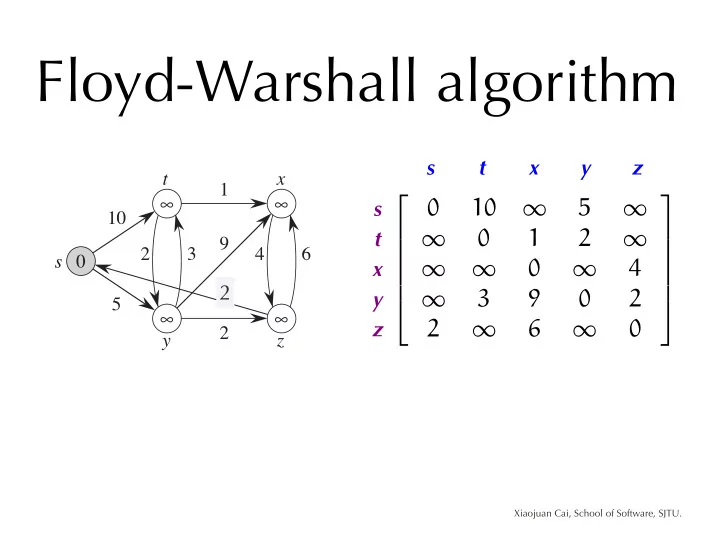
Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that passes none vertex Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15   s 0 10 5 ∞ ∞ ∞ ∞ 10 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15   s 0 10 5 ∞ ∞ ∞ ∞ 10 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15   s 0 10 5 ∞ ∞ ∞ ∞ 10 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15   s 0 10 5 ∞ ∞ ∞ ∞ 10 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t, x Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15   s 0 10 5 ∞ ∞ ∞ ∞ 10 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t, x Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15 7   s 0 10 5 ∞ ∞ ∞ ∞ 10 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t, x Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15 7   s 0 10 5 ∞ ∞ ∞ ∞ 10 4 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t, x Xiaojuan Cai, School of Software, SJTU.

Floyd-Warshall algorithm s t x y z t x 1 11 15 7   s 0 10 5 ∞ ∞ ∞ ∞ 10 4 5 t 0 1 2 ∞ ∞ 9   2 3 4 6 s 0   x 0 4 ∞ ∞ ∞   2   7 y 3 9 0 2 4 ∞ 5   ∞ ∞ z 12 7 2 6 0 10 2 ∞ ∞ y z (a) The shortest path from u to v that may passes s, t, x Xiaojuan Cai, School of Software, SJTU.