FINTE ELEMENT ANALYSIS OF THE MECHANICAL PROPERTIES OF WOVEN - PDF document

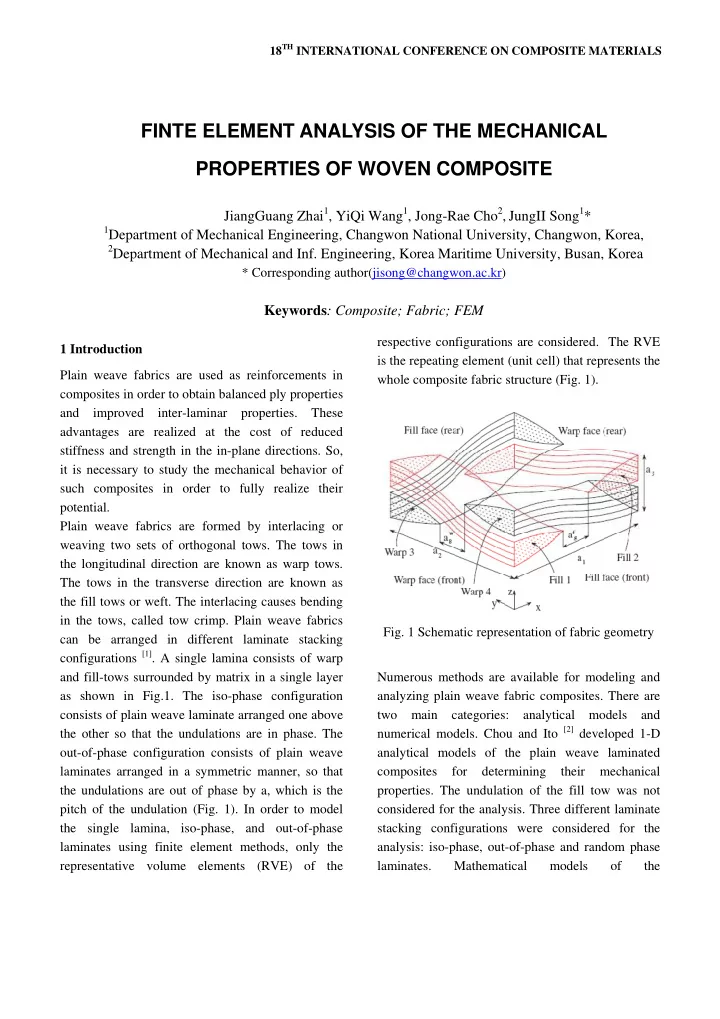
18 TH INTERNATIONAL CONFERENCE ON COMPOSITE MATERIALS FINTE ELEMENT ANALYSIS OF THE MECHANICAL PROPERTIES OF WOVEN COMPOSITE JiangGuang Zhai 1 , YiQi Wang 1 , Jong-Rae Cho 2 , JungII Song 1 * 1 Department of Mechanical Engineering, Changwon National University, Changwon, Korea, 2 Department of Mechanical and Inf. Engineering, Korea Maritime University, Busan, Korea * Corresponding author(jisong@changwon.ac.kr) Keywords : Composite; Fabric; FEM respective configurations are considered. The RVE 1 Introduction is the repeating element (unit cell) that represents the Plain weave fabrics are used as reinforcements in whole composite fabric structure (Fig. 1). composites in order to obtain balanced ply properties and improved inter-laminar properties. These advantages are realized at the cost of reduced stiffness and strength in the in-plane directions. So, it is necessary to study the mechanical behavior of such composites in order to fully realize their potential. Plain weave fabrics are formed by interlacing or weaving two sets of orthogonal tows. The tows in the longitudinal direction are known as warp tows. The tows in the transverse direction are known as the fill tows or weft. The interlacing causes bending in the tows, called tow crimp. Plain weave fabrics Fig. 1 Schematic representation of fabric geometry can be arranged in different laminate stacking configurations [1] . A single lamina consists of warp and fill-tows surrounded by matrix in a single layer Numerous methods are available for modeling and as shown in Fig.1. The iso-phase configuration analyzing plain weave fabric composites. There are consists of plain weave laminate arranged one above two main categories: analytical models and numerical models. Chou and Ito [2] developed 1-D the other so that the undulations are in phase. The out-of-phase configuration consists of plain weave analytical models of the plain weave laminated laminates arranged in a symmetric manner, so that composites for determining their mechanical the undulations are out of phase by a, which is the properties. The undulation of the fill tow was not pitch of the undulation (Fig. 1). In order to model considered for the analysis. Three different laminate the single lamina, iso-phase, and out-of-phase stacking configurations were considered for the laminates using finite element methods, only the analysis: iso-phase, out-of-phase and random phase representative volume elements (RVE) of the laminates. Mathematical models of the

c configuration ns were ex xplained ve ery well a and Th he RVE c onsists of four inter rtwined tow ws predictions o p of inplane m modulus are e compared to sur rrounded by y the matrix. . There are four volume es e experiments for all th hree config gurations. T The dep picting the t tows. Two o of them repre esent two ha alf u undulation o of warp to ow was as ssumed to be tow ws in the x-direction n (warp tow ws) and th he s inusoidal an nd two typ pes of cros ss-section w were rem maining two o represent two half to ows in the y y- assumed for a the fill tow s: sinusoidal l and elliptic cal. dir rection (fill t tows). Each volume (tow w) is modele ed The iso-strain T n condition w was used for r evaluating the as a unidirec ctional com mposite with h orthotrop ic s tiffness of th he plain weav ve laminates . pro operties in the materia l coordinate e system th hat d Chou [3,4] I shikawa and developed th hree models s to fol llows the tow w undulation n. predict the p elastic pro operties of woven fab bric model [3] was la aminates. Th he mosaic m used to pred dict th he stiffness of satin wea ave fabric c omposites. T The m model negle cts the tow w crimp and d idealizes the c composite as an assembla age of asymm metric cross- -ply la aminates. Th hen, an iso-s tress or iso-s strain condit tion Fig. 2 Photo omicrograph of the fill fa ce of fabric was used to w predict the e stiffness o of the lamin nate d depending on n whether th he laminates are assemb bled Fro om the pho tomicrograp h of the RV VE faces, th he in n series or parallel. Sin nce the mod del neglects the cur rvature of th he bounds o f the tow is so small th hat to ow crimp, th he prediction n of stiffness is not accura ate. we e could subst titute the cur rve boundary y for a straigh ht odel [3] or t The fiber un T ndulation m the 1-D mo odel lin ne, which wi ill greatly si implify the c complexity o of considers fi c iber undula ation in th he longitudi inal the e model of the unit cel l, and retain n precision o of direction but d neglects it in the transv verse directi ion. sim mulation resu ult as well. model [4] , a The bridging T combination n of mosaic a and fi fiber undulat tion model, was devel oped for sa atin weave fabric w cs. The mo odel reduces s to the cri imp model [3] for m r plain wea ave fabrics and hence the s tiffness pred diction is not t accurate. In n this studyi ing, a a straight edg ge model wa as designed t trying to sim mply th he analysis p process. Fig. 3 3- -D views of a a plain weav ve fabric 2 2 Geometric modeling 2 2.1 Finite Ele ement Mode eling Th he models w were meshe ed using 20 0 node soli id ANSYS [5] , as T The geomet tric model describing g the inter rnal ele ement of SOL LID-95 in A s shown in F ig. geometry of t g the RVE of a a single lami na is develop ped 4. The materia l properties o of the tows v vary along th he from measur fr rements take en on photom micrographs s of ori ientation of t the path line. . th he faces of f the repre sentative vo olume elem ment T h he fiber volum me fraction in the tow V V f is necessar ry (R RVE). From m photomicro ographs of t the RVE fac ces, to calculate e the to ow prope erties usin ng th he bounds o of the tow in n the fill cro oss-section a and mi icromechanic cs. Although h the tow vo olume fractio on warp cross-se w ection were almost symm metry in pla ane. is very diffic cult to mea asure directl y, it can b be

FINTE ELEMENT ANLYSIS OF THE MECHANICAL PROPERTIES OF WOVEN COMPOSITE calculated from the overall volume fraction V o and calculated from the transversely isotropic conditions. the calculated mesoscale volume fraction V g . It was These properties are checked for the restrictions on elastic constants [8] . The results are compared with [6] easily to calculate the fiber volume fraction in this model, which is 0.5. that assumes fibers to be transversely isotropic and with [6] , that uses only longitudinal fiber properties Ef1 and m12f. The results obtained from the approximate procedure show good correlation with the micromechanics model for transversely isotropic fibers. The elastic properties of the constituent materials and the overall properties of the tow (composite) are reported in Table 1. Fig. 4 Finite element model of the weave fabric Table 1 Elastic properties of the fiber and matrix of 2.2 Material Properties and Calculation of RVE Elasticity Modulus Fiber Matrix The material properties of the tows are calculated E l longit.[GPa] 221 E m [GPa] 3.4 using micromechanics [6, 7] with V 0f as fiber volume E t transv.[GPa] 16.6 v 0.35 0.26 v fraction. The elastic properties of constituent materials (fiber and matrix) for the CERL fabric are obtained from [8] and for the remaining materials from [2] . The tows are transversely isotropic and thus require only five properties (E1, E2, G12, m12, m23). Then, the properties are assigned to the tow and matrix elements in ANSYSTM. The next step is to apply the boundary conditions and analyze the results. Since AS4 carbon fiber is transversely isotropic, the elastic properties are calculated using periodic microstructure micromechanics for Fig. 5 Tensile deformation of finite element model transversely isotropic fibers [7] . As an alternative [6] to while taking into account transversely isotropic As shown in Fig.5, the Elasticity modulus in x- [9] , the following fibers with a simple model direction could be calculated by the loading a procedure is proposed. First, calculate E1 using the nonzero displacement on the face which is located at warp fiber modulus Ef1 and m12f of the fiber, and X= l w . According to the periodic boundary condition, the elastic properties of matrix. Next, calculate E2 symmetrical boundary conditions were loaded on the using the radial fiber modulus Ef2 and m12f of the faces which are located at X=0, Y=0 and Z=0. The fiber, and elastic properties of matrix. Then, nodes should be coupled together on faces which are calculate G12 using the value of G12f, m12f of the located at Y= H z and Z= l z so that the deformation fiber and elastic properties of matrix. Finally, will be in the same pattern in the faces. The total calculate G23 using Ef2, m23f of the fiber and reaction forces in x-direction on face located at X= l w elastic properties of matrix, where m23f is