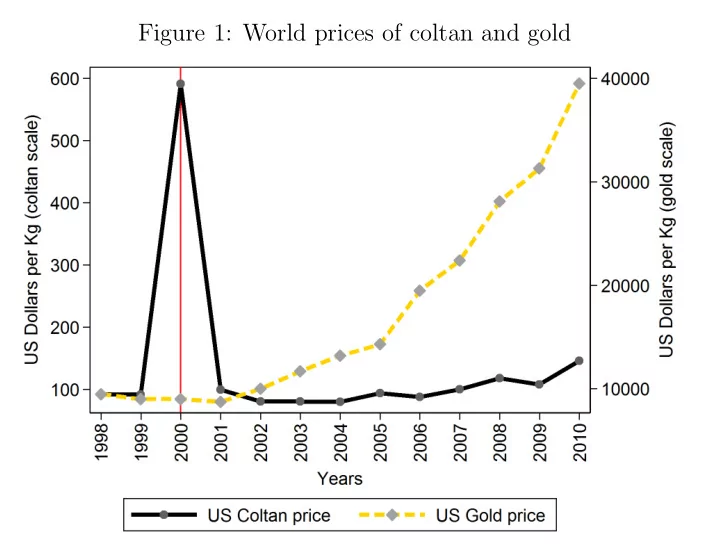
figure 1 world prices of coltan and gold figure 2 local
play

Figure 1: World prices of coltan and gold Figure 2: Local prices of - PowerPoint PPT Presentation

Mar 11, 2023 •40 likes •130 views

Figure 1: World prices of coltan and gold Figure 2: Local prices of coltan and gold Figure 6: Demand shock for coltan and presence of stationary bandits Notes : This figure plots the average number of stationary bandits on year. I take the

  1. Figure 1: World prices of coltan and gold

  2. Figure 2: Local prices of coltan and gold

  3. Figure 6: Demand shock for coltan and presence of stationary bandits Notes : This figure plots the average number of stationary bandits on year. I take the variable stationary bandit from the site survey, in which the specialists are asked to list past “organizations of security” in the site. A stationary bandit (“organization of security” in the survey) is defined as an armed actor who holds the monopoly of violence in a given site for at least 6 months (approximately). Stationary bandits most frequently are alone when they occupy a site. In some cases, multiple stationary bandits collude (this is mostly the case for the Mayi-Mayis and the FDLR in some cases), and in some, fewer cases, more than one stationary bandit may alternate in one location in a given year. The solid line graphs the average number of stationary bandits per year for mining sites that are endowed with coltan deposits, and the dashed line reports the same quantity for mining sites not endowed with coltan deposits.

  4. Table 2: Effects of price shocks, presence of stationary bandit (1) (2) (3) (4) (5) (6) (7) (8) (9) VARIABLES Coltan(i) X pc(t) 0.07** 0.10*** 0.17*** 0.21*** 0.11*** 0.20*** 0.12*** 0.13** 0.28*** (0.03) (0.03) (0.04) (0.05) (0.03) (0.03) (0.02) (0.05) (0.08) Coltan(i) X pc(t) X D road(i) -0.08 -0.07 (0.07) (0.07) pc(t) X D road(i) 0.03 0.03 (0.03) (0.04) Gold(i) X pg(t) -0.03 (0.03) Coltan(i) X pc(t) X D airport(i) -0.13** -0.10 (0.06) (0.06) pc(t) X D airport(i) 0.01 0.00 (0.02) (0.04) Coltan(i) X pc(t+1) 0.06** (0.03) Constant 0.27** 0.29*** 0.17* 0.20*** 0.27*** -0.03 0.00 41.97 91.16* (0.11) (0.06) (0.09) (0.07) (0.06) (0.10) (0.00) (46.28) (49.25) Observations 2,134 388 360 360 388 582 388 582 540 R-squared 0.68 0.87 0.87 0.88 0.88 0.76 0.79 0.82 Year FE YES YES YES YES YES YES YES YES YES Village FE YES YES YES YES YES YES YES YES YES Region*Year FE NO NO NO NO YES YES NO NO YES Arellano-Bond NO NO NO NO NO NO YES NO NO Coltan time trends NO NO NO NO NO NO NO YES YES Sample 98-08 99-00 99-00 99-00 99-00 98-00 98-00 98-00 98-00

  5. Figure 7: Effect of the price of gold on stationary bandits at gold sites, all time intervals Notes : This figure plots the estimated coefficients on gold endowment, interacted with the world price of gold, from the baseline specification using all possible time intervals. Intervals indicate 95% confidence intevals.

  6. Figure 8: Effect of the price of coltan on stationary bandits at coltan sites, all time intervals Notes : This figure plots the estimated coefficients on coltan endowment, interacted with the world price of coltan, from the baseline specification using all possible time intervals. Intervals indicate 95% confidence intevals.

  7. Figure 9: Demand shock for coltan and presence of taxation Notes : This figure plots the average number of sites where an armed actor collects taxes regularly on years. I take this variable from the site survey, in which the specialists are asked to list past taxes in the site. Taxes by an armed actor are defined in the survey as a mandatory payment on mining activity which is regular (sporadic expropriation is excluded), stable (rates of expropriation are stable) and anticipated (villagers make investment decisions with knowledge of these expropriation rates and that these will be respected). The solid line graphs the average number of mining sites where an armed actor collects regular taxes for mining sites that are endowed with available coltan deposits, and the dashed line reports the same quantity for mining sites that are not endowed with coltan deposits.

  8. Table 3: Effects of price shocks, presence of taxation (1) (2) (3) (4) (5) (6) (7) (8) (9) VARIABLES Coltan(i) X pc(t) 0.15*** 0.17*** 0.19*** 0.29*** 0.18*** 0.23*** 0.07*** 0.16*** 0.29*** (0.03) (0.04) (0.05) (0.06) (0.04) (0.03) (0.01) (0.06) (0.08) Coltan(i) X pc(t) X D road(i) -0.01 0.01 (0.08) (0.07) pc(t) X D road(i) 0.01 -0.02 (0.02) (0.03) Gold(i) X pg(t) 0.01 (0.03) Coltan(i) X pc(t) X D airport(i) -0.17** -0.22*** (0.08) (0.06) pc(t) X D airport(i) -0.00 0.07 (0.03) (0.05) Coltan(i) X pc(t+1) 0.05 (0.03) Constant -0.16 -0.11 -0.17 -0.14 -0.13 -0.36*** 0.00 -28.71 -11.57 (0.11) (0.09) (0.10) (0.09) (0.08) (0.12) (0.00) (54.65) (57.61) Observations 1,417 258 240 240 258 385 256 385 358 R-squared 0.71 0.84 0.85 0.86 0.86 0.77 0.77 0.82 Year FE YES YES YES YES YES YES YES YES YES Village FE YES YES YES YES YES YES YES YES YES Region*Year FE NO NO NO NO YES YES NO NO YES Arellano-Bond NO NO NO NO NO NO YES NO NO Coltan time trends NO NO NO NO NO NO NO YES YES Sample 98-08 99-00 99-00 99-00 99-00 98-00 98-00 98-00 98-00

  9. Table 4: Effects of price shocks by type of tax (1) (2) (3) (4) (5) (6) (7) Output Labor Poll Food Transit Mill Pillage VARIABLES Tax Tax Tax Tax Tax Tax Coltan(i) X pc(t) 0.12*** 0.07*** 0.10*** -0.01 0.01 0.02 -0.04 (0.03) (0.02) (0.03) (0.02) (0.03) (0.02) (0.04) Constant -0.20*** -0.06 0.28*** 0.11** 0.13** 0.01 0.24*** (0.06) (0.06) (0.07) (0.05) (0.06) (0.03) (0.09) Observations 1,521 1,599 1,690 1,463 1,729 1,729 1,729 R-squared 0.60 0.72 0.56 0.61 0.59 0.72 0.12 Year FE YES YES YES YES YES YES YES Village FE YES YES YES YES YES YES YES Location MINE MINE VILLAGE MARKET VILLAGE VILLAGE VILLAGE Sample 99-00 99-00 99-00 99-00 99-00 99-00 99-00

Recommend

PANEL A: Price of coltan PANEL B: Price of gold Figure 3: Support villages in the sample Notes :

PANEL A: Price of coltan PANEL B: Price of gold Figure 3: Support villages in the sample Notes :

PANEL A: Price of coltan PANEL B: Price of gold Figure 3: Support villages in the sample Notes : This map presents the location of the support villages. Support villages with at least one coltan mine are marked with a circle and cross (red).

419 views • 8 slides
1 Figure 1. Figure 2. 2 Figure 3. Figure 4. 3 Figure 5. Figure 6. 4 Figure 7. Figure 8.

1 Figure 1. Figure 2. 2 Figure 3. Figure 4. 3 Figure 5. Figure 6. 4 Figure 7. Figure 8.

Log onto a dating website and find love! Make sure your face shows your true feelings. Youre being watched StoryFace (http://www.storyface.space/, see figure 1) is a digital creation based on the capture and recognition of facial emotions.

342 views • 5 slides
Art Docent Presentation The Figure 5 in Gold Charles Demuth (1883-1935) Dear Parents, Today,

Art Docent Presentation The Figure 5 in Gold Charles Demuth (1883-1935) Dear Parents, Today,

Art Docent Presentation The Figure 5 in Gold Charles Demuth (1883-1935) Dear Parents, Today, your child learned about the poem The Great Figure (William Carlos Williams) and the painting I Saw the Figure 5 in Gold (Charles Demuth), both shown

667 views • 3 slides
2018 Employer Health Benefits Survey Release Slides October 3, 2018 Figure 1 Figure 2 Figure

2018 Employer Health Benefits Survey Release Slides October 3, 2018 Figure 1 Figure 2 Figure

2018 Employer Health Benefits Survey Release Slides October 3, 2018 Figure 1 Figure 2 Figure 3 Figure 4 Figure 5 Figure 6 Figure 7 Figure 8 Figure 9 Figure 10 Figure 11 Figure 19 Figure 12 Figure 22 Figure 13 Figure 14 Figure 15

484 views • 29 slides
1*1 Figure 1. Original Figure 2. After Figure 3. After Figure 4. After fog_ image first

1*1 Figure 1. Original Figure 2. After Figure 3. After Figure 4. After fog_ image first

BLACK AND WHITE POSITIVE SLIDES George Agius/Frank Ventura Photography was always a popular camera. In other words there is no pastime, and with the ever increasing need to develop a negative and then availability of cameras, films and reexpose

233 views • 4 slides
Figure 1: Team Logo 2 Figure 2: AISC SSBC Event Logo [1] Figure 3: Vertical Load locations [1]

Figure 1: Team Logo 2 Figure 2: AISC SSBC Event Logo [1] Figure 3: Vertical Load locations [1]

Figure 1: Team Logo 2 Figure 2: AISC SSBC Event Logo [1] Figure 3: Vertical Load locations [1] Table 1: Load combinations [1] 3 Figure 4: Construction Site Plan for Competition [1] 4 5 1 2 6 3 7 4 8 Figure 5: Preliminary Deck Trusses

256 views • 25 slides
Figure 1c Figure 1d Figure 1g Figure 1f Supplementary Figure 1c Supplementary Figure 1g

Figure 1c Figure 1d Figure 1g Figure 1f Supplementary Figure 1c Supplementary Figure 1g

Figure 1c Figure 1d Figure 1g Figure 1f Supplementary Figure 1c Supplementary Figure 1g Figure 5e, right panels. WT+Rap WT+Rap WT Con WT Con DDX6 ESC #2 DDX6 ESC #2 WT+HBSS WT+HBSS WT+RAP WT+RAP Actin LC3 WT Con WT Con DDX6 ESC #2

281 views • 10 slides
Figure 2 . Figure 3 . Figure 4 US Nuclear Industry Is Achieving Record Levels of Performance

Figure 2 . Figure 3 . Figure 4 US Nuclear Industry Is Achieving Record Levels of Performance

Figure 2 . Figure 3 . Figure 4 US Nuclear Industry Is Achieving Record Levels of Performance (1980-2000) 90 89.6 85 Capacity Factor (%) 80 75 70 65 60 55 80 82 84 86 88 90 92 94 96 98 2000 All 103 Units Figure 5 THE

489 views • 10 slides
1 Functional group classifications Chapter 2 - Alkanes Classification of hydrocarbons: aliphatic

1 Functional group classifications Chapter 2 - Alkanes Classification of hydrocarbons: aliphatic

Atoms of ethylene sp 2 -Hybridization of carbon Figure 1.24 Figure 1.25 sp -Hybridization of carbon Acetylene is a linear molecule Figure 1.29 Figure 1.28 HO O H VSEPR - Prediction of molecular geometry CO sp 3 - Tetrahedral geometry, 4

454 views • 3 slides
Figure 4.1 Drawing hands by MC Escher Figure 1.2 The brain viewed from above, with right hemisphere

Figure 4.1 Drawing hands by MC Escher Figure 1.2 The brain viewed from above, with right hemisphere

Figure 4.1 Drawing hands by MC Escher Figure 1.2 The brain viewed from above, with right hemisphere displaced to reveal the corpus callosum Figure 1.1 Embryonic origins of the cerebral hemispheres Rolandic fissure (or central sulcus) Sylvian

547 views • 53 slides
Devil Figures What is the devil figure archetype in a story? Definition: The devil figure

Devil Figures What is the devil figure archetype in a story? Definition: The devil figure

Devil Figures What is the devil figure archetype in a story? Definition: The devil figure represents a devil incarnate. They often offer worldly goods, fame, and knowledge in exchange for souls. The figure's main purpose is to distract or

440 views • 15 slides
Plasmids are excellent cloning vectors Figure 5.21 Figure

Plasmids are excellent cloning vectors Figure 5.21 Figure

Plasmids are excellent cloning vectors Figure 5.21 Figure 11.11 Order of restriction enzyme cut sites in polylinker Ampicillin lacZ resistance Apo I - Eco RI Ban II - Sac I Acc 651 - Kpn I Ava

436 views • 21 slides
Light from the West Figure: The upper limes germanicus , s. ii CE (CC-BY-SA: source) Figure: The

Light from the West Figure: The upper limes germanicus , s. ii CE (CC-BY-SA: source) Figure: The

Light from the West Figure: The upper limes germanicus , s. ii CE (CC-BY-SA: source) Figure: The upper limes germanicus , s. ii CE (public domain: source) Figure: Invasions of the Roman Empire (CC-BY-SA: source) Figure: A leaf from the Codex

485 views • 27 slides
Determinism and Volition in Antiquity Figure: Unsourceable Internet image Free Will? Figure: The

Determinism and Volition in Antiquity Figure: Unsourceable Internet image Free Will? Figure: The

Determinism and Volition in Antiquity Figure: Unsourceable Internet image Free Will? Figure: The Matrix (YouTube link) Figure: Oliver Sacks (YouTube link) mere appearance Leucippus and Democritus: Atomism (See Edmunds, Necessity, Chance,

217 views • 17 slides
Signal Theory Figure 2.1: The four-universe paradigm. Figure 2.2: Levels of abstraction in signal

Signal Theory Figure 2.1: The four-universe paradigm. Figure 2.2: Levels of abstraction in signal

Chapter 2 Signal Theory Figure 2.1: The four-universe paradigm. Figure 2.2: Levels of abstraction in signal representation. 1 2 CHAPTER 2. SIGNAL THEORY Figure 2.3: The -neighborhood in the uniform metric. Figure 2.4: Sampling and

323 views • 13 slides
Figure 1. Location map showing the Holbrook Basin in eastern Arizona. Figure 2. Map of northern

Figure 1. Location map showing the Holbrook Basin in eastern Arizona. Figure 2. Map of northern

Figure 1. Location map showing the Holbrook Basin in eastern Arizona. Figure 2. Map of northern and central Arizona showing the general location of the Rocking Chair Ranch No. 4 well, Section 27, T.14N, R.19E. Figure 3. Annotated dual induction

584 views • 26 slides
Statistical Exploration of Climate Data Figures from Module McGuire Air Force Base Figure 1:

Statistical Exploration of Climate Data Figures from Module McGuire Air Force Base Figure 1:

Statistical Exploration of Climate Data Figures from Module McGuire Air Force Base Figure 1: Average Daily Temperature at McGuire AFB Figure 2: 1955 (blue), 2000 (red) Figure 3: Anatomy of a Boxplot Figure 4: Boxplots for Each Year

146 views • 11 slides
Microorganisms and Virulence Figure 27.13 Further exposure at local sites TOXICITY:

Microorganisms and Virulence Figure 27.13 Further exposure at local sites TOXICITY:

Microorganisms and Virulence Figure 27.13 Further exposure at local sites TOXICITY: COLONIZATION toxin effects are TISSUE and local or systemic EXPOSURE INVASION ADHERENCE GROWTH DAMAGE, through epithelium to pathogens to

428 views • 21 slides
Figure PET 1 from page 150 of Exploring the Heart of

Figure PET 1 from page 150 of Exploring the Heart of

Figure PET 1 from page 150 of Exploring the Heart of Ma2er e e + 18 F 18 O FIGURE PET 1 Illustration of positron decay. One of the protons (red) in the unstable nucleus is converted into a

159 views • 3 slides
Anatomy of a transposon Figure 14.3 Examples of some

Anatomy of a transposon Figure 14.3 Examples of some

Anatomy of a transposon Figure 14.3 Examples of some bacterial transposons Figure 14.10 Figure 10.27 IS 2 tnp Tn 5 IS 50 L IS 50 R tnp kan bleo str Composite transposons

172 views • 13 slides
The Saxons Subdued Figure: Litus saxonicum c. 380 (public domain: source) Figure: Old Saxony c.

The Saxons Subdued Figure: Litus saxonicum c. 380 (public domain: source) Figure: Old Saxony c.

The Saxons Subdued Figure: Litus saxonicum c. 380 (public domain: source) Figure: Old Saxony c. 700 (public domain: source) Figure: Frankish Empire 481814 (CC-BY-SA: source) The Conquest of Old Saxony tributary to Franks defeated 531:

95 views • 7 slides
Wh What Are We We Do Doing Here? We Were re trying to fi figure out how much to c to

Wh What Are We We Do Doing Here? We Were re trying to fi figure out how much to c to

Introduce ESPlanner Aa Aaron Stevens EC1 EC171 71, 18 18 October 2011 1 Wh What Are We We Do Doing Here? We Were re trying to fi figure out how much to c to consu onsume (C (C) a ) and nd sa save ve (S (S) e ) each year,

451 views • 15 slides
Figure 07_09 Figure 07_11 Sterner & Elser 2001 Ecological Stoichiometry organelles

Figure 07_09 Figure 07_11 Sterner & Elser 2001 Ecological Stoichiometry organelles

Figure 07_09 Figure 07_11 Sterner & Elser 2001 Ecological Stoichiometry organelles macromolecules N:P balance of different mammalian organs biotic components (where they keep N and P) (Elser et al. 1996) H 375,000,000 O

296 views • 7 slides
The Proxy Wars Figure: Satan in the Old Testament, 1 of 2 (source) Figure: Satan in the Old

The Proxy Wars Figure: Satan in the Old Testament, 1 of 2 (source) Figure: Satan in the Old

The Proxy Wars Figure: Satan in the Old Testament, 1 of 2 (source) Figure: Satan in the Old Testament, 2 of 2 (source) Satan in the Book of Job Hast not thou made a fence for him, and his house, and all his his person. (Job 1:612) that he

373 views • 12 slides

More recommend