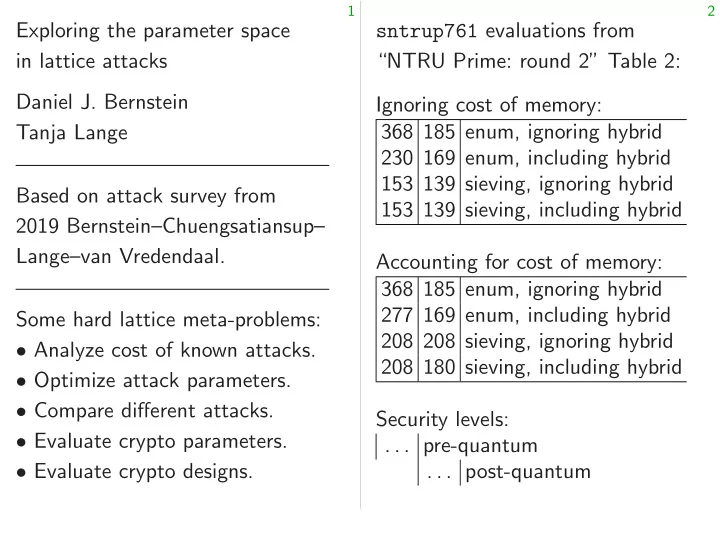

1 2 Exploring the parameter space sntrup761 evaluations from in lattice attacks “NTRU Prime: round 2” Table 2: Daniel J. Bernstein Ignoring cost of memory: 368 185 enum, ignoring hybrid Tanja Lange 230 169 enum, including hybrid 153 139 sieving, ignoring hybrid Based on attack survey from 153 139 sieving, including hybrid 2019 Bernstein–Chuengsatiansup– Lange–van Vredendaal. Accounting for cost of memory: 368 185 enum, ignoring hybrid 277 169 enum, including hybrid Some hard lattice meta-problems: 208 208 sieving, ignoring hybrid • Analyze cost of known attacks. 208 180 sieving, including hybrid • Optimize attack parameters. • Compare different attacks. Security levels: • Evaluate crypto parameters. . . . pre-quantum • Evaluate crypto designs. . . . post-quantum
1 2 ring the parameter space sntrup761 evaluations from Analysis lattice attacks “NTRU Prime: round 2” Table 2: has complications and at inte J. Bernstein Ignoring cost of memory: This talk 368 185 enum, ignoring hybrid Lange 230 169 enum, including hybrid 153 139 sieving, ignoring hybrid on attack survey from to 153 139 sieving, including hybrid Bernstein–Chuengsatiansup– Lange–van Vredendaal. Accounting for cost of memory: “App 368 185 enum, ignoring hybrid 277 169 enum, including hybrid hard lattice meta-problems: 208 208 sieving, ignoring hybrid Analyze cost of known attacks. 208 180 sieving, including hybrid Optimize attack parameters. Compare different attacks. Security levels: Mo Evaluate crypto parameters. . . . pre-quantum Evaluate crypto designs. . . . post-quantum
� � � � � 1 2 rameter space sntrup761 evaluations from Analysis of typical attacks “NTRU Prime: round 2” Table 2: has complications and at interfaces b Bernstein Ignoring cost of memory: This talk emphasizes 368 185 enum, ignoring hybrid 230 169 enum, including hybrid Analysis of 153 139 sieving, ignoring hybrid survey from to attack cryptosystems 153 139 sieving, including hybrid Bernstein–Chuengsatiansup– redendaal. Accounting for cost of memory: “Approximate-SVP” analysis 368 185 enum, ignoring hybrid 277 169 enum, including hybrid lattice meta-problems: 208 208 sieving, ignoring hybrid of known attacks. “SVP” 208 180 sieving, including hybrid analysis attack parameters. erent attacks. Security levels: Model of computation crypto parameters. . . . pre-quantum crypto designs. . . . post-quantum
� � � � � 1 2 space sntrup761 evaluations from Analysis of typical lattice attack “NTRU Prime: round 2” Table 2: has complications at four lay and at interfaces between lay Ignoring cost of memory: This talk emphasizes top lay 368 185 enum, ignoring hybrid 230 169 enum, including hybrid Analysis of lattices 153 139 sieving, ignoring hybrid from to attack cryptosystems 153 139 sieving, including hybrid Bernstein–Chuengsatiansup– Accounting for cost of memory: “Approximate-SVP” analysis 368 185 enum, ignoring hybrid 277 169 enum, including hybrid roblems: 208 208 sieving, ignoring hybrid attacks. “SVP” 208 180 sieving, including hybrid analysis rameters. attacks. Security levels: Model of computation rameters. . . . pre-quantum . . . post-quantum
� � � � � 2 3 sntrup761 evaluations from Analysis of typical lattice attack “NTRU Prime: round 2” Table 2: has complications at four layers, and at interfaces between layers. Ignoring cost of memory: This talk emphasizes top layer. 368 185 enum, ignoring hybrid 230 169 enum, including hybrid Analysis of lattices 153 139 sieving, ignoring hybrid to attack cryptosystems 153 139 sieving, including hybrid Accounting for cost of memory: “Approximate-SVP” analysis 368 185 enum, ignoring hybrid 277 169 enum, including hybrid 208 208 sieving, ignoring hybrid “SVP” 208 180 sieving, including hybrid analysis Security levels: Model of computation . . . pre-quantum . . . post-quantum
� � � � � 2 3 sntrup761 evaluations from Analysis of typical lattice attack Three typical “NTRU Prime: round 2” Table 2: has complications at four layers, Define R and at interfaces between layers. ring cost of memory: “small” = This talk emphasizes top layer. 185 enum, ignoring hybrid w = 286; 169 enum, including hybrid Analysis of lattices Attacker 139 sieving, ignoring hybrid to attack cryptosystems small weight- 139 sieving, including hybrid Problem Accounting for cost of memory: “Approximate-SVP” aG + e = analysis 185 enum, ignoring hybrid 169 enum, including hybrid Problem 208 sieving, ignoring hybrid “SVP” aG + e = 180 sieving, including hybrid analysis Problem Security levels: Public aG Model of computation re-quantum Small secrets . . post-quantum
� � � � � 2 3 evaluations from Analysis of typical lattice attack Three typical attack round 2” Table 2: has complications at four layers, Define R = Z [ x ] = ( and at interfaces between layers. memory: “small” = all coeffs This talk emphasizes top layer. ignoring hybrid w = 286; q = 4591. including hybrid Analysis of lattices Attacker wants to sieving, ignoring hybrid to attack cryptosystems small weight- w secret sieving, including hybrid Problem 1: Public cost of memory: “Approximate-SVP” aG + e = 0. Small analysis ignoring hybrid including hybrid Problem 2: Public sieving, ignoring hybrid “SVP” aG + e = A . Small sieving, including hybrid analysis Problem 3: Public Public aG 1 + e 1 ; aG Model of computation re-quantum Small secrets e 1 ; e 2 ost-quantum
� � � � � 2 3 from Analysis of typical lattice attack Three typical attack problems able 2: has complications at four layers, Define R = Z [ x ] = ( x 761 − x − and at interfaces between layers. “small” = all coeffs in {− 1 ; This talk emphasizes top layer. hybrid w = 286; q = 4591. hybrid Analysis of lattices Attacker wants to find hybrid to attack cryptosystems small weight- w secret a ∈ R including hybrid Problem 1: Public G ∈ R =q mory: “Approximate-SVP” aG + e = 0. Small secret e ∈ analysis hybrid hybrid Problem 2: Public G ∈ R =q hybrid “SVP” aG + e = A . Small secret e including hybrid analysis Problem 3: Public G 1 ; G 2 ∈ Public aG 1 + e 1 ; aG 2 + e 2 . Model of computation Small secrets e 1 ; e 2 ∈ R .
� � � � � 3 4 Analysis of typical lattice attack Three typical attack problems has complications at four layers, Define R = Z [ x ] = ( x 761 − x − 1); and at interfaces between layers. “small” = all coeffs in {− 1 ; 0 ; 1 } ; This talk emphasizes top layer. w = 286; q = 4591. Analysis of lattices Attacker wants to find to attack cryptosystems small weight- w secret a ∈ R . Problem 1: Public G ∈ R =q with “Approximate-SVP” aG + e = 0. Small secret e ∈ R . analysis Problem 2: Public G ∈ R =q and “SVP” aG + e = A . Small secret e ∈ R . analysis Problem 3: Public G 1 ; G 2 ∈ R =q . Public aG 1 + e 1 ; aG 2 + e 2 . Model of computation Small secrets e 1 ; e 2 ∈ R .
� � � � � 3 4 Analysis of typical lattice attack Three typical attack problems Examples complications at four layers, Define R = Z [ x ] = ( x 761 − x − 1); Secret key: interfaces between layers. “small” = all coeffs in {− 1 ; 0 ; 1 } ; Public key talk emphasizes top layer. w = 286; q = 4591. and appro Analysis of lattices Attacker wants to find Public key to attack cryptosystems small weight- w secret a ∈ R . Hoffstein–Pipher–Silverman): Problem 1: Public G ∈ R =q with G = − e=a “Approximate-SVP” aG + e = 0. Small secret e ∈ R . analysis Problem 2: Public G ∈ R =q and “SVP” aG + e = A . Small secret e ∈ R . analysis Problem 3: Public G 1 ; G 2 ∈ R =q . Public aG 1 + e 1 ; aG 2 + e 2 . Model of computation Small secrets e 1 ; e 2 ∈ R .
� � � 3 4 ypical lattice attack Three typical attack problems Examples of target complications at four layers, Define R = Z [ x ] = ( x 761 − x − 1); Secret key: small a s between layers. “small” = all coeffs in {− 1 ; 0 ; 1 } ; Public key reveals emphasizes top layer. w = 286; q = 4591. and approximation of lattices Attacker wants to find Public key for “NTRU” cryptosystems small weight- w secret a ∈ R . Hoffstein–Pipher–Silverman): Problem 1: Public G ∈ R =q with G = − e=a , and A ximate-SVP” aG + e = 0. Small secret e ∈ R . analysis Problem 2: Public G ∈ R =q and “SVP” aG + e = A . Small secret e ∈ R . analysis Problem 3: Public G 1 ; G 2 ∈ R =q . Public aG 1 + e 1 ; aG 2 + e 2 . computation Small secrets e 1 ; e 2 ∈ R .
3 4 attack Three typical attack problems Examples of target cryptosystems layers, Define R = Z [ x ] = ( x 761 − x − 1); Secret key: small a ; small e . layers. “small” = all coeffs in {− 1 ; 0 ; 1 } ; Public key reveals multiplier layer. w = 286; q = 4591. and approximation A = aG + lattices Attacker wants to find Public key for “NTRU” (1996 cryptosystems small weight- w secret a ∈ R . Hoffstein–Pipher–Silverman): Problem 1: Public G ∈ R =q with G = − e=a , and A = 0. ximate-SVP” aG + e = 0. Small secret e ∈ R . Problem 2: Public G ∈ R =q and aG + e = A . Small secret e ∈ R . Problem 3: Public G 1 ; G 2 ∈ R =q . Public aG 1 + e 1 ; aG 2 + e 2 . computation Small secrets e 1 ; e 2 ∈ R .
Recommend
More recommend