Example: PCA of a matrix of fatty acids in margarines 1.0 C12 0.8 - PowerPoint PPT Presentation

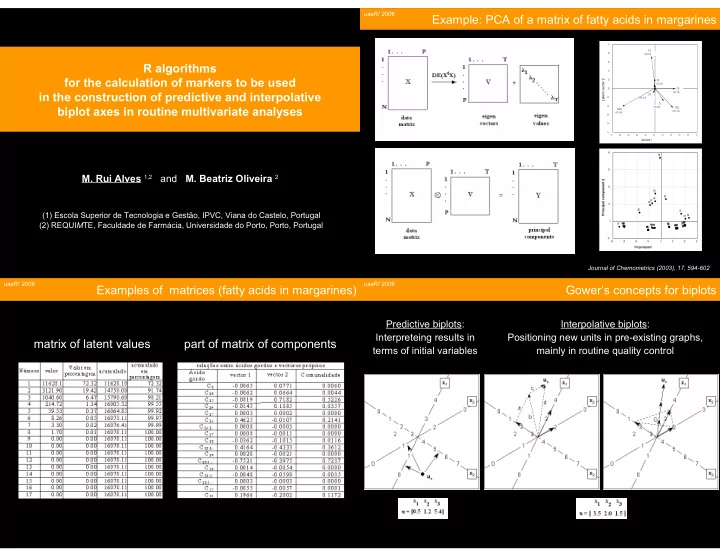
useR! 2006 Example: PCA of a matrix of fatty acids in margarines 1.0 C12 0.8 (-0.08 ; 0.72) 0.6 R algorithms 0.4 for the calculation of markers to be used 0.2 Latent vector 2 C14 (-0.01 ; 0.19) 0.0 C16 in the construction of predictive and interpolative (0.46 ; -0.01) C18 -0.2 (-0.04 ; -0.10) Ttr -0.4 biplot axes in routine multivariate analyses (0.19 ; -0.28) C18:1c C18:2cc (0.42 ; -0.43) (-0.75 ; -0.40) -0.6 -0.8 -1.0 -1.0 -0.8 -0.6 -0.4 -0.2 0.0 0.2 0.4 0.6 0.8 1.0 Latent vector 1 40 E2 30 M. Rui Alves 1,2 and M. Beatriz Oliveira 2 Principal component 2 20 B3 E3 B4 B1 B5 10 B2 (1) Escola Superior de Tecnologia e Gestão, IPVC, Viana do Castelo, Portugal A1 A4 A5 0 (2) REQUI M TE, Faculdade de Farmácia, Universidade do Porto, Porto, Portugal A2 A3 G5 G3 D2 D1 D5 G1 G4 G2 E1 E4 E5 D3 H5 F5 F3 F4 F1 C2C3 C5 C4 D4 C1 H2 H1 H3 H4 -10 -40 -30 -20 -10 0 10 20 30 Principal component 1 Journal of Chemometrics (2003), 17, 594-602 useR! 2006 useR! 2006 Examples of matrices (fatty acids in margarines) Gower’s concepts for biplots Predictive biplots: Interpolative biplots: Interpreteing results in Positioning new units in pre-existing graphs, matrix of latent values part of matrix of components terms of initial variables mainly in routine quality control

useR! 2006 useR! 2006 PCA biplots: fatty acids in margarines Problems on computation • Gower e Hand, in their book Biplots , say: Predictive biplots Interpolative biplots Interpreting results Positioning new units “(...) The main computational problems [of biplots] are in integrating different bits of available software and in finding good portable graphic facilities . • To work with bipots we used: – Genstat 5.3.1 package to develop the algorithms and carry out the analyses – Statistica for Windows to draw all the graphs based on the converted ASCII outputs produced by Genstat • We started to work with R in an attempt to provide a final, complete and more covenient solution Journal of Chemometrics (2001), 15, 71-84 Journal of Chemometrics (2003), 17, 594-602 useR! 2006 useR! 2006 Projection of markers Building biplots (PCA of fatty acids in sunflower oils) 7 7 6 6 5 5 4 4 27 27 20 16 20 16 3 44 43 3 44 43 t  V ρ t  V ρ Componente principal 2 17 Componente principal 2 17 19 19 − 1 ] [ e p ][ e p − 1  e p ] − 1 18 18 21 45 21 45 2 2 t t [  μ p − 1  − 1  − 1   V ρ 51 12 51 12 x p  s p 40 41 4041 46 46 54 47 54 47 1 25 48 1 25 48 64 26 26 62 42 10 42 10 Projection of 49 39 60 49 39 36 11 58 36 11 38 38 14 37 56 14 37 0 50 22 0 50 22 13 34 24 13 34 24 52 52 35 35 53 1 23 53 1 23 15 33 2 6 15 33 2 6 -1 9 -1 9 7 30 C 18:2cc 7 30 8 3 8 3 Markers 28 28 31 29 31 29 t V ρ ] -2 -2 [  μ p − 1  − 1 ] [ e p x p  s p 32 32 4 4 -3 -3 5 5 -4 -4 -5 -5 -6 -6 -7 -7 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 Componente principal 1 Componente principal 1 10 C 16 8 0.20 7.0 0.28 6 4 0.30 0.15 6.5 2 componente 2 0.32 64 0 62 30.5 60 C 18:1 28.5 26.5 24.5 58 56 0.10 -2 0.34 6.0 C 18:2 -4 0.36 0.05 -6 5.5 variáveis -8 muito C 16:1 longas -10 -10 -8 -6 -4 -2 0 2 4 6 8 10 5.0 C 20 componente 1

useR! 2006 useR! 2006 Strategies for the automation of the process Algorithm for the selection based on predictive powers u n  pred  = read in the graph = 0,5 Two strategies were devised: u n  inicial  = initial value = 0,4 The first, more obvious, is to create an object containing the markers, the erro  u n  = 0,5− 0,4 = 0,1 axis, the scale values and variable’s name. u n  pred  − u n  incial   x p  = 1 N • Project the object. N ∑ n = 1 erro • Live it in the graph if it fits well s p • Delete it otherwise (too long or too short vectors) • This procedure would require interactivity facilities Define a tolerance value The second, more mathematical: if error  x p  ¿ tolerance ⇒ accept x p • Find a way for the evaluation of variables’ predictive powers • Leave in the graph variables displaying high predictive power if error  x p  ¿ tolerance ⇒ reject x p • Delete them otherwise • Draw the graphs (only with automatically selected variables) useR! 2006 useR! 2006 for (i in 1:(Q-1)) { Evaluation of predictive power and decision for (j in (i+1):Q) { print("component"); print(i); print("component"); print(j) # latent variables for a pair of components only V2Dim[,1] <- RedV[,i] V2Dim[,2] <- RedV[,j] MStdE <- list() Pr ediction = X ⊗ V 2dim ⊗ V [ k , ] for (k in 1:P) { 2 dim t # evaluation of variable' s predictive power print("variavel") ; print(k) UnitsStdE = abs  X [ ,k ] − Pr ediction  VarDir <- matrix(data=(V2Dim[k,]),nrow=1,ncol=2) MeanStdE = N − 1 × 1 t ⊗ UnitSdtE Pred <- XStd %*% V2Dim %*% t(VarDir) UnitStdE <- abs(XStd[,k] - Pred) VarE <- (t(ColN1s) %*% UnitStdE)/N if  MeanStdE  Tolerance  MStdE[[k]] <- VarE print(MStdE[[k]]) t  V ρ t  V ρ project var iable − 1 − 1 ] [ e p ][ e p − 1  e p ] if (MStdE[[k]] < Tolerance) { t t [  μ p − 1  − 1  − 1   V ρ x p  s p Zeros <- matrix(0,c(P,1)) else Zeros[k,] <- 1 Adj1 <- t(Zeros) %*% V2Dim %*% t(V2Dim) %*% Zeros pr int  ital deleted  Adj2 <- (ColM1s %*% (1/Adj1) %*% t(Col2_1s)) EPred <- Adj2 * (ScMat[[k]] %*% V2Dim) print(EPred) plot(EPred[,1],EPred[,2]) } else print("deleted") } } }

useR! 2006 useR! 2006 Example of results provided by the algorithm What needs to be done and acknowledgments [1] "component" [1] 1 • Reminding Gower and Hand: “(...) The main computational [1] "component" problems [dos biplots] are in integrating different bits of available [1] 2 software and in finding good portable graphic facilities . [1] "variavel" [1] 1 [,1] • The algorithms are done, although probably not in the best or more [1,] 0.6583496 efficient way, but they provide correct results [1] "deleted" [1] "variavel" • Produce biplots by making the graphs of components and merging [1] 2 the graphs of individual variables as objects [,1] [1,] 0.5805472 [1] "deleted" • Multivariate analyses can therefore be made fully automatic, [1] "variavel" including the interpretation processes [1] 3 [,1] • Paul Murrell and Robert Gittins provided valuable information on [1,] 0.2413512 graphs and strategies to finalize the work, but unfortunately we did [,1] [,2] not find the time necessary to do it [1,] 2.6066496 4.1854190 [2,] 1.4223328 2.2837971 [3,] 0.2380160 0.3821751 [4,] -0.9463008 -1.5194468 [5,] -2.1306176 -3.4210688 useR! 2006 Thank you