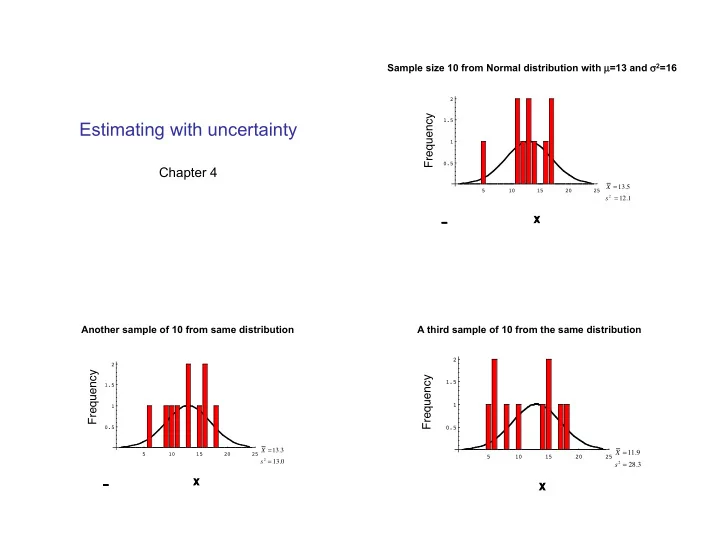

Sample size 10 from Normal distribution with µ =13 and � 2 =16 2 Frequency � 1.5 Estimating with uncertainty 1 0.5 Chapter 4 X = 13.5 5 10 15 20 25 s 2 = 12.1 _ X Another sample of 10 from same distribution A third sample of 10 from the same distribution 2 2 Frequency � Frequency � 1.5 1.5 1 1 0.5 0.5 X = 13.3 X = 11.9 5 10 15 20 25 s 2 = 13.0 5 10 15 20 25 s 2 = 28.3 _ X X
Distribution of the means of 1000 samples, A sample of 100 from the same population distribution each of sample size 10 � Sam Sampl pl e e siz ize e 100 100 12 Frequency � 10 8 6 4 2 X = 13.0 5 10 15 20 25 s 2 = 15.6 X Distribution of the means of 1000 samples, A sample of 1000 from the same population distribution Sam Sampl pl e e siz ize e 1000 1000 each of sample size 100 � 100 80 Frequency � 60 40 20 X = 12.9 5 10 15 20 25 s 2 = 16.3 X
Variation in sample means decreases with sample size � The standard error of an n = 10 � estimate is the standard deviation of its sampling distribution. The standard error predicts the sampling n = 100 � error of the estimate. 1000 samples each � N µ = 67.4 Standard error of the mean � = 3.9 � Y = � n mean = 67.4 SD = 1.7
N Estimate of the standard error µ = 67.4 of the mean � = 3.9 µ Y = µ = 67.4 SE Y = s � Y = � = 3.9 = 1.7 n 5 n mean = 67.4 The math works! � SD = 1.7 The problem is, This gives us some knowledge of the likely we rarely know � . � difference between our sample mean and the true population mean. � In most cases, we N don � t know the real µ = 67.4 Confidence interval population � = 3.9 distribution. � The 95% confidence interval provides a plausible range for a parameter. All values We only have a for the parameter lying within the interval sample. � are plausible, given the data, whereas Y = 67.1 s = 3.1 those outside are unlikely. � SE Y = s = 3.1 = 1.4 n 5 We use this as an estimate of � � Y
The 2SE rule-of-thumb The interval from - 2 to + 2 � Y SE Y Y SE Y provides a rough estimate of the 95% confidence interval for the mean. � ( Assuming normally distributed population and/or sufficiently large sample size. ) � Sample means of gene sizes � Use correct language when talking about confidence intervals Not correct: � � “There is a 95% probability that the population mean is within a particular 95% confidence interval” � Correct: � � “95% of all 95% confidence intervals calculated from samples include the population mean.” � � or: � � “We are 95% confident that the population mean lies within the 95% confidence interval.” �
US counties with high kidney cancer death Confidence interval US counties with low kidney cancer Variation in cancer rates decreases death with population size of counties Wainer (2007) The most dangerous equation. American Scientist 95: 249-256. �
Pseudoreplication Example: Pseudoreplication The error that occurs when samples are not � You are interested in average pulse rate of mountain climbers. Since they are hard to find, you decide to take independent, but they are treated as though they are. � 10 measurements from each climber. You study 6 climbers, so you have 60 measurements. � What is your sample size ( n ) ? � Avoiding pseudoreplication You are interested in average pulse rate of mountain climbers. Since they are hard to find, you decide to take 10 measurements from each climber. You study 6 climbers, so you have 60 measurements. � Take the mean blood pressure for each climber, so that you have 6 pulse rates, one for each climber ( n = 6). �
Recommend
More recommend