
M. Livan The Art of Calorimetry Lecture II Energy response and Compensation 1
The Calorimeter Response Function Response = Average signal per unit of deposited energy, ✦ e.g. # photoelectrons/GeV, picoCoulombs/MeV, etc ✦ ➞ A linear calorimeter has a constant response Electromagnetic calorimeters are in general linear • • All energy deposited through ionization/excitation of absorber • If not linear ⇒ instrumental effects (saturation, leakage,....) 2
Saturation in “digital” calorimeters Gaseous detector operated in “digital” mode ✦ Geiger counters or streamer chambers ✦ Intrinsically non linear: ✦ Each charged particle creates an insensitive region along ✦ the stuck wire preventing nearby particles to be registered Density of particles increases with increasing energy ✦ ⇒ calorimeter response decreases with increasing ✦ energy Example: ✦ Calorimeter read out using wire chambers in “limited ✦ streamer” mode Energy varied by depositing n (n = 1-10) positrons of 17.5 ✦ GeV simultaneously in the calorimeter Energy deposit profile not energy dependent ✦ Calorimeter longitudinally subdivided in 5 sections ✦ 3
Saturation in “digital” calorimeters At n=6 ✦ Non linearity: ✦ 1 - 14.5 % ✦ 2 - 14.8 % ✦ 3 - 9.3 % ✦ 4 - 2.4 % ✦ 5 - 0.5 % ✦ Non-linearity in sect. 1 more than 6 times the one in sect. 4 ✦ Energy deposit in sect. 1 less than half of the one in sect. 4 ✦ Particle density in sect. 1 larger than in sect. 4 ✦ 4
Homogeneous calorimeters I ✦ Homogeneous: absorber and active media are the same ✦ Response to muons because of similarity between the energy deposit mechanism ✦ response to muons and em showers are equal ⇒ same calibration constant ⇒ e/mip=1 ✦ ✦ Response to hadrons Due to the invisible energy π /e < 1 ✦ e/mip =1 ⇒ π /mip < 1 ✦ Response to hadron showers smaller than the electromagnetic ✦ one Electromagnetic fraction (f em ) energy dependent ✦ ⇒ response to electromagnetic component increases with ✦ energy ⇒ π /e increases with energy 5
Homogeneous calorimeters II ✦ Calorimeter response to non-em component (h) energy independent ⇒ e/h > 1 (non compensating calorimeter) e/ π not a measure of the degree of non-compensation ✦ part of a pion induced shower is of em nature ✦ f em increases with energy ⇒ e/ π ⇒ tends to 1 ✦ ✦ e/h cannot be measured directly (unless…..) π = f em · e + (1 − f em ) · h π /e = f em + (1 − f em ) · h/e e/h f em function of energy e/ π = 1 − f em [1 − e/h ] 6
Hadron Showers Energy dependence EM component 7
Hadron showers: e/h and the e/ π signal ratio e/h < f em > = 1- (E/E 0 ) (k-1) e/ π = 1 − f em [1 − e/h ] E=1GeV; k=0.82 8
Homogeneous calorimeters III Response to jets ✦ Jet = collection of particles resulting from the fragmentation of ✦ a quark, a diquark or a hard gluon From the calorimetric point of view absorption of jets proceeds ✦ in a way that is similar to absorption of single hadrons (Minor) difference: ✦ em component for single hadrons are π 0 produced in the ✦ calorimeter jets contain a number of π 0 ( γ from their decays) upon ✦ entering the calorimeter (“intrinsic em component”) <fem> for jets and single hadrons different and depending on ✦ the fragmentation process No general statement can be made about differences between ✦ response to single hadrons and jets but: response to jets smaller than to electrons or gammas ✦ response to jets is energy dependent 9 ✦
Sampling calorimeters ✦ Sampling calorimeter: only part of shower energy deposited in active medium ✦ Sampling fraction f samp energy deposited in active medium f samp = total energy deposited in calorimeter ✦ f samp is usually determined with a mip (dE/dx at minimum) ✦ N.B. mip’s do not exist ! ✦ e.g. D0 (em section): 3 mm 238 U (dE/dx = 61.5 MeV/layer) ✦ 2 x 2.3 mm LAr (dE/dx = 9.8 MeV/layer) ✦ f samp = 13.7% ✦ 10
The e/mip ratio D0: f samp = 13.7% ✦ However, for em showers, sampling fraction is only 8.2% ✦ ⇒ e/mip ≈ 0.6 ✦ e/mip is a function of shower depth, in U/LAr it decreases ✦ e/mip increases when the sampling frequency becomes very ✦ high ✦ What is going on ? Photoelectric effect: σ ∝ Z 5 , (18 / 92) 5 = 3 · 10 -4 ✦ ⇒ Soft γ s are very inefficiently sampled ✦ Effects strongest at high Z, and late in the shower development ✦ The range of the photoelectrons is typically < 1 mm ✦ Only photoelectrons produced near the boundary between ✦ active and passive material produce a signal ⇒ if absorber layers are thin, they may contribute to the signals ✦ 11
Gammas At high energy γ /mip ≈ e/mip ✦ Below 1 MeV the efficiency for γ detection drops ✦ spectacularly due to the onset of the photoelectric effect 12
The e/mip ratio: dependence on sampling frequency Only photoelectrons produced in a very thin absorber layer near ✦ the boundary between active and passive materials are sampled Increasing the sampling frequency (thinner absorber plates) ✦ increases the total boundary surface 13
Sampling calorimeters: the e/mip signal ratio e/mip larger for LAr (Z=18) than for scintillator ✦ e/mip ratio determined by the difference in Z values ✦ between active and passive media 14
Hadronic shower response and the e/h ratio The hadronic response is not constant ✦ f em, and therefore e/ π signal ratio is a function of energy ✦ ➙ If calorimeter is linear for electrons, it is non-linear for ✦ hadrons Energy-independent way to characterize hadron calorimeters: e/h ✦ e = response to the em shower component ✦ h = response to the non-em shower component ✦ → Response to showers initiated by pions: ✦ e/h R π = f em e + [1 − f em ] h e/ π = → 1 − f em [1 − e/h ] e/h is inferred from e/ π measured at several energies (f em values) ✦ Calorimeters can be ✦ Undercompensating (e/h > 1) ✦ Overcompensating (e/h < 1) ✦ Compensating (e/h =1) ✦ 15
Response function of a non compensating calorimeter 16
Signal non-linearity 17
Compensation In order to understand how compensation could be achieved, one ✦ should understand in detail the response to the various types of particles that contribute to the calorimeter signals Energy deposition mechanisms that play a role in the absorption of ✦ the non-em shower energy: Ionization by charged pions (Relativistic shower component). ✦ The fraction of energy carried by these particles is called f rel Ionization by spallation protons (non-relativistic shower ✦ component). The fraction of energy carried by these particles is called f p Kinetic energy carried by evaporation neutrons may be deposited ✦ in a variety of ways. The fraction of energy carried by these particles is called f n The energy used to release protons and neutrons from ✦ calorimeter nuclei, and the kinetic energy carried by recoil nuclei do not lead to a calorimeter signal. This energy represent the invisible fraction f inv of the non-em shower energy 18
Non-em calorimeter response ✦ h can be written as follows: h = f rel · rel + f p · p + f n · n + f inv · inv f rel + f p + f n + f inv = 1 ✦ rel, p, n and inv denote the calorimeter responses ✦ Normalizing to mips and eliminating the last term e e/mip h = f rel · rel/mip + f p · p/mip + f n · n/mip ✦ The e/h value can be determined once we know its response to the three components of the non-em shower components ✦ For compensation the response to neutron is crucial ✦ Despite the fact that n carry typically not more than ~10% of the non-em energy, their contribution to the signal can be much larger than that 19
Compensation - The role of neutrons Neutrons only loose their energy through the products of the ✦ nuclear reactions they undergo Most prominent at the low energies typical for hadronic shower ✦ neutrons is the elastic scattering. In this process the transferred energy fraction is on average: ✦ f elastic = 2A/(A+1) 2 Hydrogen f elastic = 0.5 Lead f elastic = 0.005 ✦ Pb/H 2 calorimeter structure (50/50) ✦ 1 MeV n deposits 98% in H 2 ✦ ⇒ n/mip = 45 mip deposits 2.2% in H 2 ✦ ⇒ n/mip = 350 Pb/H 2 calorimeter structure (90/10) ✦ Recoil protons can be measured! ✦ ⇒ Neutrons have an enormous potential to amplify hadronic ✦ shower signals, and thus compensate for losses in invisible energy Tune the e/h value through the sampling fraction! ✦ 20
Compensation in a Uranium/gas calorimeter 21
Compensation: the crucial role of the sampling fraction 22
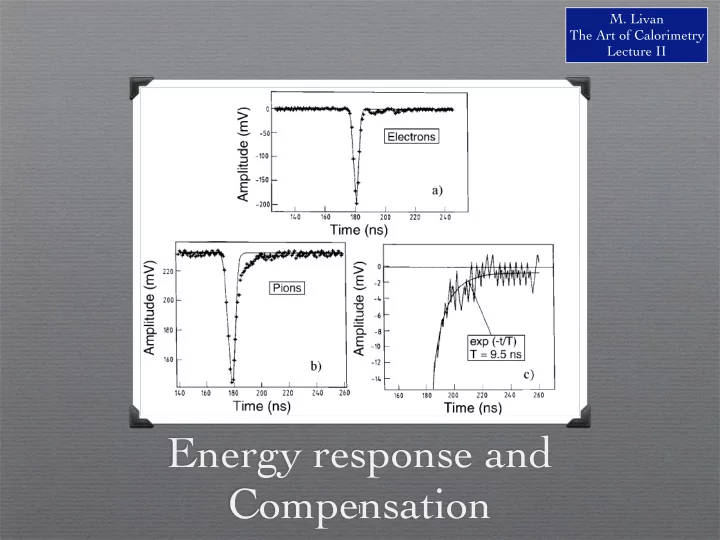
Compensation: slow neutrons and the signal’s time structure Average time ✦ between elastic n-p collisions: 17 ns in polystyrene Measured value ✦ lower (10 ns) due to elastic or inelastic neutron scattering off other nuclei present in the calorimeter structure (Pb, C and O) 23
Compensation ✦ All compensating calorimeters rely on the contribution of neutrons to the signals ✦ Ingredients for compensating calorimeters Sampling calorimeter ✦ Hydrogenous active medium (recoil p!) ✦ Precisely tuned sampling fraction ✦ e.g. 10% for U/scintillator, 3% for Pb/scintillator,……. ✦ ✦ No way to get compensation in homogeneous calorimeters ✦ No way to get compensation in sampling calorimeters with non hydrogenous active medium, e.g. LAr or Si 24
Recommend
More recommend