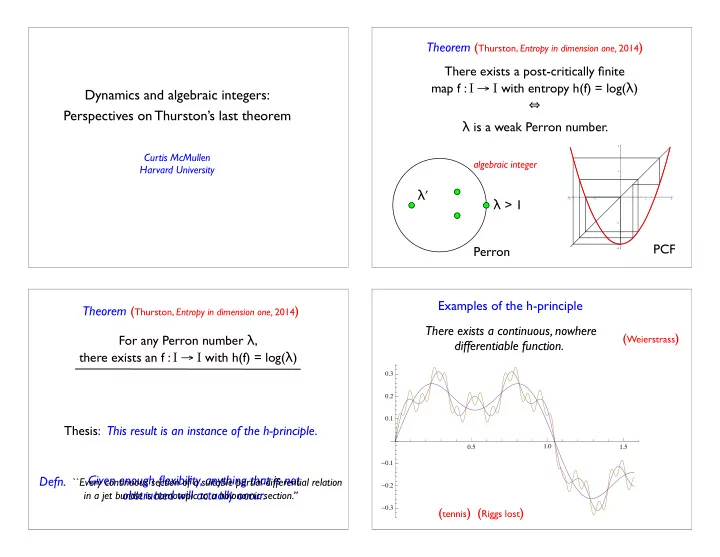

Theorem ( Thurston, Entropy in dimension one, 2014 ) There exists a post-critically finite map f : I → I with entropy h(f) = log( λ ) Dynamics and algebraic integers: ⇔ Perspectives on Thurston’s last theorem λ is a weak Perron number. 2 Curtis McMullen algebraic integer Harvard University 1 λ ’ λ > 1 -2 -1 1 2 -1 PCF Perron -2 Examples of the h-principle Theorem ( Thurston, Entropy in dimension one, 2014 ) There exists a continuous, nowhere ( Weierstrass ) For any Perron number λ , differentiable function. there exists an f : I → I with h(f) = log( λ ) 0.3 0.2 0.1 Thesis: This result is an instance of the h-principle . 1.0 0.5 1.5 - 0.1 Given enough flexibility, anything that is not Defn. ``Every continuous section of a suitable partial differential relation - 0.2 obstructed will actually occur. in a jet bundle is homotopic to a holonomic section.’’ - 0.3 ( tennis ) ( Riggs lost )
A closed hyperbolic surface embeds The sphere can be turned inside-out. ( Smale ) isometrically (C 1 ) into R 3 . ( Nash-Kuiper ) ( Thurston ) There exists a path-isometry f : S 2 ➝ R 2 . A manifold admits a codimension 1 ( Thurston ) foliation ⇔ χ (M) = 0 (Length of γ = length of f ∘ γ .) ( Gromov ) f ( Lawson, Haefliger, Bott )
Constructing P from λ deg( λ ) = d There exists a Perron-Frobenius matrix P in M n ( Z ) with spectral radius ρ (P) = λ T in M d ( Z ) ( Lind ) PR d T ⇔ Tv = λ v λ is a Perron number. Q find convex n-gon Q, T(Q) ⊂ Q [v] algebraic integer ⇒ PF matrix P in M n ( R ) , Perron-Frobenius means P ij ≥ 0 ρ ( P ) = λ . λ ’ and P kij > 0 for some k. λ > 1 Even for cubic λ , we may be forced (M, Lind) Perron to take n ≫ 0. Golden mean example Theorem ( Thurston ) There exists a post-critically finite map f : I → I with entropy h(f) = log( λ ) A B � ⇔ 0.8 B λ is a (weak) Perron number. 0.6 ! 0 1 P = 1 1 Why is entropy is Perron? Markov partitions 0.4 A 0.2 =unifies= √ λ = ρ ( P ) = 1 + 5 PCF multimodal maps 2 A B 0.2 0.4 0.6 0.8 1.0 pseudo-Anosov maps automorphisms of free groups For any pcf f, h(f) = log(Perron)
Constructing f from λ Quadratic Entropy Problem UNSTABLE Describe M 2 = { λ arising from quadratic f}. For any Perron number λ , there exists an f : I → I with h(f) = log( λ ) λ λ is in M 2 ⇔ 0 has finite orbit {Perron numbers λ } = ∪ M k under T λ (x) = λ (1 - |1-x|) M k = { λ arising from f with k laps} Q. Does there exist STABLE 0 2 an algorithm to test At any stage in the construction one can if λ is not in M 2 ? Known: Pisots ⊂ M 2 increase # laps or size of post-critical set. Unknown (e.g.): Is Lehmer’s number in M 2 ? [Proof. First step is Lind’s theorem. ] Surface Entropy Conjecture STABLE Minimum entropy problem for surfaces (open) There exists a pseudo-Anosov map log( δ g ) = min {h(f) : f pseudo-Anosov f : S → S with h(f) = log( λ ) ( Fried 1985, Thurston) on a surface of genus g} ⇔ λ is a biPerron number. = length of shortest geodesic on M g . ! 2 1 Example: δ 1 = root of t 2 -3t+1 1 1 algebraic unit δ 2 = root of t 4 -t 3 -t 2 -t+1 (Cho-Ham) (Lanneau--Thiffeault) λ -1 λ > 1 Problem: Determine δ g for all g. biPerron
Q. Where do f with h(f) = O(1/g) come from? Minimum entropy problem for surfaces A. Fibered 3-manifolds. Known: δ g = 1+ O(1/g) (Penner, 1991) M = hyperbolic 3-manifold fibering over S 1 , Question: Does lim ( δ g ) g exist? (M, 2000) b 1 (M) > 1 ⇒ M fibers in infinitely many ways Conjecture: lim ( δ g ) g = δ 1 ⇒ infinitely many f : S → S whose (E. Hironaka, 2010) Theorem: limsup ( δ g ) g ≤ δ 1 mapping torus is M. • Among these are f with h(f) = O(1/g) (M, 2000) • All such f arise from finitely many M. (Aaber-Dunfield, Kin, ...) (Farb-Leininger-Margalit, 2011) Entropy of other fibrations M 3 → S 1 A manifold M from δ 1 (E. Hironaka, 2010) Teichmüller polynomial H 1 (M) M 3 = S 3 -L -1 � ⇥ 2 1 ∈ SL 2 ( Z ) 1 -1 1 1 1 = Mod 1 ∼ = Mod 0 , 4 -1 ⇔ t 2 -3t+1 Braids on 3 strands L 2g (t) = t 2g - t g (t+1+t -1 ) + 1 M 3 = S 3 -L fibers over S 1
Teichmüller polynomial: Remaining problem: lower bounds for δ g . specializations Is there a more tractable, algebraic problem? L 4 (t) = t 4 - t 3 - t 2 - t + 1 ⇒ minimal genus 2 example [f : S → S] ⇒ genus g examples with δ (f) g ∼ δ 1 , train track map [F : τ → τ ] ⇒ L 2g (t) ⇒ in agreement with conjecture Perron-Frobenius P , δ (f) = ρ (P) . L 2g (t) = t 2g - X g (X+1+X -1 ) + 1 ≈ t 2g - 3t g + 1 Symplectic structure on P ML ⇒ P is reciprocal. (eigenvalues invariant under t → 1/t) Conclusion: limsup ( δ g ) g ≤ δ 1 Q. Can we give a lower bound on ρ (P)? Minimum entropy problem for graphs Scheme of the proof P in M n ( Z ), Perron-Frobenius Theorem (M, 2013) ↺ ↺ ⇒ metrized directed graph ( Γ ,1) Min ρ (P) : P in M 2g ( Z ) is reciprocal and Perron-Frobenius #(closed loops ≤ T) ≍ ρ (P) T = Optimal metric on Γ ⇒ invariant λ ( Γ ) T Largest root of ρ (P) n ≥ λ ( Γ ) L 2g (t) = t 2g - t g (t+1+t -1 ) + 1 • Fact: { Γ : λ ( Γ ) < M} is finite Corollary Case at hand, take M=8. ρ (P) g ≥ δ 1 for all P and g. ( δ 1 ) 2 = (golden ratio) 4 =6.854...
1556 different Γ with λ ( Γ ) ≤ 6 Scheme of the proof Analyze each Γ : λ ( Γ ) < 8. (2009) List of G with λ (G) < 8 Scheme of the proof (2013) G λ (G) Γ ⇒ curve complex G ... nA 1 2 ≤ n ≤ 7 V(G) = {simple loops C in Γ } A 2 * 4 E(G) = {disjoint (C,D)} 5.82... = 3+2 √ 2 A 2 ** A 2 *** 7.46... = 4+2 √ 3 • G carries key info of Γ A 3 * 5.82... = 3+2 √ 2 • New invariant: λ ( Γ ) ≥ λ (G) Y* 7.46... = 4+2 √ 3 • {G : λ (G) < 8} = 11 G 2 A 1 3 A 1 4 A 1 5 A 1 6 A 1 7 A 1 A ∗ A ∗∗ A ∗∗∗ A ∗ Y ∗ 2 2 2 3 (RAAGs, Cartier-Foata 1968) # Γ 1 2 14 119 1556 26286 1 5 42 5 42 (Birman, 2011) Table 2. Number of trivalent Γ with a given curve complex G .
These Γ all have G = 4A 1 = Example: Concluding Remarks M : Teichmüller polynomial Γ : Perron polynomial G : Clique polynomial thermodynamic formalism convexity of pressure Problem: Determine δ g for all g? ⇒ rest of proof is SEMISTABLE now tractable. EPILOGUE SPOKEN BY PROSPERO Now my charms are all o'erthrown, * * * Gentle breath of yours my sails Must fill, or else my project fails, Which was to please. B etter for more people to be involved... it’s a fun and interesting topic.
Recommend
More recommend