Decision Tree Decision Trees A decision tree is a decision support - PDF document

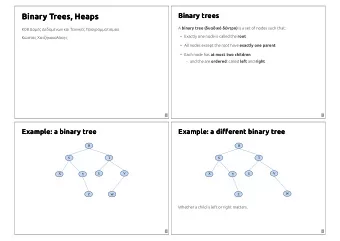
Decision Tree Decision Trees • A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible MSE 2400 EaLiCaRA consequences, including chance event Dr. Tom Way outcomes, resource costs, and utility. • It is one way to display an algorithm . MSE 2400 Evolution & Learning 2 What is a Decision Tree? Predicting Commute Time • An inductive learning task – Use particular facts to make more generalized If we leave at 10 Leave At conclusions AM and there 10 AM 9 AM are no cars 8 AM • A predictive model based on a branching series stalled on the Stall? Accident? of Boolean tests road, what will – These smaller Boolean tests are less complex than a our commute Long one-stage classifier No Yes No Yes time be? Short Long Medium Long • Let’s look at a sample decision tree… MSE 2400 Evolution & Learning 3 MSE 2400 Evolution & Learning 4 Inductive Learning Decision Trees as Rules • In this decision tree, we made a series of • We did not have to represent this tree Boolean decisions and followed the graphically corresponding branch – Did we leave at 10 AM? – Did a car stall on the road? • We could have represented as a set of – Is there an accident on the road? rules. However, this may be much harder to read… • By answering each of these yes/no questions, we then came to a conclusion on how long our commute might take MSE 2400 Evolution & Learning 5 MSE 2400 Evolution & Learning 6 1

Decision Tree as a Rule Set How to Create a Decision Tree • First, make a list of attributes that we can if hour equals 8am: Notice that all attributes measure don’t have to be used commute time is long on each path of the else if hour equals 9am: – These attributes (for now) must be discrete if accident equals yes: decision. • We then choose a target attribute that we commute time is long else : want to predict Some attributes may not commute time is medium even appear in a tree. • Then create an experience table that lists else if hour equals 10am: if stall equals yes: what we have seen in the past commute time is long else : commute time is short MSE 2400 Evolution & Learning 7 MSE 2400 Evolution & Learning 8 Sample Experience Table Choosing Attributes • The previous experience decision table Example Attributes Target Hour Weather Accident Stall Commute showed 4 attributes: hour, weather, D1 8 AM Sunny No No Long D2 8 AM Cloudy No Yes Long accident and stall D3 10 AM Sunny No No Short D4 9 AM Rainy Yes No Long • But the decision tree only showed 3 D5 9 AM Sunny Yes Yes Long D6 10 AM Sunny No No Short attributes: hour, accident and stall D7 10 AM Cloudy No No Short D8 9 AM Rainy No No Medium • Why is that? D9 9 AM Sunny Yes No Long D10 10 AM Cloudy Yes Yes Long D11 10 AM Rainy No No Short D12 8 AM Cloudy Yes No Long D13 9 AM Sunny No No Medium MSE 2400 Evolution & Learning 9 MSE 2400 Evolution & Learning 10 Occam’s Razor Choosing Attributes (1) • Methods for selecting attributes (which will • 1852 be described later) show that weather is • A “razor” is a maxim or rule of thumb not a discriminating attribute • “Entities should not be multiplied • We use the principle of Occam’s Razor : unnecessarily.” Given a number of competing hypotheses, the simplest one is preferable entia non sunt multiplicanda praeter necessitatem MSE 2400 Evolution & Learning 11 MSE 2400 Evolution & Learning 12 2

Choosing Attributes (2) Decision Tree Algorithms • The basic structure of creating a decision • The basic idea behind any decision tree algorithm is as follows: tree is the same for most decision tree – Choose the best attribute(s) to split the remaining algorithms instances and make that attribute a decision node • The difference lies in how we select the – Repeat this process for recursively for each child attributes for the tree – Stop when: • All the instances have the same target attribute value • We will focus on the ID3 algorithm • There are no more attributes developed by Ross Quinlan in 1975 • There are no more instances MSE 2400 Evolution & Learning 13 MSE 2400 Evolution & Learning 14 Identifying the Best Attributes ID3 Heuristic Refer back to our original decision tree • To determine the best attribute, we look at the ID3 heuristic Leave At • ID3 splits attributes based on their 9 AM 10 AM 8 AM entropy . Accident? Stall? • Entropy is a measure of disinformation… Long No No Yes Yes Short Long Medium Long How did we know to split on leave at then stall and accident and not weather ? MSE 2400 Evolution & Learning 15 MSE 2400 Evolution & Learning 16 This isn’t Entropy from Physics Entropy in the real world (1) • In Physics… • Entropy has to do with how rare or common an instance of information is • Entropy describes the concept that all • It's natural for us to want to use fewer bits (send things tend to move from an ordered state fewer messages) when reporting about common to a disordered state vs. rare events. • Hot is more organized than cold – How often do we hear about a safe plane landing making the evening news? • Tidy is more organized than neat – How about a crash? • Life is more organized than death – Why? The crash is rarer! • Society is more organized than anarchy MSE 2400 Evolution & Learning 17 MSE 2400 Evolution & Learning 18 3

Entropy in the real world (2) Entropy in the real world (3) • Morse code – designed using entropy • Morse code decision tree MSE 2400 Evolution & Learning 19 MSE 2400 Evolution & Learning 20 How Entropy Works Calculating Entropy • Entropy is minimized when all values of the • Calculation of entropy target attribute are the same. – Entropy(S) = ∑ (i=1 to l) -|S i |/|S| * log 2 (|S i |/|S|) – If we know that commute time will always be short , • S = set of examples then entropy = 0 • S i = subset of S with value v i under the target attribute • Entropy is maximized when there is an equal • l = size of the range of the target attribute chance of all values for the target attribute (i.e. the result is random) – If commute time = short in 3 instances, medium in 3 instances and long in 3 instances, entropy is maximized MSE 2400 Evolution & Learning 21 MSE 2400 Evolution & Learning 22 ID3 ID3 • Given our commute time sample set, we • ID3 splits on attributes with the lowest entropy can calculate the entropy of each attribute • We calculate the entropy for all values of an at the root node attribute as the weighted sum of subset entropies as follows: Attribute Expected Entropy Information Gain – ∑ (i = 1 to k) |S i |/|S| Entropy(S i ), where k is the range of Hour 0.6511 0.768449 the attribute we are testing Weather 1.28884 0.130719 • We can also measure information gain (which is Accident 0.92307 0.496479 inversely proportional to entropy) as follows: Stall 1.17071 0.248842 – Entropy(S) - ∑ (i = 1 to k) |S i |/|S| Entropy(S i ) MSE 2400 Evolution & Learning 23 MSE 2400 Evolution & Learning 24 4

Problems with ID3 Problems with Decision Trees • While decision trees classify quickly, the • ID3 is not optimal time for building a tree may be higher than – Uses expected entropy reduction, not actual another type of classifier reduction • Must use discrete (or discretized) • Decision trees suffer from a problem of attributes errors propagating throughout a tree – What if we left for work at 9:30 AM? – A very serious problem as the number of – We could break down the attributes into classes increases smaller values… MSE 2400 Evolution & Learning 25 MSE 2400 Evolution & Learning 26 Error Propagation Error Propagation Example • Since decision trees work by a series of local decisions, what happens when one of these local decisions is wrong? – Every decision from that point on may be wrong – We may never return to the correct path of the tree MSE 2400 Evolution & Learning 27 MSE 2400 Evolution & Learning 28 Problems with ID3 Problems with ID3 • We can use a technique known as discretization • If we broke down leave time to the • We choose cut points , such as 9AM for splitting minute, we might get something like continuous attributes this: • These cut points generally lie in a subset of boundary points , such that a boundary point is 8:02 AM 8:03 AM 9:05 AM 9:07 AM 9:09 AM 10:02 AM where two adjacent instances in a sorted list have different target value attributes Long Medium Short Long Long Short Since entropy is very low for each branch, we have n branches with n leaves. This would not be helpful for predictive modeling. MSE 2400 Evolution & Learning 29 MSE 2400 Evolution & Learning 30 5