( ( ) ) ( ) ( ) = = Work = h log t n B- B -Trees - PDF document

Nov 05, 2023 •240 likes •287 views

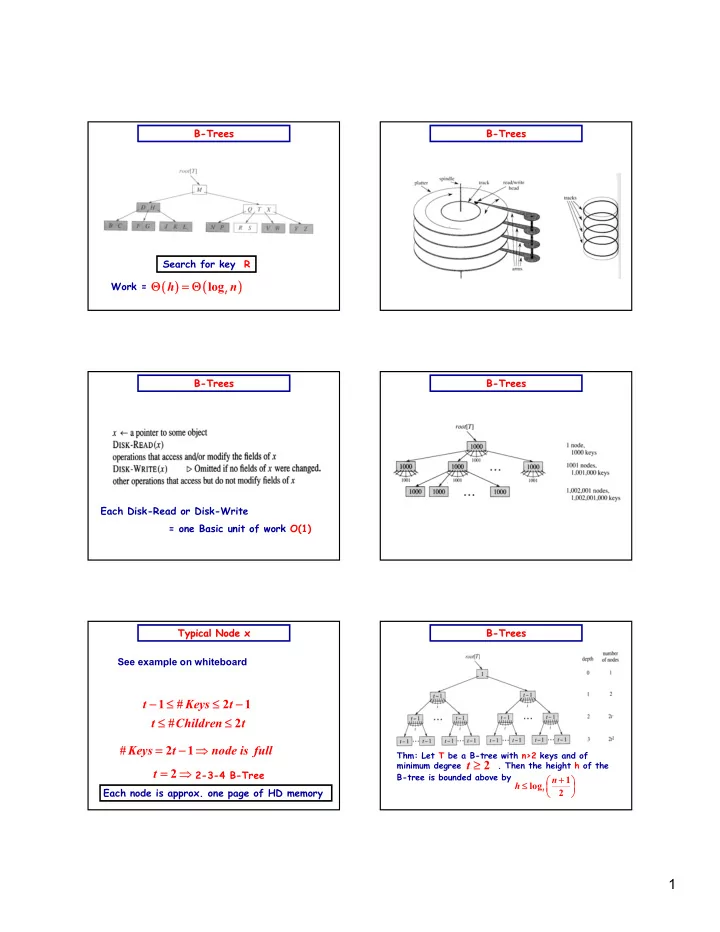
B- B -Trees Trees B B- -Trees Trees Search for key R ( ( ) ) ( ) ( ) = = Work = h log t n B- B -Trees Trees B B- -Trees Trees Each Disk-Read or Disk-Write = one Basic unit of work O(1) Typical Node x

B- B -Trees Trees B B- -Trees Trees Search for key R ( ( ) ) ( ) ( ) Θ Θ = = Θ Work = h log t n B- B -Trees Trees B B- -Trees Trees Each Disk-Read or Disk-Write = one Basic unit of work O(1) Typical Node x Typical Node x B B- -Trees Trees See example on whiteboard − − ≤ ≤ ≤ − t 1 # Keys 2 t 1 ≤ ≤ ≤ ≤ t # Children 2 t = = − − ⇒ # Keys 2 t 1 node is full Thm: Let T be a B-tree with n>2 keys and of t ≥ minimum degree . Then the height h of the 2 t = ⇒ 2-3-4 B-Tree 2 B-tree is bounded above by +   n 1 ≤   h log Each node is approx. one page of HD memory t   2 1
B- B -Trees Trees B B- -Trees Trees Search for key R ( ) ( ) ( ( ) ) ( ( ) ) Θ Θ = Θ = ( ) ( ) Θ Θ = = Θ Work = h log t n h log t n B- B -Trees Trees B B- -Tree Insertion Tree Insertion To INSERT, we will need procedures for splitting full nodes B- B -Trees Trees B- B -Trees Trees B-Tree-Split 2
B- B -Trees Trees B B- -Trees Trees B-Tree-Split B- B -Trees Trees B B- -Trees Trees Splitting a root node Inserting Keys in a B Inserting Keys in a B- -Tree Tree B B- -Tree Deletion Tree Deletion We must make sure that the number of keys in a non-root node is always at least t 3
Deleting Keys in a B Deleting Keys in a B- -Tree Tree Deleting Keys in a B Deleting Keys in a B- -Tree (Cont.) Tree (Cont.) 4

Recommend

/ + - * * 5 3 2 6 5 2 Examples Binary Trees BSTs Augmenting BinExpr General Trees

Trees Readings: HtDP , sections 14, 15, 16. Topics: Introductory examples and terminology Binary trees Binary search trees Augmenting trees Binary expression trees General arithmetic expression trees Nested lists Examples Binary Trees

1.19k views • 31 slides

Trees Eric McCreath Overview In this lecture we will explore: general trees, binary trees,

Trees Eric McCreath Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 2 Trees Trees are recursive data structures. They are useful for: representing items that have a tree

622 views • 27 slides

2-3-4 Trees and Red- Black Trees 204 erm CS 16: Balanced Trees 2-3-4 Trees Revealed Nodes

CS 16: Balanced Trees 2-3-4 Trees and Red- Black Trees 204 erm CS 16: Balanced Trees 2-3-4 Trees Revealed Nodes store 1, 2, or 3 keys and have 2, 3, or 4 children, respectively All leaves have the same depth k n r b e h n r b e

800 views • 31 slides

Algorithms and Data Structures Balanced Trees (AVL-Trees, (a,b)-Trees, Red-Black-Trees)

Algorithms and Data Structures Balanced Trees (AVL-Trees, (a,b)-Trees, Red-Black-Trees) Albert-Ludwigs-Universitt Freiburg Prof. Dr. Rolf Backofen Bioinformatics Group / Department of Computer Science Algorithms and Data Structures, January

884 views • 55 slides

AVL TREES Height Balance : AVL Trees h 1 h 2 | h - h | 1 AVL AVL 2 1 non-AVL trees

AVL TREES Height Balance : AVL Trees h 1 h 2 | h - h | 1 AVL AVL 2 1 non-AVL trees AVL trees S. Prasitjutrakul 1994 AVL Trees : I nsertion m m k k k u u k k m m v t u m m t t u k m u k u p v t k p v v

320 views • 16 slides

The number of spanning trees of random 2 -trees Stephan Wagner (joint work with Elmar Teufl)

The number of spanning trees of random 2 -trees Stephan Wagner (joint work with Elmar Teufl) Stellenbosch University AofA15 Strobl, 8 June, 2015 2 -trees 2 -trees are constructed recursively: Spanning trees of 2 -trees S. Wagner,

822 views • 61 slides

Trees I think that I shall never see Trees I A poem lovely as a tree -- J. Kilmer Trees

Trees I think that I shall never see Trees I A poem lovely as a tree -- J. Kilmer Trees Anatomy of a Tree a In CS, we look at trees Node from the bottom up Basic element of the tree b c Contains a piece of

321 views • 5 slides

Trees Russell Impagliazzo and Miles Jones Thanks to Janine Tiefenbruck

Trees Russell Impagliazzo and Miles Jones Thanks to Janine Tiefenbruck http://cseweb.ucsd.edu/classes/sp16/cse21-bd/ April 29, 2016 Another Special Type of Graph: Trees Trees 1. Definitions of trees 2. Properties of trees 3. Revisiting uses of

837 views • 37 slides

Trees a tree represents a hierarchy - organization structure of a corporation Electronics

T REES trees binary trees traversals of trees template method pattern data structures for trees Trees 1 Trees a tree represents a hierarchy - organization structure of a corporation Electronics RUs R&D

434 views • 18 slides

Trees Applied Multivariate Statistics Spring 2012 Overview Intuition for Trees

Trees Applied Multivariate Statistics Spring 2012 Overview Intuition for Trees Regression Trees Classification Trees 1 Idea of Trees: Regression Trees Continuous response Binary Tree y Y=1.2 X 1 X>1 Y=1.4 Y=0.7 2 X

767 views • 17 slides

Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition

1 CSCI 104 B-Trees (2-3, 2-3-4) and Red/Black Trees Mark Redekopp David Kempe 2 An example of B-Trees 2-3 TREES 3 Definition 2-3 Tree is a tree where a 2 Node 4 Non-leaf nodes have 1 value & 2 children or 2 values and 3

998 views • 75 slides

Splay Trees and B-Trees CSE 373 Data Structures Lecture 9 Readings Reading Sections

Splay Trees and B-Trees CSE 373 Data Structures Lecture 9 Readings Reading Sections 4.5-4.7 4/14/03 Splay Trees and B-Trees - 2 Lecture 9 Self adjusting Trees Ordinary binary search trees have no balance conditions what

371 views • 33 slides

A Datatype for Binary Trees Functions on Trees Amtoft from Hatcliff Binary Trees One of many

A Datatype for Binary Trees Functions on Trees Amtoft from Hatcliff Binary Trees One of many possible definitions (no interior values) Examples General Trees datatype b i t r e e = Leaf i n t of | Node of b i t r e e b i t r e e

536 views • 8 slides

Visualizing Networks and Trees Arrange Networks and Trees

Visualizing Networks and Trees Arrange Networks and Trees Node-Link Diagrams for Trees The most common visual representa>on Nodes: point marks;

519 views • 15 slides

Trees Chapter 11 Chapter Summary Introduction to Trees Applications of Trees Tree

Trees Chapter 11 Chapter Summary Introduction to Trees Applications of Trees Tree Traversal Spanning Trees Minimum Spanning Trees Introduction to Trees Section 11.1 Section Summary Introduction to Trees Rooted Trees

639 views • 42 slides

Trees & Binary Search Trees Department of Computer Science University of Maryland, College

CMSC 132: Object-Oriented Programming II Trees & Binary Search Trees Department of Computer Science University of Maryland, College Park Trees Trees are hierarchical data structures One-to-many relationship between elements

737 views • 29 slides

CS 220: Discrete Structures and their Applications Trees Chapter 11 in zybooks trees A tree is

CS 220: Discrete Structures and their Applications Trees Chapter 11 in zybooks trees A tree is an undirected graph that is connected and has no cycles. rooted trees Rooted trees. Given a tree T, choose a root node r and orient each edge

814 views • 52 slides

AVL Trees AVL Trees K08

AVL Trees AVL Trees K08 / 1 Balanced trees Balanced trees O ( h ) We saw that most of the algorithms in BSTs

1.2k views • 50 slides

General Trees children that any node may have. Chapter 7 Well, non-binary trees anyway.

General Trees General trees are similar to binary trees, except that there is no restriction on the number of General Trees children that any node may have. Chapter 7 Well, non-binary trees anyway. General Trees More formally A

283 views • 6 slides

Balanced Search Trees 2-3-4 trees red-black trees References: Algorithms in Java (handout)

Balanced Search Trees 2-3-4 trees red-black trees References: Algorithms in Java (handout) Balanced search trees Dynamic sets Search Insert Delete Maximum Minimum Successor(x) (find minimum element x)

1.01k views • 68 slides

Binary trees Binary trees David Morgan Binary trees Binary trees elements have up to 2

Binary trees Binary trees David Morgan Binary trees Binary trees elements have up to 2 child elements left child sorts less, right more, than parent tree has a depth tree has a balance, comparing depths of its left and right

305 views • 5 slides

Mat 3770 Trees Grid Steiner Trees Kruskal Na ve B&B Theorems Pretaxial B&B

Mat 3770 Steiner Trees Overview Spanning Mat 3770 Trees Grid Steiner Trees Kruskal Na ve B&B Theorems Pretaxial B&B Epitaxial B&B Spring 2014 MDFDA Annealing Evolution Results Topics Mat 3770 Steiner Trees

651 views • 48 slides

kd-Trees CMSC 420 kd-Trees Invented in 1970s by Jon Bentley Name originally meant

kd-Trees CMSC 420 kd-Trees Invented in 1970s by Jon Bentley Name originally meant 3d-trees, 4d-trees, etc where k was the # of dimensions Now, people say kd-tree of dimension d Idea: Each level of the tree compares

703 views • 19 slides

Trees, Binary Search Trees, Lab 7, Project 2 Bryce Boe

Trees, Binary Search Trees, Lab 7, Project 2 Bryce Boe 2013/11/13 CS24, Fall 2013 Outline Stack/Queue Review Trees Binary Search Trees

557 views • 31 slides