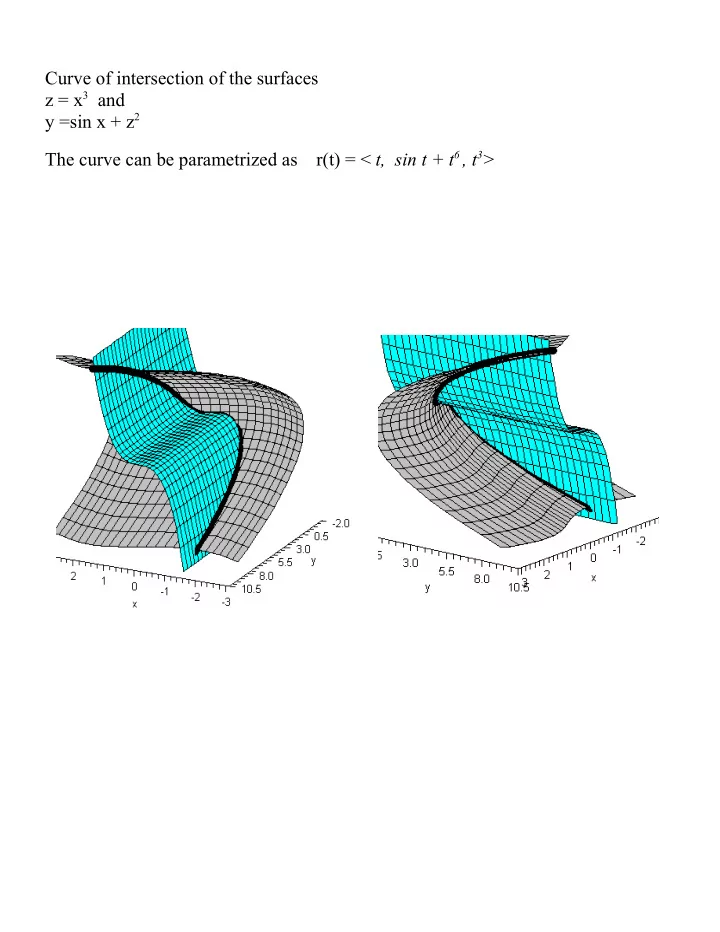
Curve of intersection of the surfaces z = x 3 and y =sin x + z 2 The - PDF document

Curve of intersection of the surfaces z = x 3 and y =sin x + z 2 The curve can be parametrized as r(t) = < t, sin t + t 6 , t 3 >

Curve of intersection of the surfaces z = 3 x 2 + y 2 (elliptic paraboloid) and y = x 2 (parabolic cylinder) The curve can be parametrized as r(t) = < t, t 2 , 3t 2 + t 4 >

Curve of intersection of the surfaces x 2 + y 2 = 9 (cylinder) and z = xy (hyperbolic paraboloid) The curve can be parametrized as r(t) = < 3 cos t , 3 sin t , 9 cos t sin t >

Curve of intersection of the surfaces x 2 + z 2 = 9 (cylinder) and y = x 2 + z The curve can be parametrized as r(t) = < 3 cost , 9 cos 2 t + 3 sin t , 3 sin t >

Curve of intersection of the surfaces 2 (cone) and z =  x 2  y z = 1 + y (plane) The curve can be parametrized as r(t) = < t , (t 2 -1)/2 , 1 + (t 2 -1)/2 >

Curve of intersection of the surfaces z = x 2 + y 2 (paraboloid) and 5x – 6y + z – 8 = 0 (plane) 2 The projection of the curve on the xy plane is the circle  x  5  y − 3  2 = 93 2  4 The curve can be parametrized as 2 2 2   93 2 cos t , 3   93 2   93  3   93 r ( t ) = < − 5 2 sin t , − 5 > 2 cos t  2 sin t 