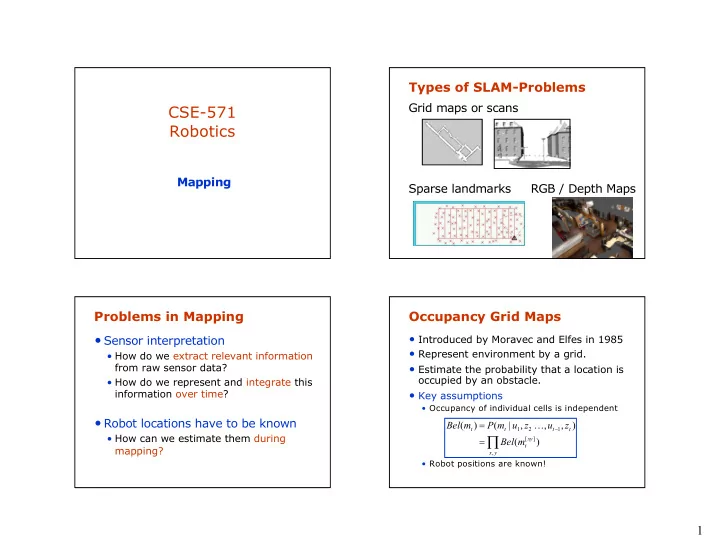

Types of SLAM-Problems Grid maps or scans CSE-571 Robotics Mapping Sparse landmarks RGB / Depth Maps Problems in Mapping Occupancy Grid Maps • Sensor interpretation • Introduced by Moravec and Elfes in 1985 • Represent environment by a grid. • How do we extract relevant information from raw sensor data? • Estimate the probability that a location is occupied by an obstacle. • How do we represent and integrate this information over time? • Key assumptions • Occupancy of individual cells is independent • Robot locations have to be known = Bel ( m ) P ( m | u , z ! , u , z ) - t t 1 2 t 1 t • How can we estimate them during Õ = [ xy ] Bel ( m ) t mapping? x , y • Robot positions are known! 1
Inverse Sensor Model Updating Occupancy Grid Maps for Occupancy Grid Maps • Idea: Update each individual cell Combination of linear function and Gaussian: using a binary Bayes filter. ∑ [ xy ] | m t − 1 [ xy ] ) = η p ( z t | m t [ xy ] ) [ xy ] , u t − 1 ) Bel ( m t − 1 [ xy ] ) Bel ( m t p ( m t [ xy ] m t − 1 • Additional assumption: Map is static. [ xy ] ) = η p ( z t | m t [ xy ] ) Bel ( m t − 1 [ xy ] ) Bel ( m t ( ) ( ) ( ) ( ) = - + B m [ xy ] log odds m [ xy ] | z , x log odds m [ xy ] B m [ xy ] t t t t t t - 1 Incremental Updating Alternative: Simple Counting of Occupancy Grids (Example) • For every cell count • hits( x , y ): number of cases where a beam ended at < x , y> • misses( x , y ): number of cases where a beam passed through <x,y> hits( x , y ) = Bel ( m [ xy ] ) + hits( x , y ) misses( x , y ) • Assumption: P ( occupied ( x,y )) = P ( reflects ( x,y )) 2
Resulting Map Obtained with Occupancy Grids: From scans to maps Ultrasound Sensors Tech Museum, San Jose OctoMap A Probabilistic, Flexible, and Compact 3D Map Representation for Robotic Systems K.M. Wurm, A. Hornung , M. Bennewitz, C. Stachniss, W. Burgard University of Freiburg, Germany CAD map occupancy grid map http://octomap.sf.net 3
Robots in 3D Environments 3D Map Requirements § Full 3D Model § Volumetric representation § Free-space § Unknown areas (e.g. for exploration) § Updatable § Probabilistic model (sensor noise, changes in the environment) Mobile manipulation Outdoor navigation § Update of previously recorded maps § Flexible § Map is dynamically expanded § Multi-resolution map queries § Compact § Memory efficient § Map files for storage and exchange Humanoid robots Flying robots Map Representations Map Representations Pointclouds 3D voxel grids § Pro: § Pro: § No discretization of data § Probabilistic update § Mapped area not limited § Constant access time § Contra: § Contra: § Unbounded memory usage § Memory requirement § No direct representation of free or § Extent of map has to be known unknown space § Complete map is allocated in memory 4
Map Representations Map Representations 2.5D Maps Octrees § 2D grid § Height value(s) in each cell § Tree-based data structure § Recursive subdivision of § Pro: space into octants § Memory efficient § Volumes allocated § Contra: as needed § Not completely probabilistic § No distinction between free and unknown § Multi-resolution space Map Representations OctoMap Framework Octrees § Based on octrees § Probabilistic representation of occupancy § Pro: including unknown § Full 3D model § Supports multi-resolution map queries § Probabilistic § Lossless compression § Flexible, multi-resolution § Compact map files § Memory efficient § Contra: § Open source implementation as C++ § Implementation can be tricky library available at http://octomap.sf.net (memory, update, map files, …) 5
Probabilistic Map Update Probabilistic Map Update § Occupancy modeled as recursive § Clamping policy ensures updatability [Yguel ‘ 07] binary Bayes filter [Moravec ‘ 85] § Update of inner nodes enables multi- resolution queries § Efficient update using log-odds notation 0.08 m 0.64 m 1.28 m Lossless Map Compression Map Files § Lossless pruning of nodes with identical § Maximum-likelihood map stored as children compact bitstream § Occupied, free, and unknown areas § High compression ratios esp. in free space § Very moderate space requirements (usually less than 2 MB) [Kraetzschmar 04] 6
Examples Examples: Office Building § Cluttered office environment § Freiburg, building 079 Map resolution: 2 cm Examples: Large Outdoor Areas Examples: Tabletop § Freiburg computer science campus (292 x 167 x 28 m ³ , 20 cm resolution) 7
Adding Color Memory Usage FR-079 dataset Freiburg campus outdoor dataset Memory Usage Insert time for 100,000 beams 8
OctoMap Implementation § Open source C++ library § Fully documented § Can be easily adapted to your projects § ROS integration § Includes OpenGL viewer § Already used by several other researchers http://octomap.sf.net 9
Recommend
More recommend