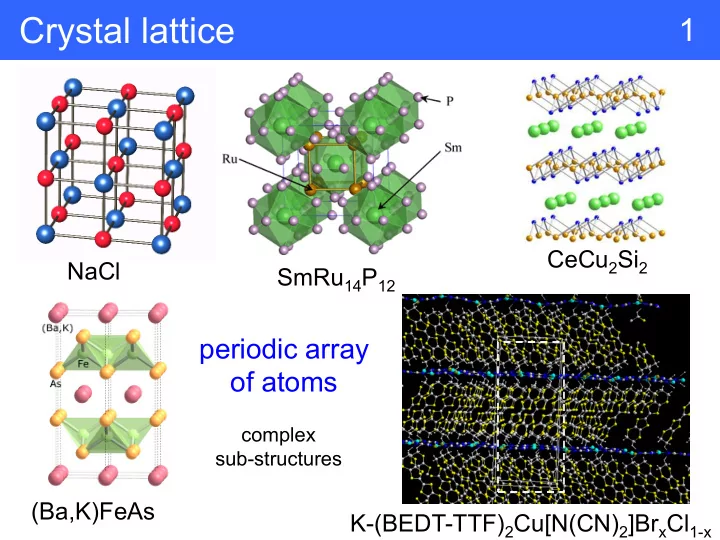
Crystal lattice 1 CeCu 2 Si 2 NaCl SmRu 14 P 12 periodic array of - PowerPoint PPT Presentation

Crystal lattice 1 CeCu 2 Si 2 NaCl SmRu 14 P 12 periodic array of atoms complex sub-structures (Ba,K)FeAs K-(BEDT-TTF) 2 Cu[N(CN) 2 ]Br x Cl 1-x

Crystal lattice 2 unit cell Wigner-Seitz cell lattice vectors primitive lattice vectors basis set

Crystal lattice - Space Group 3 general symmetry operations in a crystal lattice r 0 = g ~ a = { g | ~ a } ~ ~ r + ~ { g | ~ a } space group element r basic elements g ~ r { E | ~ a } basic translations ~ { g | ~ r 0 ~ 0 } rotations, reflections, inversions a { g 0 | ~ a 0 } screw axis, glide plane ~ r screw axis point group element g ∈ P g 0 60 o rotation a 0 ~ + around z-axis ~ lattice vector a not a not a basic lattice point group vector element

Crystal lattice - Space Group 4 R space group is a group a 0 + ~ a }{ g 0 | ~ a 0 } = { gg 0 | g ~ { g | ~ a } multiplication associative { E | ~ { E | ~ a + ~ 0 } unit element 0 }{ g | ~ a } = { Eg | E ~ 0 } = { g | ~ a } a } − 1 = { g − 1 | − g − 1 ~ inverse { g | ~ a } a } = { E | ~ a } − 1 { g | ~ a } = { g − 1 | − g − 1 ~ a } = { g − 1 g | g − 1 ~ a − g − 1 ~ { g | ~ a }{ g | ~ 0 } 230 space groups = symmorphic 73 symmorphic + 157 non-symmorphic space groups with screw axes and glide planes non-symmorphic non-symmorphic