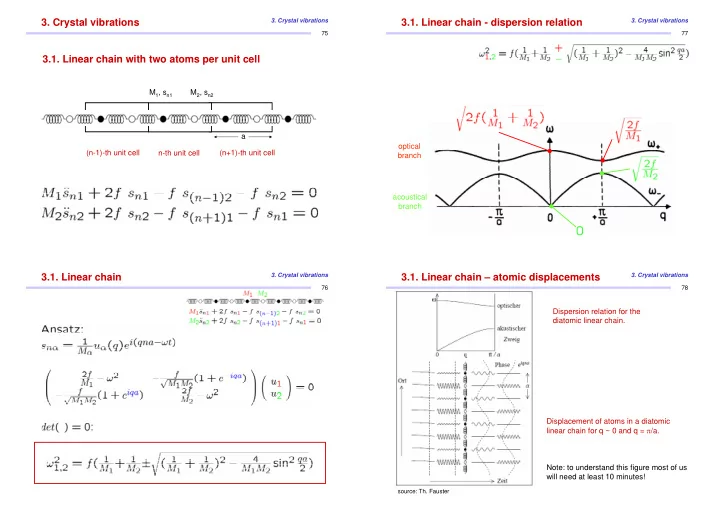
3. Crystal vibrations 3. Crystal vibrations 3.1. Linear chain - - PowerPoint PPT Presentation

3. Crystal vibrations 3. Crystal vibrations 3.1. Linear chain - dispersion relation 3. Crystal vibrations 75 77 3.1. Linear chain with two atoms per unit cell M 1 , s n1 M 2 , s n2 a optical (n-1)-th unit cell (n+1)-th unit cell n-th unit cell branch acoustical branch 3.1. Linear chain 3. Crystal vibrations 3.1. Linear chain – atomic displacements 3. Crystal vibrations 76 78 Dispersion relation for the diatomic linear chain. Displacement of atoms in a diatomic linear chain for q ~ 0 and q = π /a. Note: to understand this figure most of us will need at least 10 minutes! source: Th. Fauster

3.2. Lattice vibrations (3 dim.) 3. Crystal vibrations 3.2. Lattice vibrations (3 dim.) 3. Crystal vibrations 79 81 Example: ( Si, Ge, diamond) fcc lattice with basis of 2 atoms (a = 2) lattice planes 6 branches: 1x LA + 2x TA 1x LO + 2x TO q Longitudinal mode Transversal mode L Data points stem from inelastic neutron diffraction 3.2. Lattice vibrations (3 dim.) 3. Crystal vibrations 3.3. Thermal properties 3. Crystal vibrations 80 82 Bose Verteilung

3.3. Debye approximation 3. Crystal vibrations 3.3. Debye specific heat 3. Crystal vibrations 83 85 T 3 – law at low temperatures Specific heat of solid argon Θ D = 92 K Debye wave-vector Debye temperature (material property) 0 K 2 K 3.3. Debye specific heat 3. Crystal vibrations 3.4. Density of states 3. Crystal vibrations 86 84 Example: Si regions with low dispersion ω (q) ↔ high density of states Good approximation for small and large T

3.4. Debye approximation 3. Crystal vibrations 3.4. Debye approximation 3. Crystal vibrations 87 87 3.4. Density of states 3. Crystal vibrations 3.5. Anharmonic Effects 3. Crystal vibrations 86 88 Thermal Expansion Solid Argon a (Å) Silicon Example: Si T (K) γ negative regions with low dispersion ω (q) ↔ high density of states

3.5. Anharmonic Effects 3. Crystal vibrations 89 No umklapp: Heat conduction by phonons NaF Umklapp: