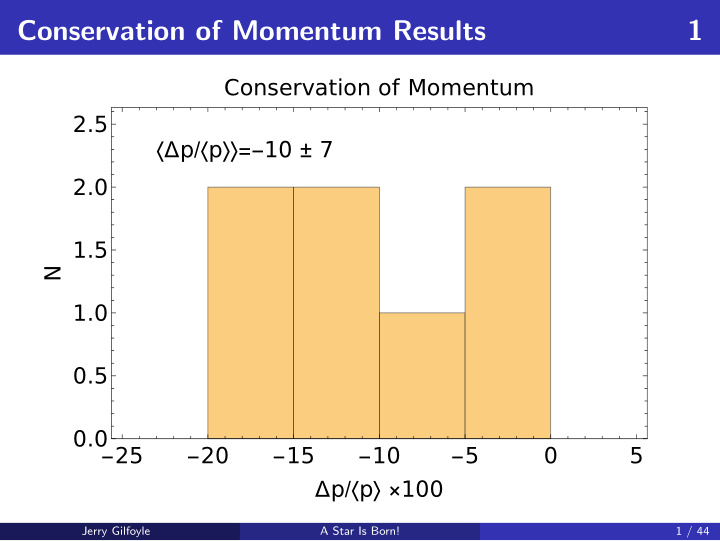



Conservation of Momentum Results 1 Conservation of Momentum 2.5 〈Δ p / 〈 p 〉〉 =- 10 ± 7 2.0 1.5 N 1.0 0.5 0.0 - 25 - 20 - 15 - 10 - 5 0 5 Δ p / 〈 p 〉 × 100 Jerry Gilfoyle A Star Is Born! 1 / 44
Some changes to Lab 28 2 1 For Activities 3b and 3d do NOT make a video of your own. Go to the course webpage here or enter the address below. https://facultystaff.richmond.edu/~ggilfoyl/genphys.html 2 Then under General Physics I (Physics 131) navigate to General Physics I links and then to the item Videos for Activities 3.b and 3.d in Momentum Conservation and Center-of-Mass . 3 There will be links for the videos for Activities 3b and 3d. Analyze these. Jerry Gilfoyle A Star Is Born! 2 / 44
Center-of-Mass Motion - Equal Massses 3 Jerry Gilfoyle A Star Is Born! 3 / 44
Center-of-Mass Motion - Equal Massses 4 Jerry Gilfoyle A Star Is Born! 3 / 44
Center-of-Mass Motion - Different Massses 5 Jerry Gilfoyle A Star Is Born! 4 / 44
Center-of-Mass Motion - Different Massses 6 Jerry Gilfoyle A Star Is Born! 4 / 44
Center-of-Mass Motion - Different Massses 7 Jerry Gilfoyle A Star Is Born! 4 / 44
Center-of-Mass Motion - Different Massses 8 0.2 Center of Mass ( m ) 0.1 0.0 - 0.1 m H x H + m L x L CM = - 0.2 m H + m L - 0.3 0.0 0.2 0.4 0.6 0.8 Time ( s ) Jerry Gilfoyle A Star Is Born! 4 / 44
Center-of-Mass 9 Jerry Gilfoyle A Star Is Born! 5 / 44
Center-of-Mass 10 Jerry Gilfoyle A Star Is Born! 6 / 44
Center-of-Mass 11 Jerry Gilfoyle A Star Is Born! 7 / 44
Center-of-Mass 12 Flying Tennis Racket Blue - x Red - y 0.4 0.2 Position 0.0 - 0.2 - 0.4 0 1 2 3 4 5 6 7 Time Jerry Gilfoyle A Star Is Born! 8 / 44
Center-of-Mass 13 Flying Tennis Racket Flying Tennis Racket 0.4 Blue - x Red - y 0.4 0.2 0.2 y Position Position 0.0 0.0 - 0.2 - 0.2 - 0.4 - 0.4 - 0.4 - 0.2 0.0 0.2 0.4 0 1 2 3 4 5 6 7 x Position Time Jerry Gilfoyle A Star Is Born! 8 / 44
A Star Is Born! 14 Jerry Gilfoyle A Star Is Born! 9 / 44
A Star Is Born! 15 Jerry Gilfoyle A Star Is Born! 9 / 44
A Star Is Born! 16 The photograph below shows a cloud of molecules called Bernard 68 (B68). It is located about 300 light-years (2 . 8 × 10 15 km ) away from us in the constellation Ophiuchus and is about 1.6 trillion kilometers across. It is made of molecules like CS , N 2 H , H 2 , and CO and is slowly rotating ( ω = 9 . 4 × 10 − 14 rad / s ). The internal gravitational attraction of B68 may make the molecular cloud collapse far enough so it will ignite the nuclear fires and B68 will begin to shine. Jerry Gilfoyle A Star Is Born! 9 / 44
A Star Is Born 17 The molecular cloud B68 in the constellation Ophiuchus is rotating with an angular speed ω = 9 . 4 × 10 − 14 rad / s . The gravitational attraction among the atoms in the cloud may make it collapse until the core is hot enough to ignite nuclear reactions and B68 will begin to shine. If the final properties of B68 are the same as our Sun, i.e. , the same mass and size, then what will be its final angular velocity and period? Assume the lost mass carries away very little angular momentum. Compare this with the angular velocity of the Sun. Is your result reasonable? Why or why not? M B 68 = 6 . 04 × 10 30 kg I B 68 = 2 . 7 × 10 54 kg − km 2 M Sun = 1 . 989 × 10 30 kg R Sun = 6 . 96 × 10 5 km T Sun = 25 . 4 d Jerry Gilfoyle A Star Is Born! 10 / 44
Rotational Quantities 18 Jerry Gilfoyle A Star Is Born! 11 / 44
Linear → Rotational Quantities 19 Linear Rotational Quantity Connection Quantity θ = s s s = r θ r ω = v T r = d θ v T v T = r ω dt α = a T r = d ω a T a T = r α dt KE = 1 2 mv 2 KE R = 1 2 I ω 2 � F = m � a τ = rF ⊥ � τ = I � α � � p = m � v L = � r × � p L = I � � ω � m i � r i r cm = � m i � Jerry Gilfoyle A Star Is Born! 12 / 44
How Fast Will the Star Spin? 20 The pulsar in the Crab nebula has a period T 0 = 0 . 033 s and this period has been observed to be increasing by ∆ T = 1 . 26 × 10 − 5 s each year. Assuming constant angular acceleration what is the expression for the angular displacement of the pulsar? What are the values of the parameters in that expression? What is the torque exerted on the pulsar? m C = 3 . 4 × 10 30 kg r C = 25 × 10 3 m Jerry Gilfoyle A Star Is Born! 13 / 44
A Pulsar 21 Jerry Gilfoyle A Star Is Born! 14 / 44
Linear → Rotational Quantities 22 Linear Rotational Quantity Connection Quantity θ = s s s = r θ r ω = v T r = d θ v T v T = r ω dt α = a T r = d ω a a T = r α dt KE = 1 2 mv 2 KE R = 1 2 I ω 2 � F = m � a τ = rF ⊥ � τ = I � α � � p = m � v L = � r × � p L = I � � ω � m i � r i r cm = � m i � Jerry Gilfoyle A Star Is Born! 15 / 44
� a → � F ∝ � F = m � 23 a Force and Motion 1 Jerry Gilfoyle A Star Is Born! 16 / 44
Torque - Rotational Equivalent of Force 24 F Jerry Gilfoyle A Star Is Born! 17 / 44
Torque on a Point Particle 25 Consider a point particle at a fixed dis- tance from the origin (attached by the ω famed massless rod or a string) that moves in a circle. F origin m r F c Jerry Gilfoyle A Star Is Born! 18 / 44
Torque on a Point Particle 26 Consider a point particle at a fixed dis- tance from the origin (attached by the ω famed massless rod or a string) that moves in a circle. F origin m r F c � τ = r � F = m � a → � F ⊥ Jerry Gilfoyle A Star Is Born! 18 / 44
Torque - Rotating a Rigid Body (a door) 27 ω r torque F hinge i Jerry Gilfoyle A Star Is Born! 19 / 44
Torque - Rotating a Rigid Body (a door) 28 ω r torque F chunks m i ∆ hinge r i Jerry Gilfoyle A Star Is Born! 20 / 44
Moments of Inertia 29 Jerry Gilfoyle A Star Is Born! 21 / 44
Linear → Rotational Quantities 30 Linear Rotational Quantity Connection Quantity θ = s s s = r θ r ω = v T r = d θ v T v T = r ω dt α = a T r = d ω a a T = r α dt KE = 1 2 mv 2 KE R = 1 2 I ω 2 � F = m � a τ = rF ⊥ � τ = I � α � p = m � v L = rp ⊥ L = I � � ω � m i � r i r cm = � m i � Jerry Gilfoyle A Star Is Born! 22 / 44
Torque - Rotational Force 31 The shield door at a neutron test fa- cility at Lawrence Livermore Labora- tory is possibly the world’s heaviest hinged door. It has a mass m = 44 , 000 kg , a rotational inertia about a vertical axis through its hinges of I = 8 . 7 × 10 4 kg − m 2 , and a (front) face width of w = 2 . 4 m . A steady force � F a = 73 N , applied at its outer edge and perpendicular to the plane of the door, can move it from rest through an angle θ = 90 ◦ in ∆ t = 75 s . What is the torque exerted by the friction in the hinges? Jerry Gilfoyle A Star Is Born! 23 / 44
Moments of Inertia 32 Jerry Gilfoyle A Star Is Born! 24 / 44
Rotational Form of � F = m � a in lab 33 Rotator Disk Applied torque Jerry Gilfoyle A Star Is Born! 25 / 44
Which One Wins? 34 A wooden disk and a metal ring have the same mass m and radius r , start from rest, and roll down identical inclined planes (see figure). Which one wins? h Jerry Gilfoyle A Star Is Born! 26 / 44
Which One Wins? 35 Jerry Gilfoyle A Star Is Born! 27 / 44
Moments of Inertia 36 Jerry Gilfoyle A Star Is Born! 28 / 44
Rolling Down an Incline 37 v d r i h r cm Jerry Gilfoyle A Star Is Born! 29 / 44
Rolling Down an Incline - 1 38 Jerry Gilfoyle A Star Is Born! 30 / 44
Rolling Down an Incline - 2 39 Jerry Gilfoyle A Star Is Born! 31 / 44
Rolling Down an Incline - 3 40 Rolling Down an Incline 40 20 y ( pixels ) 0 - 20 - 40 - 40 - 20 0 20 40 x ( pixels ) Jerry Gilfoyle A Star Is Born! 32 / 44
Which One Wins? 41 A wooden disk and a metal ring have the same mass m and radius r , start from rest, and roll down identical inclined planes (see figure). Which one wins? h Jerry Gilfoyle A Star Is Born! 33 / 44
Linear → Rotational Quantities 42 Linear Rotational Quantity Connection Quantity θ = s s s = r θ r ω = v T r = d θ v T v T = r ω dt α = a T r = d ω a a T = r α dt KE = 1 2 mv 2 KE R = 1 2 I ω 2 � F = m � a τ = rF ⊥ � τ = I � α � p = m � v L = rp ⊥ L = I � � ω � m i � r i r cm = � m i � Jerry Gilfoyle A Star Is Born! 34 / 44
Moments of Inertia 43 Jerry Gilfoyle A Star Is Born! 35 / 44
A Star Is Born 44 The molecular cloud B68 in the constellation Ophiuchus is rotating with an angular speed ω = 9 . 4 × 10 − 14 rad / s . The gravitational attraction among the atoms in the cloud may make it collapse until the core is hot enough to ignite nuclear reactions and B68 will begin to shine. If the final properties of B68 are the same as our Sun, i.e. , the same mass and size, then what will be its final angular velocity and period? Assume the lost mass carries away very little angular momentum. Compare this with the angular velocity of the Sun. Is your result reasonable? Why or why not? M B 68 = 6 . 04 × 10 30 kg I B 68 = 2 . 7 × 10 54 kg − km 2 M Sun = 1 . 989 × 10 30 kg R Sun = 6 . 96 × 10 5 km T Sun = 25 . 4 d Jerry Gilfoyle A Star Is Born! 36 / 44
Recommend
More recommend