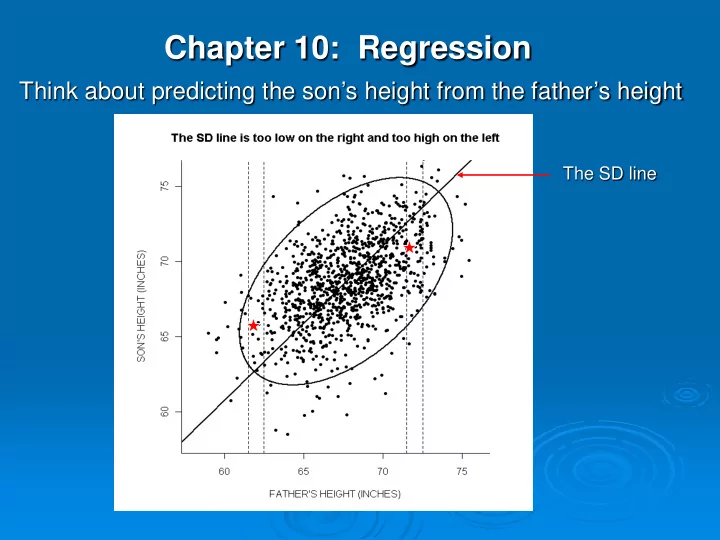
Chapter 10: Regression Think about predicting the sons height from - PowerPoint PPT Presentation

Chapter 10: Regression Think about predicting the son’s height from the father’s height The SD line

the SD line the regression line

The regression line is used to predict the y variable when we know the x variable. The regression line: • goes through the point of averages (ave X , ave Y ) • with slope = r (SD Y ) SD X

To draw the regression line: • go to the point of averages and put a dot • move to the right SD X and up r (SD Y ), put another dot (if r is negative, move down) • join the dots

Midterm: ave = 75 SD = 10 r = 0.7 Final: ave = 70 SD = 12 Draw the regression line

To predict or estimate the value of y when you know the value of x: Find out how many SDs it is above or below 1. the average in the x variable. Multiply the answer to step 1 by r. 2. The answer to step 2 tells you how many SDs 3. it is above or below the average in the y variable.

Example 1. Hanes, men 18-24: average height =70”, SD = 3” average weight = 162lb, SD = 30lb r = 0.47 Approximately what is the average weight of men who are 76” tall? a) 64” tall? b) 69” tall? c) 73” tall? d)

Example 2: Midterm: ave = 75 SD = 10 r = 0.7 Final: ave = 70 SD = 12 Estimate the final exam score for someone who got 87 on the midterm

Example 3: For the men aged 18-24 in the HANES sample, the relationship between height and systolic blood pressure can be summarized as follows: Average height ≈ 70”, SD ≈ 3” Average b.p. ≈ 124mm, SD ≈ 14mm r = -0.2 Estimate the average blood pressure of men who were 6 feet tall.

Another example: heights and weights SD line regression line

CAUTION!

Example 4: Midterm: ave = 75 SD = 10 r = 0.7 Final: ave = 70 SD = 12 Estimate the final exam score for someone who got 87 on the 1. midterm. Estimate the midterm score for someone who got 80 on the final. 2.

There are two regression lines! Regression line for predicting MIDTERM SD line Regression line for predicting FINAL

FINAL FINAL FINAL MIDTERM MIDTERM

The Regression Effect In test-retest situations, people with low scores tend to improve and people with high scores tend to do worse. WHY? Chance Error!

The Regression Effect Observed value = true value + chance error Positive or negative Example: IQ test scores, average = 100, SD = 15. If someone scores 140 on their first test, they probably got a _________ chance error. If someone scores 80 on their first test, they probably got a _________ chance error.

The Regression FALLACY Attributing the regression effect to something other than chance error. Example: A group of people get their blood pressure measured. Those that have high blood pressure return and have their blood pressure measured again. We expect their second measurements to have a smaller average than their first measurements, due to the regression effect. Attributing this apparent drop to a change in behavior is the regression fallacy.