Car-Like Robot: e.g., lie in free space How to Park a Car? - PDF document

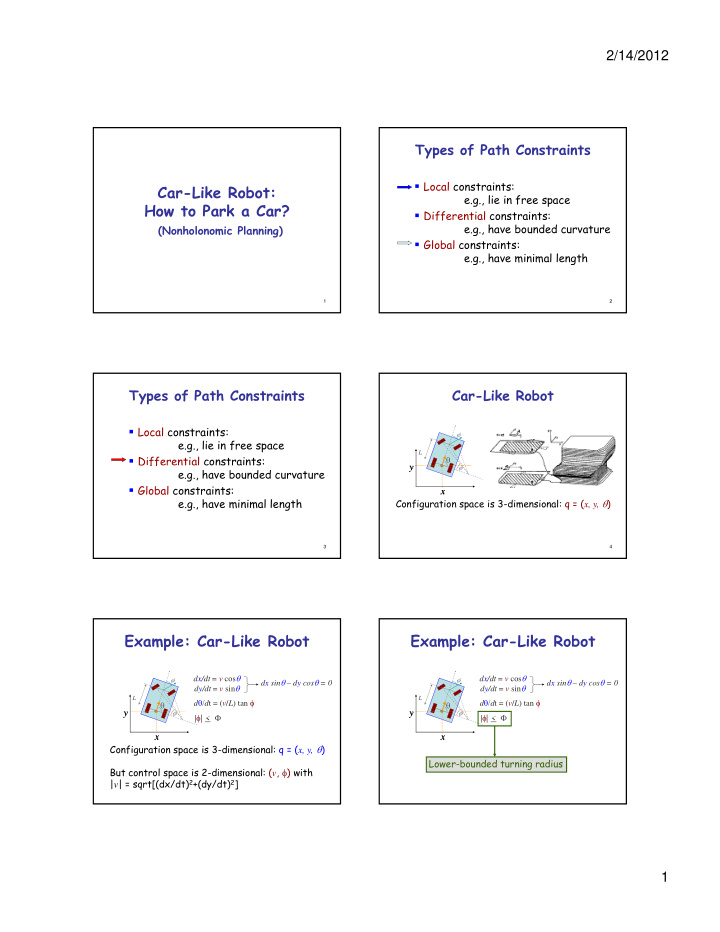
2/14/2012 Types of Path Constraints � Local constraints: Car-Like Robot: e.g., lie in free space How to Park a Car? � Differential constraints: ff e.g., have bounded curvature (Nonholonomic Planning) � Global constraints: e.g., have minimal length 1 2 Types of Path Constraints Car-Like Robot � Local constraints: e.g., lie in free space L � Differential constraints: ff θ y e.g., have bounded curvature � Global constraints: x e.g., have minimal length Configuration space is 3-dimensional: q = ( x, y, θ ) 3 4 Example: Car-Like Robot Example: Car-Like Robot dx/dt = v cos θ dx/dt = v cos θ dx sin θ – dy cos θ = 0 dx sin θ – dy cos θ = 0 dy/dt = v sin θ dy/dt = v sin θ L L d θ/ d t = ( v / L ) tan φ d θ/ d t = ( v / L ) tan φ θ θ y y |φ | < Φ | | |φ | < Φ x x Configuration space is 3-dimensional: q = ( x, y, θ ) Lower-bounded turning radius But control space is 2-dimensional: ( v , φ ) with | v | = sqrt[(dx/dt) 2 +(dy/dt) 2 ] 1

2/14/2012 How Can This Work? How Can This Work? Tangent Space/Velocity Space Tangent Space/Velocity Space θ θ (x,y, θ ) (x,y, θ ) ( dx,dy,d θ ) ( dx,dy,d θ ) L L θ θ y y x x dx/dt = v cos θ dx/dt = v cos θ y y dy/dt = v sin θ dy/dt = v sin θ ( dx,dy ) ( dx,dy ) d θ/ d t = ( v / L ) tan φ d θ/ d t = ( v / L ) tan φ θ θ x x dx sin θ – dy cos θ = 0 |φ | < Φ | | |φ | < Φ Type 2 Maneuver Type 1 Maneuver CYL(x,y, δθ , η ) η (x1, y1, θ 0+ δθ ) d η δθ q ρ (x,y, θ 0 ) (x y θ ) δθ (x3, y3, θ 0) dq η = 2 ρ tan δθ (x,y) (x0, y0, θ 0) δθ dq d = 2 ρ (1/ cos δθ − 1) > 0 ρ When δθ � 0, so does d (x2, y2, θ 0+ δθ ) and the cylinder becomes arbitrarily small � Allows sidewise motion � Allows pure rotation 10 (x1, y1, θ 0+ δθ ) Combination Combination d (x3, y3, θ 0) dq (x0, y0, θ 0) dq (x2, y2, θ 0+ δθ ) 11 12 2

2/14/2012 Coverage of a Path by Cylinders Path Examples θ q + q’ y x Path created ignoring the car constraints 13 14 Drawbacks Reeds and Shepp Paths � Final path can be far from optimal � Not applicable to car that can only move forward (e.g., think of an airplane) 15 Example of Generated Path Reeds and Shepp Paths Holonomic CC|C 0 CC|C C|CS 0 C|C Given any two configurations, the shortest RS paths between them is also the shortest path Nonholonomic 3

2/14/2012 Other Technique: Other Technique: Control-Based Sampling Control-Based Sampling dx sin θ – dy cos θ = 0 dx/dt = v cos θ Indexing array: dy/dt = v sin θ A 3-D grid is placed over the d θ/ d t = ( v / L ) tan φ d θ/ d t = ( v / L ) tan φ configuration space Each milestone configuration space. Each milestone falls into one cell of the grid. A |φ | < Φ | maximum number of milestones is allowed in each cell (e.g., 2 or 3). 1. Select a node m Asymptotic completeness: 2. Pick v , φ , and dt If a path exists, the planner is 3. Integrate motion from m guaranteed to find one if the � new configuration resolution of the grid is fine enough. 19 Application Computed Paths Tractor-trailer Car That Can Only Turn Left ϕ m ax = 45 o , ϕ m in = 22.5 o ϕ m ax = 45 o 21 22 Architectural Design: Other “Similar” Robots/Moving Verification of Building Code Objects (Nonholonomic) Rolling-with-no-sliding � contact (friction), e.g.: car, bicycle, roller skate Submarine, airplane S b i i l � Conservation of angular � momentum: satellite robot, under-actuated robot, cat Why is it useful? - Fewer actuators: design simplicity, less weight - Convenience (think about driving a car with 3 controls!) 23 24 C. Han 4