Bel ( x t ) = P ( z t | x t ) P ( x t | u t 1 , x t 1 ) Bel ( x t - PDF document

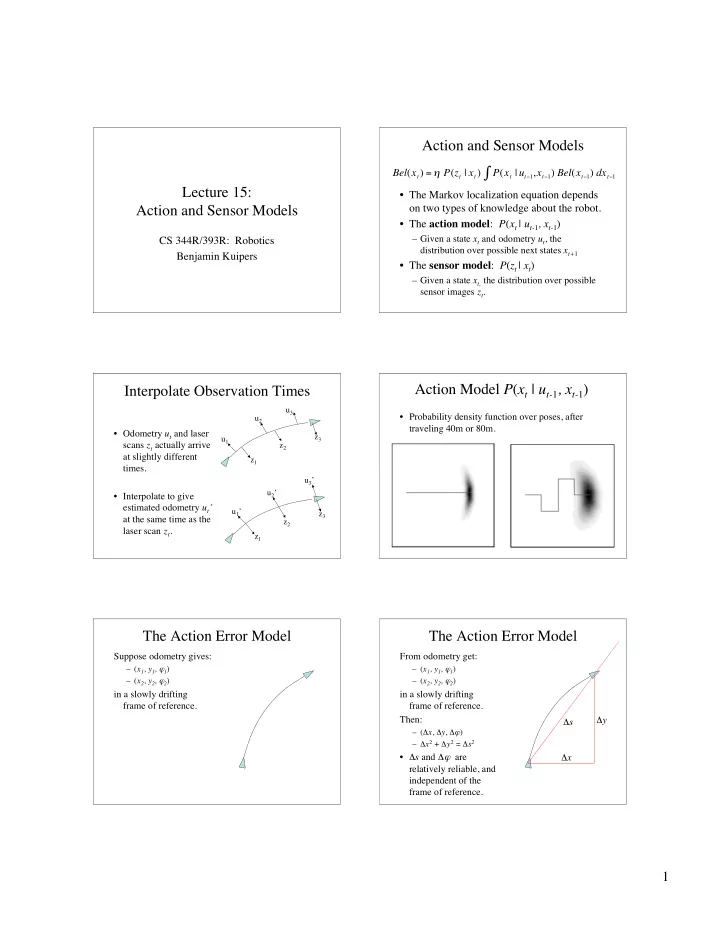
Action and Sensor Models � Bel ( x t ) = � P ( z t | x t ) P ( x t | u t � 1 , x t � 1 ) Bel ( x t � 1 ) dx t � 1 Lecture 15: • The Markov localization equation depends on two types of knowledge about the robot. Action and Sensor Models • The action model : P ( x t | u t- 1 , x t- 1 ) – Given a state x t and odometry u t , the CS 344R/393R: Robotics distribution over possible next states x t+ 1 Benjamin Kuipers • The sensor model : P ( z t | x t ) – Given a state x t, the distribution over possible sensor images z t . Action Model P ( x t | u t- 1 , x t- 1 ) Interpolate Observation Times u 3 • Probability density function over poses, after u 2 traveling 40m or 80m. • Odometry u t and laser z 3 u 1 scans z t actually arrive z 2 at slightly different z 1 times. u 3 ’ u 2 ’ • Interpolate to give estimated odometry u t ′ u 1 ’ z 3 at the same time as the z 2 laser scan z t . z 1 The Action Error Model The Action Error Model Suppose odometry gives: From odometry get: – ( x 1 , y 1 , ϕ 1 ) – ( x 1 , y 1 , ϕ 1 ) – ( x 2 , y 2 , ϕ 2 ) – ( x 2 , y 2 , ϕ 2 ) in a slowly drifting in a slowly drifting frame of reference. frame of reference. Then: Δ y Δ s – ( Δ x , Δ y , Δ ϕ ) – Δ x 2 + Δ y 2 = Δ s 2 • Δ s and Δ ϕ are Δ x relatively reliable, and independent of the frame of reference. 1

The Action Error Model The Action Error Model From odometry get: From odometry get: Δ ϕ− α – ( x 1 , y 1 , ϕ 1 ) – ( x 1 , y 1 , ϕ 1 ) – ( x 2 , y 2 , ϕ 2 ) – ( x 2 , y 2 , ϕ 2 ) Δ ϕ Δ ϕ in a slowly drifting frame – ( Δ x , Δ y , Δ ϕ ) of reference. – Δ x 2 + Δ y 2 = Δ s 2 Then: – α = atan2( Δ y , Δ x ) −ϕ 1 Δ y Δ y Δ s Δ s – ( Δ x , Δ y , Δ ϕ ) • Model the action as: – Δ x 2 + Δ y 2 = Δ s 2 – Turn( α ) α α and: – Travel( Δ s ) Δ x Δ x – α = atan2( Δ y , Δ x ) −ϕ 1 – Turn( Δ ϕ− α ) – (Measure angle counter- clockwise from x -axis) The Action Error Model Tune the Action Error Model • Model the action as: • Model the action as: • Compute error Δ ϕ− α between: – Turn( α + ε 1 ) – Turn( α + ε 1 ) – Travel( Δ s + ε 2 ) – Travel( Δ s + ε 2 ) – odometry observed – Turn( Δ ϕ− α + ε 3 ) – Turn( Δ ϕ− α + ε 3 ) – odometry corrected by localization. where where • Divide by turn or − ε 1 ~ N (0, k 1 α ) − ε 1 ~ N (0, k 1 α ) Δ s travel magnitude. − ε 2 ~ N (0, k 2 Δ s ) − ε 2 ~ N (0, k 2 Δ s ) • Compute standard − ε 3 ~ N (0, k 1 ( Δ ϕ− α )) − ε 3 ~ N (0, k 1 ( Δ ϕ− α )) α deviations • This combines three • Tune the model by – k 1 = 1.0 Gaussian errors. finding k 1 and k 2 . – k 2 = 0.4 – Std dev proportional to action magnitude The Action Model P ( x t | u t- 1 , x t- 1 ) Sensor Model P ( z t | x t ) • Given a small motion u t- 1 = ( α , Δ s , Δ ϕ−α ) • For a given range measurement at a given location x t in the map: � x t � � x t � 1 � � ( � s + � 2 )cos( � t � 1 + � + � 1 ) � � � � � � � y t = y t � 1 + ( � s + � 2 )sin( � t � 1 + � + � 1 ) � � � � � � � � � � � � � t � t � 1 � � + � 1 + � 3 � � � � � � where − ε 1 ~ N (0, k 1 α ) − ε 2 ~ N (0, k 2 Δ s ) − ε 3 ~ N (0, k 1 ( Δ ϕ− α )) 2

Laser Rangefinder Scan z t Density P ( z t | x t ) by Location Q: Didn’t we use log odds before? Computing P ( z t | x t ) • Yes, but that was in the occupancy grid. • Image probabilities are too small to be – It is useful as a way to represent P ( occ ( i,j )) meaningful: – Certainty on either side of ignorance 180 � P ( z t | x t ) = P ( ray ( i ) = d i | x t ) i = 1 • Here, we’re doing Markov localization. • But log probabilities can be accumulated � Bel ( x t ) = � P ( z t | x t ) P ( x t | u t � 1 , x t � 1 ) Bel ( x t � 1 ) dx t � 1 180 � log P ( z t | x t ) = log P ( ray ( i ) = d i | x t ) • We need to compare values of P ( z t | x t ). i = 1 – without numerical underflow. – Odds would just be a distraction – Log helps us avoid numerical underflow Computing log P ( ray ( i ) = d i | x t ) P ( ray ( i ) = d i | x t ) • If ray(i) terminates at the first obstacle: log P ( ray ( i )= d i | x t ) = − 4 • If ray(i) terminates before an obstacle: log P ( ray ( i )= d i | x t ) = − 8 • If ray(i) terminates after an obstacle: log P ( ray ( i )= d i | x t ) = − 12 • Add them up for i =1 to 180. 180 � log P ( z t | x t ) = log P ( ray ( i ) = d i | x t ) i = 1 – log P ( z t | x t ) totals between − 720 and − 2160 – Exponentiating would give zero! 3

Avoiding Numerical Underflow How Can We Normalize? • We’re summing many negative log values � Bel ( x t ) = � P ( z t | x t ) P ( x t | u t � 1 , x t � 1 ) Bel ( x t � 1 ) dx t � 1 180 � log P ( z t | x t ) = log P ( ray ( i ) = d i | x t ) • To compute η , we must add un-normalized i = 1 • Exponentiating will just give us zero! values, each with log much less than -720. – Exponentiating would give zero for every one! • But we’re just going to normalize, next. • Solution: – So multiply by a constant, and normalize it out. – Adjust by adding the largest log P to all values. – I.e., add a constant to each log P ( z t | x t ) – Exponentiate. The largest values remain non-zero. • Shift the largest log P ( z t | x t ) value to zero. – Then normalize, which divides out the adjustment. – I.e., add max log P ( z t | x t ) to each value. – Underflow only eliminates negligible values. – Then we have values of P ( z t | x t ) we can normalize. Estimate P ( z t | x t ) with Correlation An Approximation to Scan Matching • Given a pose hypothesis x t , build a “sensor • Ignores visibility problems. patch” (new map) from scan z t . • Compute correlation between sensor patch and map grid. Fast Approximate Correlation Potential Problems with P ( z t | x t ) • Let c i be a cell in the sensor patch – If the endpoint of a laser ray hits, c i = 1. • Grid cells are only partially occupied. – Otherwise, c i = 0. • The corresponding cell in the map grid is m i – Should we model the porosity of each cell? and p ( m i ) is its occupancy probability. � Corr ( z t , x t ) = c i p ( m i ) i Bel ( x t ) = � Corr ( z t , x t ) Bel � ( x t ) • Orders-of-magnitude speed improvement [Konolige & Chou, IJCAI-99]. 4

Future Attractions • Particle filter algorithm. • Landmark-based mapping. • Topological mapping. 5