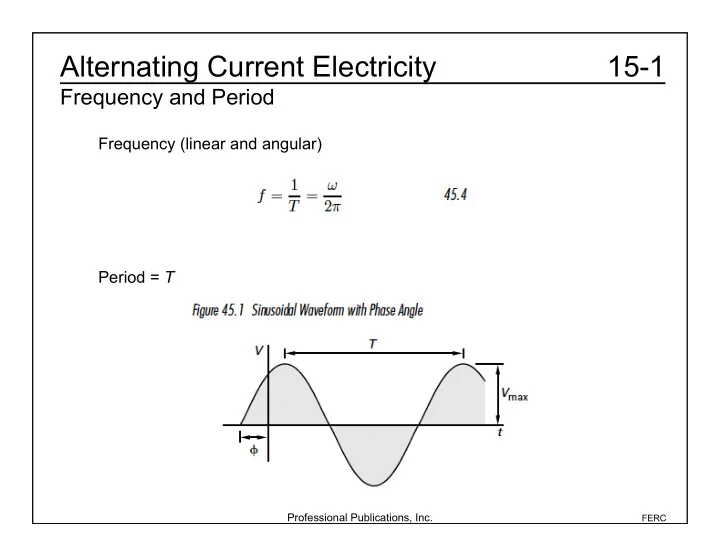

Alternating Current Electricity 15-1 Frequency and Period Frequency (linear and angular) Period = T Professional Publications, Inc. FERC
Alternating Current Electricity 15-2a Average Value Square wave, positive pulse = negative pulse: X ave = 0 Pulse pattern, positive, all the same: X ave = tX max T where t is the duration of the pulse and T is the period. 1 2 X max Sawtooth: X ave = Symmetrical triangular wave: X ave = 0 Professional Publications, Inc. FERC
Alternating Current Electricity 15-2b Average Value Example (FEIM): A plating tank with an effective resistance of 100 Ω is connected to the output of a full-wave rectifier. The applied voltage is sinusoidal with a maximum of 170 V. How long does it take to transfer 0.005 faradays? V ave = 2 V max = (2)(170 V) = 108.2 V � � I ave = V ave R = 108.2 V 100 � = 1.082 A (0.005 F) 96,487 A � s � � � � F t = q � � = I ave 1.082 A = 446 s Professional Publications, Inc. FERC
Alternating Current Electricity 15-3a Effective or Root-Mean-Squared (RMS) Value Effective value of an alternating Pulse pattern, positive, all the same: waveform: t X rms = T X max where t is the duration of the pulse and T is the period. For a sinusoidal waveform, X rms = 1 Symmetrical triangular: X max 3 For a half-wave sinusoidal waveform, X rms = 1 Sawtooth: X max 3 Professional Publications, Inc. FERC
Alternating Current Electricity 15-3b Effective or Root-Mean-Squared (RMS) Value Example 1 (FEIM): A 170 V (maximum value) sinusoidal voltage is connected across a 4 Ω resistor. What is the power dissipated by the resistor? V rms = V max = 170 V = 120.2 V 2 2 2 ( 120.2 V ) P = V rms 2 3 W = 3.61 � 10 R = 4 � Professional Publications, Inc. FERC
Alternating Current Electricity 15-3c1 Effective or Root-Mean-Squared (RMS) Value Example 2 (FEIM): What is the I rms value for the following waveform? 2 (A) 4 I 3 (B) 4 I 10 I (C) 4 3 (D) 2 I Professional Publications, Inc. FERC
Alternating Current Electricity 15-3c2 Effective or Root-Mean-Squared (RMS) Value 2 1 1 2 dt + 1 � � I T T T I rms = ( I ( t )) 2 I dt � � � = 2 � � T T T T 2 0 0 � � 2 � � � � � � � � � � I 2 T � + 1 � I 2 I 2 I 2 � T T � T ( ) T = = 2 + � � � � � � T 2 T 4 4 T 2 � � � � � � � � � � 2 I 2 + I 2 2 5 10 2 = 8 I I = 8 = 4 Therefore, the answer is (C). Professional Publications, Inc. FERC
Alternating Current Electricity 15-3d Effective or Root-Mean-Squared (RMS) Value Example 3 (FEIM): A sinusoidal AC voltage with a value of V rms = 60 V is applied to a purely resistive circuit. What steady-state voltage would dissipate the same power as the AC voltage? (A) 30 V (B) 42 V (C) 60 V (D) 85 V The answer is right in the problem statement. Since the voltage is given as an rms value, the equivalent DC voltage is simply 60 V. Therefore, the answer is (C). Professional Publications, Inc. FERC
Alternating Current Electricity 15-4 Phasor Transforms Phase angle = θ – φ φ as the angle between the reference and voltage θ as the angle between the reference and current If the phase angle is positive, the signal is called “leading” or “capacitive.” If the phase angle is negative, the signal is called “lagging” or “inductive.” If the phase angle is zero, the signal is called “in phase.” Professional Publications, Inc. FERC
Alternating Current Electricity 15-5a Impedance Definitions Impedance: Resistor: Capacitor: Inductor: Professional Publications, Inc. FERC
Alternating Current Electricity 15-5b1 Impedance Example (FEIM): For the following circuit: (a) What is the impedance in polar form? (b) Is the current leading or lagging? (c) What is the voltage across the inductor? Professional Publications, Inc. FERC
Alternating Current Electricity 15-5b2 Impedance � � Z = 3 � + j 400 1 1 � 3 H) – j (a) (2.5 � 10 + 9 �� 40 ° � � s � � 400 1 � 3 F) � � (625 � 10 � � s � � = 3 � + j 1 �� j 4 � + (9 � )cos40 °+ ( j 9 � )sin40 ° = 3 � + 6.894 � + j (1 �� 4 � + 5.785 � ) = 9.894 � + j 2.785 � 2 + (2.785 � ) 2 = 10.28 � Z = (9.894 � ) � 1 imaginary � � Phase angle = tan � � real � � � � � 1 2.785 � = tan � = 15.72 ° � 9.894 � � � Z = 10.28 �� 15.72 ° Professional Publications, Inc. FERC
Alternating Current Electricity 15-5b3 Impedance � � I = V 160V � 0 ° (b) � = 16.56A �� 15.72 ° Z = � 10.28 �� 15.72 ° � � Therefore, the current is lagging (ELI). (c) V L = I Z L = (15.56 A �� 15.72 ° )(1 � � 90 ° ) = 15.56 V � 74.28 ° Professional Publications, Inc. FERC
Alternating Current Electricity 15-6 Admittance Multiplying by the complex conjugate, Professional Publications, Inc. FERC
Alternating Current Electricity 15-7 Ohm’s Law for AC Circuits Example (FEIM): What is the current in the capacitor in the following circuits? (a) Z = 2 �� j 4 � = 4.47 � �� 63.4 ° I = V 180 V � 0 ° 4.47 � �� 63.4 ° = 40.3 A � 63.4 ° Z = (b) Z c = 0.25 � �� 90 ° I = V 180 V � 0 ° 0.25 � �� 90 ° = 720 A � 90 ° = Z c Professional Publications, Inc. FERC
Alternating Current Electricity 15-8a Complex Power P : real power (W) Q : reactive power (VAR) S : apparent power (VA) • Power Factor: • Real Power: • Reactive Power: Professional Publications, Inc. FERC
Alternating Current Electricity 15-8b1 Complex Power Example (FEIM): For the following circuit, find the (a) real power, and (b) reactive power. (c) Draw the power triangle. P = V R R = (120 V) 2 2 (a) The real power is: = 1440 W 10 � Q = V L 2 = (120 V) 2 (b) The reactive power is: = 3600 VAR X L 4 � Professional Publications, Inc. FERC
Alternating Current Electricity 15-8b2 Complex Power (c) The power triangle is: In this example, the impedance of the inductor has a lagging Current so the current has a negative phase angle. The complex conjugate of the current has a positive phase angle, so the reactive power, Q , is positive and the power triangle is in the first quadrant. For a leading current (which has a positive phase angle compared to the voltage) the power triangle has a negative imaginary part and a negative power angle, so it is in the fourth quadrant. Professional Publications, Inc. FERC
Alternating Current Electricity 15-9a Resonance Series Resonance Quality Factor: Bandwidth: R = X : � 1/2power = � 0 ± 1 2BW Half-power point is when Parallel Resonance Quality Factor: Bandwidth: R = X : � 1/2power = � 0 ± 1 Half-power point is when 2 Q Professional Publications, Inc. FERC
Alternating Current Electricity 15-9b1 Resonance Example (FEIM): For the following circuit, find (a) the resonance frequency (rad/s) (b) the half-power points (rad/s) (c) the peak current (at resonance) (d) the peak voltage across each component at resonance 1 1 6 rad (a) = 5 � 10 � 0 = = � 6 H)(200 � 10 � 12 F) s LC (200 � 10 Professional Publications, Inc. FERC
Alternating Current Electricity 15-9b2 Resonance 2 power = � 0 ± 1 (b) 2BW � 1 = � 0 ± R 6 rad 50 � 2 L = 5 � 10 s ± � 6 H) (2)(200 � 10 6 rad = 5.125 � 10 6 , 4.875 � 10 s At resonance, Z = R , I (resonance) = V R = 20 V � 0 ° (c) = 0.4 A � 0 ° 50 � (d) V R = I 0 R = 0.4 A � 0 ° ( ) 50 � ( ) = 20 V � 0 ° � � 6 rad � 6 H) � 90 ° V L = I 0 X L = I 0 j � L = (0.4 A � 0 ° ) 5 � 10 (200 � 10 � � s � � = 400 � 90 ° V C = � V L = 400 V �� 90 ° Professional Publications, Inc. FERC
Alternating Current Electricity 15-9c Resonance Example (FEIM): A parallel resonance circuit with a 10 Ω resistor has a resonance frequency of 1 MHz and bandwidth of 10 kHz. What resistor value will increase the BW to 20 kHz? � 0 RC = 1 BW = � 0 � 0 Q = RC C remains the same, so to double the BW. R new = 1 2 R old = 5 � Professional Publications, Inc. FERC
Alternating Current Electricity 15-10a Transformers Professional Publications, Inc. FERC
Alternating Current Electricity 15-10b Transformers Example 1 (FEIM): What is the voltage V 3 ? Disregard losses. (A) 45 V (B) 65 V (C) 75 V (D) 90 V V 2 = N 2 V 3 = N 3 120 V V 2 N 1 N A � � � � � � � � V 3 = N 3 � N 2 ) = 300 � 50 � 120 V ( � 120 V ( ) = 90 V � � � � N A N 1 100 200 � � � � � � � � Therefore, the answer is (D). Professional Publications, Inc. FERC
Alternating Current Electricity 15-10c Transformers Example 2 (FEIM): What is the total impedance in the primary circuit? Assume an ideal transformer. 2 � � 50 Z total = Z p + Z = (12 � + j 4 � ) + 3 � + j � � � 100 � � = 4 � + 3 � + j (1 � + 1 � ) = 7 � + j 2 � Professional Publications, Inc. FERC
Alternating Current Electricity 15-11a Rotating Machines Synchronous Machines 1. Synchronous motors 2. Synchronous generators Professional Publications, Inc. FERC
Recommend
More recommend