


TU/e Algorithms (2IL15) – Lecture 6 Algorithms (2IL15) – Lecture 6 ALL-PAIRS SHORTEST PATHS w 1,k … a i,1 … a i,n = b i,k w n,k 1
TU/e Algorithms (2IL15) – Lecture 6 Previous lecture: Single-Source Shortest Paths Dijkstra’s algorithm works only for non-negative edge weights running time Θ ( | V | log | V | + | E | ) Bellman-Ford algorithm can handle negative edge weights, works even for negative-weight cycles running time Θ ( | V | ∙ | E | ) Today: the All-Pairs Shortest-Path Problem 2
TU/e Algorithms (2IL15) – Lecture 6 All-Pairs Shortest Paths If we only have non-negative edge-weights: Run Dijkstra’s algorithm |V| times, once with each vertex as source running time Θ ( | V 2 | log | V | + |V| ∙ | E | ) What to do if we also have negative edge weights? 3
TU/e Algorithms (2IL15) – Lecture 6 adjacency-matrix representation weighted, directed graph 1 2 3 4 5 6 7 1 0 2 v 4 − 2 v 3 2 0 4 1 v 1 0 -2 3 1 2 v 5 2 0 1 4 v 6 0 5 4 2.3 1 2 0 2.3 6 v 2 0 7 v 7 M [ i,j ] = 0 if i = j w(v i ,v j ) if i ≠ j and edge (v i ,v j ) exists; w(v i ,v j ) is weight of (v i ,v j ) 8 if edge (v i ,v j ) does not exist 4
TU/e Algorithms (2IL15) – Lecture 6 Warm-up/Recap: Bellman-Ford via dynamic programming 5
TU/e Algorithms (2IL15) – Lecture 6 5 steps in designing dynamic-programming algorithms 1. define subproblems [#subproblems] 2. guess first choice [#choices] 3. give recurrence for the value of an optimal solution [time/subproblem treating recursive calls as Θ (1))] i. define subproblem in terms of a few parameters ii. define variable m [..] = value of optimal solution for subproblem iii. relate subproblems by giving recurrence for m [..] 4. algorithm: fill in table for m [..] in suitable order (or recurse & memoize) 5. solve original problem Running time: #subproblems * time/subproblem Correctness: (i) correctness of recurrence: relate OPT to recurrence (ii) correctness of algorithm: induction using (i) 6
TU/e Algorithms (2IL15) – Lecture 6 Single-Source Shortest Paths: structure of optimal solution V = { v 1 , v 2 , … , v n } s = v 1 shortest path from s to v i with m edges shortest path from s to v j with m−1 edges v j v i v 1 Subproblem: For each vertex v i compute shortest path from s to v i with at most m edges Define variable: L(i,m) = length of shortest path from s to v i with at most m edges Recursive formula: if i =1 and m = 0 0 8 Note: here L ( i,m ) = if 1 < i ≤ n − 1 and m = 0 adjacency matrix, min { L ( j , m −1) + w ( v j , v i ) } if 0 < m ≤ n −1 but Bellman-Ford 1≤ j ≤ n uses adjacency list 7
TU/e Algorithms (2IL15) – Lecture 6 Single-Source Shortest Paths: dynamic-programming solution Recursive formula: 0 if i =1 and m = 0 L ( i,m ) = if 1 < i ≤ n − 1 and m = 0 8 min { L ( j , m −1) + w ( v j , v i ) } if 0 < m ≤ n − 1 1≤ j ≤ n m 0 n-1 0 1 8 8 8 8 solution to original problem i is in last column 8 8 8 8 8 n 8
TU/e Algorithms (2IL15) – Lecture 6 Single-Source Shortest Paths: dynamic-programming solution Recursive formula: 0 if i =1 and m = 0 L ( i,m ) = if 1 < i ≤ n − 1 and m = 0 8 min { L ( j , m −1) + w ( v j , v i ) } if 0 < m ≤ n − 1 1≤ j ≤ n SSSP-DynamicProgramming ( G,s ) // G = ( V,E ) with V = { v 1 , v 2 , … , v n } and s = v 1 L [ 1,0 ] ← 0 1. O(n 3 ) running time: for i ← 2 to n do L [ i,0 ] ← 8 2. O(n 2 ) storage: for m ← 1 to n − 1 3. Note: Bellman-Ford do for i ← 1 to n 4. actually runs in O(|V||E|) time using do L [ i,m ] ← min { L ( j , m −1) + w ( v j , v i ) } 5. 1≤ j ≤ n O(|V|) space. How to check if a negative- after algorithm: L [ i,n-1 ] = δ (v 1 ,v i ) for all i weight cycle is reachable? 9
TU/e Algorithms (2IL15) – Lecture 6 Now adapt to all-pairs shortest paths V = { v 1 , v 2 , … , v n } shortest path from v i to v k with m edges shortest path from v i to v j with m−1 edges v j v k v i Subproblem: For each pair v i ,v k compute shortest path from v i to v k with at most m edges Define variable: L(i,k,m) = length of shortest path from v i to v k with at most m edges Recursive formula: 0 if i = k and m = 0 L ( i,k,m ) = if i ≠ k and m = 0 8 min { L ( i , j , m −1) + w ( v j , v k ) } if 0 < m ≤ n −1 1≤ j ≤ n 10
TU/e Algorithms (2IL15) – Lecture 6 All-Pairs Shortest Paths: dynamic-programming solution Recursive formula: 0 if i = k and m = 0 L ( i,k,m ) = if i ≠ k and m = 0 8 min { L ( i , j , m −1) + w ( v j , v k ) } if 0 < m ≤ n −1 1≤ j ≤ n Slow-All-Pairs-Shortest-Paths ( G,s ) O(n 4 ) running time: for i ← 1 to n 1. O(n 3 ) storage: do for k ← 1 to n 2. do L [ i,k,0 ] ← 8 3. for i ← 1 to n do L [ i,i,0 ] ← 0 4. for m ← 1 to n − 1 5. NB: still need to check for do for i ← 1 to n 6. negative-weight cycles do for k ← 1 to n 7. do L [ i,k,m ] ← min { L ( i , j , m −1) + w ( v j , v k ) } 8. 1≤ j ≤ n 11
TU/e Algorithms (2IL15) – Lecture 6 All-Pairs Shortest Paths: slightly different formulation New recursive formula: L ( i,k,m ) = w ( v j , v k ) if m = 1 min { L ( i , j , m −1) + w ( v j , v k ) } if 1 < m ≤ n −1 1≤ j ≤ n Slow-All-Pairs-Shortest-Paths ( G,s ) L ← W // W = matrix of edge weights : W [ i,j ] = w ( v j , v j ) 1. for m ← 2 to n − 1 2. do L ← Extend -Shortest-Paths ( L, W) 3. Extend-Shortest-Paths ( L,W ) 1. Let B be a new n x n matrix for i ← 1 to n 2. do for k ← 1 to n 3. do B [ i,k ] ← min { L ( i , j ) + w ( v j , v k ) } 4. 1≤ j ≤ n 5. return B 12
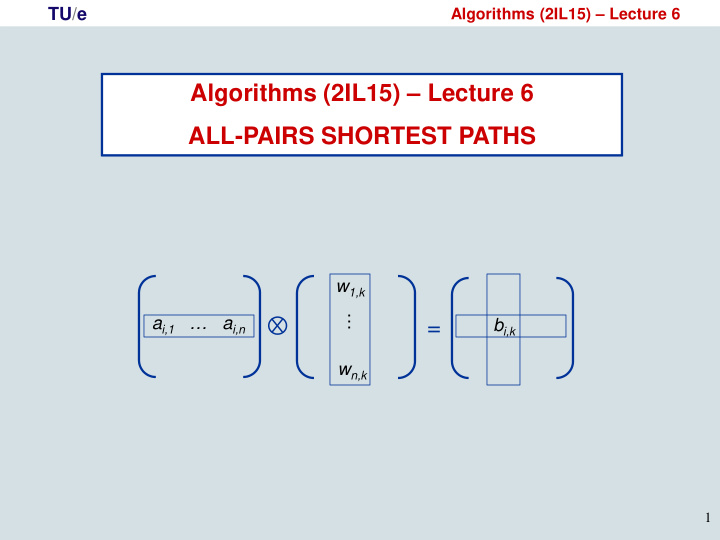
TU/e Algorithms (2IL15) – Lecture 6 All-Pairs Shortest Paths: relation to matrix multiplication Recursive formula: L ( i,k,m ) = w ( v j , v k ) if m = 1 min { L ( i , j , m −1) + w ( v j , v k ) } if 1 < m ≤ n −1 1≤ j ≤ n A = matrix with a i,k = L [ i,k,m −1 ] = min length of path with m− 1 edges from v i to v k W = matrix such that w i,k = w ( v i , v k ) = weight of edge w ( v i , v k ) B = matrix with b i,k = L [ i,k,m ] = min length of path with m edges from v i to v k w 1,k b i,k = min ( a i,k + w i,k ) … a i,1 … a i,n = b i,k 1≤ j ≤ n w n,k replacing “min” by “∑” and “+” by “∙” gives normal matrix multiplication 13
TU/e Algorithms (2IL15) – Lecture 6 Let’s change notation for the matrices: D (m) = matrix with d i,k = L [ i,k,m ] = min length of path with m edges from v i to v k W = matrix such that w i,k = w ( v i , v k ) = weight of edge w ( v i , v k ) Then D (m) = D (m-1) W = ( D (m-2) W ) W = D (1) W W … W is associative m−1 times = W m 14
TU/e Algorithms (2IL15) – Lecture 6 Conclusion Solving the All-Pairs Shortest Paths Problem is equivalent to computing the matrix product W n-1 with the -multiplication operator. Extend-Shortest-Paths ( L,W ) computes matrix “product” L W We can use this insight to speed up the algorithm: repeated squaring: W → W 2 = W W → W 4 = W 2 W 2 → … Extend-Shortest-Paths W m = W n-1 for all m ≥ n−1 if there are no negative-weight cycles 15
TU/e Algorithms (2IL15) – Lecture 6 New algorithm Faster-All-Pairs-Shortest-Paths ( W ) \\ W is matrix with edge weights 1. L ← W; n ← number of rows of W // n = | V | 2. m ← 1 3. while m < n -1 4. do // Invariant: L = W m 5. L ← Extend -Shortest-Paths ( L,L ) // L ← L L 6. m ← 2 m 7. return L running time = O ( n 3 ) x number of times line 5 is executed = O ( n 3 log n ) … still need to check for negative-weight cycles. 16
TU/e Algorithms (2IL15) – Lecture 6 shortest path from v i to v k with m edges shortest path from v i to v j with m−1 edges v j v k v i Theorem: The All-Pairs Shortest-Paths problem for a graph G=( V,E ) with (possibly negative) edge weights can be solved in O ( |V | 3 log |V | ) time. PS There is a different algorithm – the Floyd-Warshall algorithm – that is also based on dynamic programming, but that runs in O( |V | 3 ) time. shortest path from v i to v k only using v 1 to v m on the way blackboard shortest path from v i to v j only using v 1 to v m-1 v m v k v i shortest path from v j to v k only using v 1 to v m-1 17
TU/e Algorithms (2IL15) – Lecture 6 An alternative approach: Johnson’s algorithm Suppose we want to solve a certain graph problem we have an algorithm ALG that only works for certain types of graphs we want to develop an algorithm for another type of graph Possible approaches A. try to adapt ALG B. try to modify the input graph G into a different graph G such that i. ALG can be applied to G ii. we can easily compute the solution for G from the solution for G 18
Recommend
More recommend