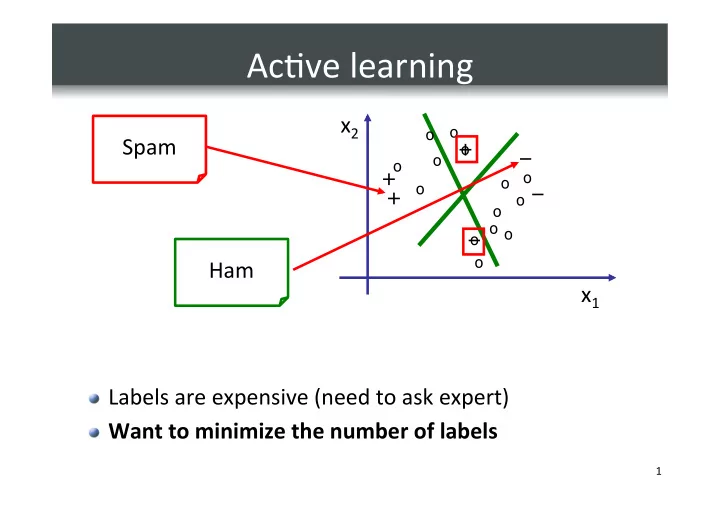
Ac%ve learning x 2 o o Spam + o o o + o o o + - PowerPoint PPT Presentation

Ac%ve ¡learning ¡ x 2 ¡ o o Spam ¡ + o – o o + o o o – + o o o o – o o Ham ¡ x 1 ¡ � Labels ¡are ¡expensive ¡(need ¡to ¡ask ¡expert) ¡ � Want ¡to ¡minimize ¡the ¡number ¡of ¡labels ¡ 1 ¡

Why ¡should ¡ac%ve ¡learning ¡help? ¡ � Example : ¡Learning ¡linear ¡separators ¡in ¡1D ¡ � For ¡now, ¡assume ¡data ¡is ¡noise ¡free ¡ 2 ¡

Does ¡ac%ve ¡learning ¡always ¡help? ¡ 3 ¡

Pool-­‑based ¡ac%ve ¡learning ¡ � Pool-­‑based ¡ac%ve ¡learning ¡ � Obtain ¡large ¡pool ¡of ¡unlabeled ¡data ¡ � Selec%vely ¡request ¡a ¡few ¡labels, ¡un%l ¡we ¡can ¡infer ¡all ¡ remaining ¡labels ¡ � Resul%ng ¡classifier ¡“as ¡good” ¡as ¡that ¡obtained ¡from ¡ complete ¡labeled ¡set ¡ � Reduc%on ¡in ¡labels ¡ � In ¡some ¡cases, ¡exponen%al ¡reduc%on ¡possible! ¡ � In ¡other ¡cases, ¡may ¡need ¡to ¡request ¡almost ¡all ¡labels ¡ � How ¡should ¡we ¡request ¡labels?? ¡ 4 ¡

Uncertainty ¡sampling ¡ � Given ¡pool ¡of ¡ n ¡unlabeled ¡examples ¡ � Repeat ¡un%l ¡we ¡can ¡infer ¡all ¡remaining ¡labels: ¡ � Assign ¡each ¡unlabeled ¡data ¡an ¡ “ uncertainty ¡score ” ¡ � Greedily ¡pick ¡the ¡most ¡uncertain ¡example ¡and ¡request ¡label ¡ � One ¡of ¡the ¡most ¡popular ¡heuris%cs! ¡ 5 ¡

Uncertainty ¡sampling ¡in ¡SVMs ¡ Select ¡point ¡nearest ¡to ¡ hyperplane ¡decision ¡boundary ¡ ? ¡ for ¡labeling ¡ ¡ ¡ w ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ [Tong ¡& ¡Koller, ¡2000; ¡Schohn ¡& ¡Cohn, ¡ 2000; ¡Campbell ¡et ¡al. ¡2000] ¡ 6 ¡

Example: ¡linear ¡classifiers ¡in ¡1D ¡ 7 ¡

Real ¡data ¡example ¡ [Grauman ¡et ¡al] ¡ 8 ¡

Ac%ve ¡learning ¡results ¡ [Grauman ¡et ¡al] ¡ 9 ¡

Uncertainty ¡sampling ¡in ¡large ¡data ¡ � For ¡i ¡= ¡1:max_labels ¡ � For ¡j ¡= ¡1:n ¡ � Calculate ¡uncertainty ¡U(j) ¡score ¡of ¡example ¡j ¡ � Pick ¡most ¡uncertain ¡example ¡ � Retrain ¡SVM ¡ � Complexity ¡to ¡pick ¡m ¡labels? ¡ 10 ¡

Sub-­‑linear ¡%me ¡ac%ve ¡learning ¡ Goal : Map hyperplane query directly to its nearest points. h ( w ) { x , … x } → 1 k ( t ) x 2 ( t ) x 1 ( t 1 ) x + 1 ( t 1 ) x + ( t ) ( t 1 ) x w + ( + t 1 ) 3 w 2 11 ¡ [Jain, Vijayanarasimhan & Grauman, NIPS 2010]

Sub-­‑linear ¡%me ¡ac%ve ¡selec%on ¡ [Grauman ¡et ¡al] ¡ Current ¡Category ¡ Model ¡ Hash ¡func%on ¡ Labeled ¡ Unlabeled ¡ 110.. ¡ data ¡ data ¡ 101.. ¡ Hash ¡func%on ¡ Selected ¡ 111.. ¡ examples ¡ Hashtable ¡ 12 ¡

Hashing ¡a ¡hyperplane ¡query ¡ To ¡retrieve ¡those ¡points ¡for ¡which ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡is ¡small, ¡want ¡ probable ¡collision ¡for ¡ perpendicular ¡vectors: ¡ x 1 Most ¡likely ¡to ¡collide ¡ w Assuming ¡normalized ¡data. ¡ Unlikely ¡to ¡collide ¡ 13 ¡ [Jain, ¡Vijayanarasimhan ¡& ¡Grauman, ¡NIPS ¡2010] ¡

Hashing ¡a ¡hyperplane ¡query ¡ [Grauman ¡et ¡al] ¡ Less ¡likely ¡to ¡split ¡ + ¡Highly ¡likely ¡to ¡split ¡ Less ¡likely ¡to ¡split ¡ + ¡Less ¡likely ¡to ¡split ¡ = ¡Unlikely ¡to ¡collide ¡ = ¡More ¡likely ¡to ¡collide ¡ • Use ¡two ¡random ¡vectors, ¡two-­‑bit ¡hash ¡key ¡ – one ¡to ¡constrain ¡the ¡angle ¡with ¡w ¡ – one ¡to ¡constrain ¡the ¡angle ¡with ¡-­‑w ¡ 14 ¡

Hashing ¡a ¡hyperplane ¡query ¡ [Grauman ¡et ¡al] ¡ Less ¡likely ¡to ¡split ¡ + ¡Highly ¡likely ¡to ¡split ¡ Less ¡likely ¡to ¡split ¡ + ¡Less ¡likely ¡to ¡split ¡ = ¡Unlikely ¡to ¡collide ¡ = ¡More ¡likely ¡to ¡collide ¡ • Use ¡two ¡random ¡vectors, ¡two-­‑bit ¡hash ¡key ¡ – one ¡to ¡constrain ¡the ¡angle ¡with ¡w ¡ – one ¡to ¡constrain ¡the ¡angle ¡with ¡-­‑w ¡ 15 ¡

Hashing a hyperplane query [Grauman ¡et ¡al] ¡ Resulting asymmetric two-bit hash: Let: , ¡

Hashing a hyperplane query [Grauman ¡et ¡al] ¡ Resulting asymmetric two-bit hash: Let: Define hash family: Can calculate LSH collision probability [Jain, Vijayanarasimhan & Grauman, NIPS 2010].

Data flow: Hashing a hyperplane query [Grauman ¡et ¡al] ¡ � Hash all unlabeled data into table � Active selection loop: � Hash current hyperplane as query � Retrieve unlabeled data points with which it collides � Request labels for them � Update hyperplane

Results: ¡Hashing ¡a ¡ hyperplane ¡query ¡ [Grauman ¡et ¡al] ¡ ts ¡as ¡ led ¡ By ¡minimizing ¡ both ¡ selec%on ¡and ¡ labeling ¡%me, ¡provide ¡the ¡best ¡ accuracy ¡per ¡unit ¡%me. ¡ ¡ Tiny ¡Images ¡Dataset ¡/ ¡CIFAR ¡

Results: ¡Hashing ¡a ¡hyperplane ¡query ¡ [Grauman ¡et ¡al] ¡ Learning ¡ Learning ¡ “airplane” ¡ “automobile” ¡ Selected ¡for ¡labeling ¡in ¡ first ¡9 ¡itera%ons ¡ Efficient ¡ac%ve ¡selec%on ¡with ¡pool ¡of ¡1 ¡Million ¡ unlabeled ¡examples ¡and ¡1000s ¡of ¡categories. ¡ ¡

Summary ¡so ¡far: ¡ � Uncertainty ¡sampling: ¡Simple ¡heuris%c ¡for ¡ac%ve ¡ learning ¡ � For ¡SVMs: ¡ ¡ � pick ¡points ¡closest ¡to ¡decision ¡boundary ¡ � Can ¡select ¡efficiently ¡using ¡LSH ¡ � Can ¡get ¡significant ¡gains ¡in ¡labeling ¡cost, ¡even ¡for ¡ large ¡data ¡sets. ¡ � Now: ¡ ¡ � Theory ¡of ¡ac%ve ¡learning ¡ � Criteria ¡beyond ¡uncertainty ¡sampling ¡ 21 ¡

Issues ¡with ¡uncertainty ¡sampling ¡ uncertain ¡≠ ¡informa%ve! ¡ 22 ¡

Defining ¡“informa%veness” ¡ � Need ¡to ¡capture ¡how ¡much ¡“informa%on” ¡we ¡gain ¡about ¡ the ¡true ¡classifier ¡for ¡each ¡label ¡ � Version ¡space: ¡ ¡ set ¡of ¡all ¡classifiers ¡consistent ¡with ¡the ¡data ¡ V ( D ) = { w : ∀ ( x , y ) ∈ D sign( w T x ) = y } � Idea : ¡ ¡ would ¡like ¡to ¡shrink ¡version ¡space ¡as ¡quickly ¡as ¡possible ¡ 23 ¡

Version ¡space ¡for ¡SVM ¡ [Tong ¡& ¡Koller] ¡ 24 ¡

Version ¡space ¡for ¡SVM ¡ [Tong ¡& ¡Koller] ¡ 25 ¡

Version ¡space ¡for ¡SVM ¡ [Tong ¡& ¡Koller] ¡ 26 ¡

Version ¡space ¡for ¡SVM ¡ [Tong ¡& ¡Koller] ¡ 27 ¡

Understanding ¡uncertainty ¡sampling ¡ b ¡ a ¡ c ¡ . ¡ w ¡ e ¡ f ¡ g ¡ d ¡ � Uncertainty ¡sampling ¡picks ¡data ¡point ¡closest ¡to ¡ current ¡solu%on ¡ 28 ¡

Approxima%on ¡for ¡sample ¡selec%on ¡ e ¡ f ¡ . ¡ w ¡ g ¡ � Uncertainty ¡sampling ¡picks ¡data ¡point ¡closest ¡to ¡ current ¡solu%on ¡ 29 ¡

Version ¡space ¡reduc%on ¡ � Ideally : ¡Wish ¡to ¡select ¡example ¡that ¡splits ¡the ¡version ¡ space ¡as ¡equally ¡as ¡possible ¡ � In ¡general, ¡halving ¡may ¡not ¡be ¡possible ¡ ¡ è ¡find ¡“balanced” ¡split ¡ � How ¡do ¡we ¡quan%fy ¡how ¡“balanced” ¡a ¡split ¡is? ¡ e ¡ f ¡ . ¡ w ¡ g ¡ 30 ¡

Relevant ¡version ¡space ¡ � Version ¡space ¡for ¡data ¡set ¡ ¡ D = { ( x 1 , y 1 ) , . . . , ( x k , y k ) } V ( D ) = { w : ∀ ( x , y ) ∈ D sign( w T x ) = y } � Suppose ¡we’re ¡also ¡given ¡an ¡unlabeled ¡pool ¡ ¡ U = { x 0 1 , . . . , x 0 n } � Relevant ¡version ¡space: ¡ ¡ Labelings ¡of ¡pool ¡ consistent ¡with ¡the ¡data ¡ b V ( D ; U ) = { h : U → { +1 , − 1 } : ∃ w ∈ V ( D ) ∀ x ∈ U sign( w T x ) = h ( y ) } 31 ¡