a r = v b c 1 Dot product (scalar - PDF document

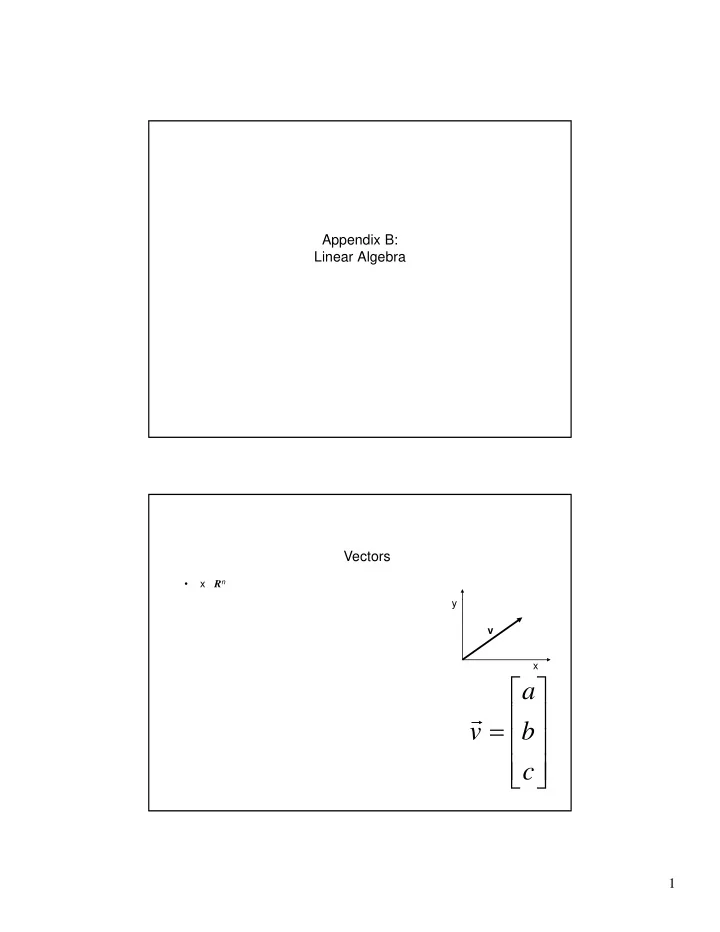
Appendix B: Linear Algebra Vectors • x R n y v x ⎡ a ⎤ ⎢ ⎢ ⎥ ⎥ r = v b ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ c 1

Dot product (scalar product) A B C C B A Cross product • Vector product (cross product) 2

Differentiation of Vectors Linear Independence 3

What is a Matrix? • A matrix is a set of elements, organized into rows and columns g rows ⎡ ⎤ a b ⎢ ⎢ ⎥ ⎥ columns ⎣ ⎦ c d Basic Operations • Addition, Subtraction, Multiplication 4

Multiplication • Is AB = BA? Maybe, but maybe not! • Heads up: multiplication is NOT commutative! p p Matrix Transpose 5

Inverse of a Matrix • Identity matrix: AI = A ⎡ ⎤ 1 0 0 ⎢ ⎥ = I 0 1 0 ⎢ ⎥ ⎢ ⎢ ⎥ ⎥ ⎣ ⎦ 0 0 1 Determinant of a Matrix • Used for inversion ⎡ ⎡ ⎤ ⎤ a b b • If det(A) = 0, then A has no inverse = A ⎢ ⎥ ⎣ ⎦ c d 6

Determinant of a Matrix a b b c = + + − − − d e f aei bfg cdh afh bdi ceg g h i a b c a b c a b c d d e e f f d d e e f f d d e e f f g h i g h i g h i Inverse of a Matrix ⎡ ⎤ a b c 1 0 0 ⎢ ⎢ ⎥ ⎥ + 0 1 0 d e f ⎢ ⎥ ⎢ ⎥ ⎣ g h i 0 0 1 ⎦ 7

Null Space 8