| | | 4 x i 1 x i +1 x i large seeds small seeds - PowerPoint PPT Presentation

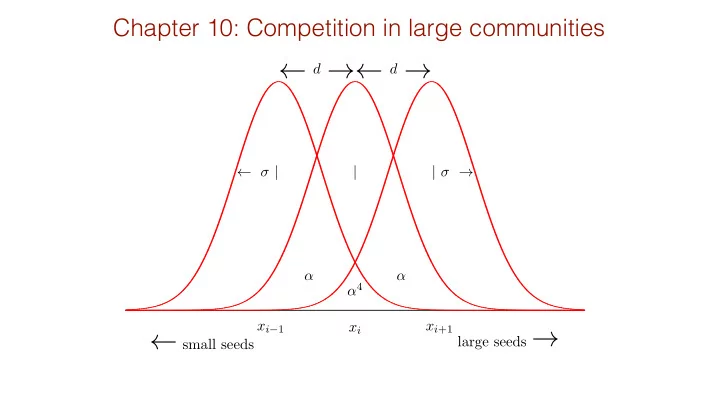
Chapter 10: Competition in large communities ← d d → ← → ← σ | | | σ → α α α 4 x i − 1 x i +1 x i large seeds → ← small seeds

Niche space model 2 σ 2 × e − [ x − d ]2 −∞ e − x 2 R ∞ d x 2 σ 2 2 2 e − ( 2 d 2 σ ) = e − 4 ( d 2 σ ) 2 = e − ( d 2 σ ) = α 4 α = hence −∞ e − x 2 2 σ 2 × e − x 2 R ∞ 2 σ 2 d x α 4 α 9 α 16 0 1 1 . . . α α 4 α 9 1 . . . α α n B C d N i ⇣ ⌘ B C X α 4 α 4 A = 1 . . . d t = rN i 1 − A ij N j with α α B C B C α 9 α 4 α 4 1 . . . j =1 α α @ A . . .

<latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> <latexit sha1_base64="(nul)">(nul)</latexit> n=2, 3, 4, …. d N 1 d N 2 = rN 1 (1 − N 1 − α N 2 ) and = rN 2 (1 − N 2 − α N 1 ) d t d t d N 1 1 rN 1 (1 � N 1 � α N 2 � α 4 N 3 ) , ¯ = N 1 / 3 = d t 1 + α 4 d N 2 = rN 2 (1 � N 2 � α [ N 1 + N 3 ]) , d t d N 3 rN 3 (1 � N 3 � α N 2 � α 4 N 1 ) . = d t d N 2 2 α ' rN 2 (1 � α 2 ¯ 1 + α 4 − 2 α > 0 N ) 1 − 1 + α 4 > 0 or d t

R-script: niche.R model ← function (t, state, parms) { with(as.list(c(state,parms)), { N ← state S ← A %*% N # R code for matrix x vector multiplication dN ← r*N*(1 − S) return (list(dN)) }) } makeMatrix ← function (alpha) { seqAlpha ← sapply(seq(from=0,n − 1), function (i){alpha^(i^2)}) 1.0 A ← matrix(0,nrow=n,ncol=n) ● for (i in seq(n)) { A[i,i:n] ← seqAlpha[1:(n − i+1)] A[i,1:i] ← rev(seqAlpha)[(n − i+1):n] } 0.9 return (A) } findMaxAlpha ← function (n) { n ⇐ n Niche overlap s ← rep(0.1,n) 0.8 names(s) ← paste(" N ",seq(1,n),sep="") for (alpha in seq(0,1,0.01)) { ● A ⇐ makeMatrix(alpha) f ← newton(run(state=s,timeplot= FALSE ),atol=1e − 20) if (min(f) ≡ 0) return (alpha) 0.7 } return (1) } ● ● ● p ← c(r=1) ● 0.6 ● ● n ← 3 s ← rep(0.1,n) ● names(s) ← paste(" N ",seq(1,n),sep="") A ← makeMatrix(0.5) 0.5 f ← newton(run(),atol=1e − 20) nspecies ← seq(9)+1 maxAlpha ← sapply(nspecies,findMaxAlpha) 1 2 2 3 4 4 5 6 6 7 8 8 9 10 10 Number of species size ← 5 #inch pdf(" niche.pdf ",width=size,height=0.75*size) par(mar=c(2.6,2.6,0.2,0.2),mgp=c(1.5,0.5,0)) plot(nspecies,maxAlpha,xlim=c(1,10),ylim=c(0.5,1),xlab=" Number of species ",ylab=" Nich e overlap ") lines(nspecies,maxAlpha) axis(1,at=seq(10,from=0)) dev.off()

Niche space model 1.0 ● 0.9 Niche overlap 0.8 ● 0.7 ● ● ● ● 0.6 ● ● ● 0.5 1 2 2 3 4 4 5 6 6 7 8 8 9 10 10 Number of species

Niche space models: 2-dimensional

Stability and complexity × √   − 1 0 0 0 0 0 a − b . . . 0 − 1 0 0 0 nP < 1 . c . . . σ   J =   0 0 − 1 0 . . .   − 1 − d . . . . . .

maxEigen ← function (n,p,sd) { R-script: gardner.R A ← matrix(0,nrow=n,ncol=n) for (i in seq(n)) for (j in seq(n)) { if (i ≠ j && runif(1) < p) A[i,j] ← rnorm(1,0,sd) } diag(A) ← − 1 return (max(sort(Re(eigen(A)$values)))) } n ← 100 p ← 1 s ← 0.25 maxEigen(n,p,s) s*sqrt(n*p) maxP ← 0.25; nPs ← 10; nTrials ← 20 nstable ← rep(0,nPs) for (i in seq(nPs)) { p ← maxP*i/nPs print(c(P=p,Eq10.11=s*sqrt(n*p))) for (j in seq(nTrials)) nstable[i] ← nstable[i] + ifelse(maxEigen(n,p,s)<0,1,0) } plot(maxP*seq(nPs)/nPs,nstable/nTrials,xlab=" P ",ylab=" Fraction stable ",main=paste(n,s )) curve(s*sqrt(n*p),from=0,to=maxP,xname=" p ",add= TRUE )

Monopolization n m d N a i ⇣ ⌘ X X = N a i 1 − + D ab ( N b i − N a i ) A ij N a j d t j =1 b =1

Stability of food webs From McCann, Nature 1998

Self-assembling food webs From: Law & Blackford, Ecology, 1992