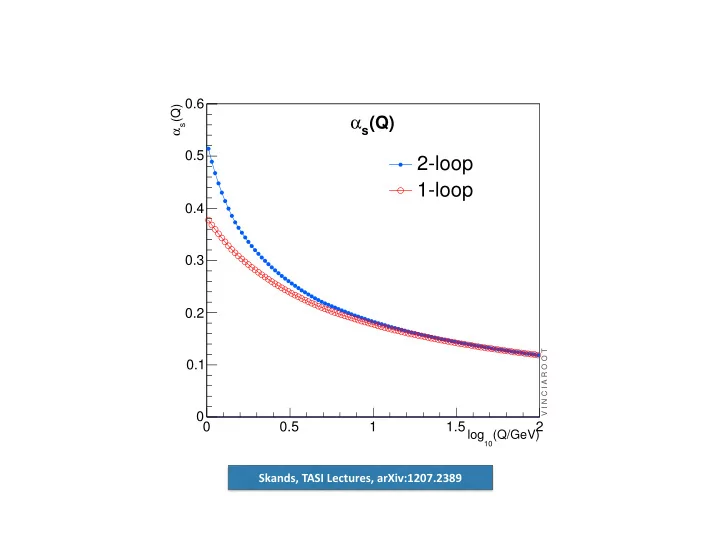

0.6 (Q) (Q) α s s α 0.5 2-loop 1-loop 0.4 0.3 0.2 V I N C I A R O O T 0.1 0 0 0.5 1 1.5 2 log (Q/GeV) 10 Skands, ¡TASI ¡Lectures, ¡arXiv:1207.2389
Hartgring, ¡Laenen, ¡Skands, ¡arXiv:1303.4974 Z → 3 Jets i r y ij = s ij e w o h s M 2 Z Size of NLO “K” factor j y jk = s jk shower over phase space M 2 Z k Q E = 2 p T H strong L Q E = 2 p T H strong L 0 1.75 0 1.5 1.2 1.4 hard hard 1.2 - 2 - 2 1.5 collinear collinear 1.5 ln H y jk L ln H y jk L - 4 - 4 2 1.75 - 6 - 6 soft collinear soft collinear 1.75 1.2 - 8 - 8 - 8 - 6 - 4 - 2 0 - 8 - 6 - 4 - 2 0 ln H y ij L ln H y ij L (a) µ PS = √ s (b) µ PS = p ⊥
Hartgring, ¡Laenen, ¡Skands, ¡arXiv:1303.4974 Z → 3 Jets Size of NLO “K” factor over phase space The “CMW” factor : Constant shift by 8 1 . 513 n F = 6 > α s β 0 > ✓ 67 − 3 π 2 − 10 n F / 3 > ◆ 1 . 569 n F = 5 < k 2 � � 2 ln ∼ 0 . 07 k CMW = exp = CMW 2(33 − 2 n F ) 1 . 618 n F = 4 2 π > > > 1 . 661 n F = 3 Catani, ¡Marchesini, ¡Webber, ¡NPB349 ¡(1991) ¡635 : Q E = 2 p T H strong L Q E = 2 p T H strong L 0 0 1.2 1.2 1.2 1.2 1.1 1.2 - 2 - 2 1.1 1.2 ln H y jk L ln H y jk L - 4 - 4 1.05 - 6 - 6 soft soft 1.2 1.1 - 8 - 8 - 8 - 6 - 4 - 2 0 - 8 - 6 - 4 - 2 0 ln H y ij L ln H y ij L µ PS = p ⊥ , with CMW (b) µ PS = p ⊥
0.8 (Q) α s (2) (MZ)=0.12 (incl var) α s 0.6 (2) (MZ)=0.12 (CMW) α s (1) (MZ)=0.14 α s 0.4 Beware : choosing a larger central scale → a seemingly smaller scale variation! 0.2 V I N C I A R O O T 0 1.2 1.1 Ratio 1 0.9 0.8 0 1 2 3 4 Log10( ) [GeV] µ 2 Loop: α s (M Z )=0.12 Λ 3 = 0.37 Λ 4 = 0.32 Λ 5 = 0.23 1 Loop: α s (M Z )=0.14 Λ 3 = 0.37 Λ 4 = 0.33 Λ 5 = 0.26 (In all cases, 5-flavor running is still used above mt)
Variations in e + e - μ R by factor 2 in either direction Pythia 6 “Perugia 2012 : Variations” (with central choice μ R =p T , and α s (M Z ) (1) ~ 0.14) Skands, ¡ ¡arXiv:1005.3457 Thrust 3j 4j Durham kT Durham kT y 23 y 56 1-T 6-jet observable Event Shape 3-jet observable ∝ α s1 ∝ α s4 → Factor 2 looks Beware! α s pileup pretty extreme? See mcplots.cern.ch Karneyeu ¡et ¡al, ¡ ¡arXiv:1306.3436
Variations in pp μ R by factor 2 in either direction Pythia 6 “Perugia 2012 : Variations” (with central choice μ R =p T , and α s (M Z ) (1) ~ 0.14) Skands, ¡ ¡arXiv:1005.3457 Z W Jets Jet p TZ p Tjet Shape d σ /dp T 1/ σ d σ /dp T → Factor 2 looks “dimensionful” “normalized” See mcplots.cern.ch reasonable? Karneyeu ¡et ¡al, ¡ ¡arXiv:1306.3436
Cooper ¡et ¡al., ¡ ¡arXiv:1109.5295 Matrix Elements W+jets (E.g., AlpGen/MadGraph + Herwig/Pythia) jets) [pb] 4 10 pp, 7 TeV, W+jets, el-chan. P2011 PS , Alp. Λ ↑ Λ ↑ Λ PS ↓ , Λ Alp. ↓ jet Alp. Λ ↑ N Λ Alp. ↓ ≥ (W + 3 10 σ mcplots.cern.ch 2 10 Alpgen+Pythia jet multiplicity 0 1 2 3 N jet Ratio to 1.5 1 0.5 0 1 2 3 Jet Shape � Jet Shape � NJets PS ME+PS NJets: dominated by ME (+Sudakov from PS) Jet Shapes: dominated by PS
From multi-leg LO to multi-leg NLO Hartgring, ¡Laenen, ¡Skands, ¡arXiv:1303.4974 ee hadrons → 91.2 GeV /d(1-T) 1-Thrust (udsc) 4 10 σ 2 /N d χ L3 bins 3 σ 10 5% 1/ (2) 0.5 0.0 ± (MZ)=0.12 (NLO3,CMW) α S 2 10 (1) 0.5 0.1 ± (MZ)=0.14 (LO3) α S 10 (2) 1.4 0.1 ± (MZ)=0.12 (LO3,CMW) α S (2) 15.0 0.6 ± (MZ)=0.12 (LO3) α 1 S -1 10 V I N C I A R O O T -2 10 Data from Phys.Rept. 399 (2004) 71 Vincia 1.104 + MadGraph 4.4.26 + Pythia 8.186 -3 10 1.2 Theory/Data 1.1 1 0.9 0.8 0 0.1 0.2 0.3 0.4 0.5 1-T (udsc)
Multi-scale problems 0.005 W + 3 jets (100, 200, 300) 3 α s E.g., in context of ME 0.004 pT1 = 100 matching with many legs pT2 = 200 0.003 pT3 = 300 1 0.002 4 5 Example: W+3 3 0.001 V I N C I A R O O T 2 0.01 0 W + 3 jets (20, 30, 60) 2 3 α s 0.008 1.5 Ratio pT1 = 20 1 pT2 = 30 0.006 0.5 1 2 3 4 5 pT3 = 60 Central Choice 0.004 4 5 0.003 1 W' + 3 jets (100, 200, 300) 3 800 0.002 V I N C I A R O O T 2 3 α 0.0025 s mW = 800 0 pT1 = 100 0.002 2 pT2 = 200 4 1.5 5 0.0015 Ratio pT3 = 300 1 0.001 1 3 0.5 2 1 2 3 4 5 V I N C I A R O O T Central Choice 0.0005 1: MW � 0 2 2: MW + Sum(|pT|) � 3: -“- (quadratically) � 1.5 Ratio 4: Geometric mean pT (~PS) � 1 5: Arithmetic mean pT 0.5 1 2 3 4 5 Central Choice
Recommend
More recommend