Loop Optimizations Important because lots of execution Loop - PDF document

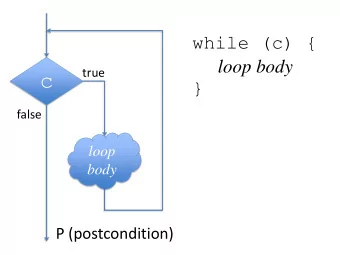
Loop Optimizations ♦ Important because lots of execution Loop Optimizations Loop Optimizations time occurs in loops ♦ First, we will identify loops ♦ We will study three optimizations ♦ Loop-invariant code motion This lecture is primarily based on Konstantinos Sagonas set of slides (Adva Advanced ed Compil Compiler er Techn Techniques es , (2AD518) ♦ Strength reduction at Uppsala University, January-February 2004) . Used with kind permission. ♦ Induction variable elimination Advanced Compiler Techniques 27.04.04 2 http://lamp.epfl.ch/teaching/advancedCompiler/ What is a Loop? Anomalous Situations ♦ Set of nodes ♦ Two back Loop Optimizations Loop Optimizations edges, two ♦ Loop header loops, one header ♦ Single node ♦ Compiler ♦ All iterations of merges loops loop go through header ♦ No loop header, ♦ Back edge no loop Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 3 4 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ Defining Loops With Identifying Loops Dominators Recall the concept of dominators: Loop Optimizations: Identifying loops Loop Optimizations: Dominators ♦ Node n dominates a node m if all paths from the ♦ A loop has a unique entry point – the header. start node to m go through n. ♦ At least one path back to header. ♦ The immediate dominator of m is the last dominator ♦ Find edges whose heads (>) dominate tails (-), of m on any path from start node. these edges are back edges of loops. ♦ A dominator tree is a tree rooted at the start node: ♦ Given a back edge n → d: ♦ Nodes are nodes of control flow graph. ♦ The node d is the loop header. ♦ Edge from d to n if d is the immediate dominator of n. ♦ The loop consists of n plus all nodes that can reach n without going through d (all nodes “between” d and n) Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 5 6 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ 1

Loop Construction Algorithm Nested Loops Loop Optimizations: Identifying loops Loop Optimizations: Identifying loops ♦ If two loops do not have same header then loop (d,n) loop = ∅ ; stack = ∅ ; insert (n); ♦ Either one loop (inner loop) is contained in the other (outer loop) while stack not empty do ♦ Or the two loops are disjoint m = pop stack; ♦ If two loops have same header, typically they for all p ∈ pred (m) do insert (p); are unioned and treated as one loop insert (m) if m ∉ loop then 1 Two loops: loop = loop ∪ {m}; {1,2} and {1, 3} push m onto stack; 2 3 Unioned: {1,2,3} Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 7 8 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ Loop Preheader Loop Optimizations Loop Optimizations: Loop invariant code motion Loop Optimizations: Preheader ♦ Now that we have the loop, we can ♦ Many optimizations stick code before loop. ♦ Put a special node (loop preheader) before optimize it! loop to hold this code. ♦ Loop invariant code motion: ♦ Move loop invariant code to the header. Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 9 10 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ Detecting Loop Invariant Loop Invariant Code Motion Code Loop Optimizations: Loop invariant code motion Loop Optimizations: Loop invariant code motion ♦ A statement is loop-invariant if operands are If a computation produces the same value in every loop iteration, move it out of the loop. ♦ Constant, ♦ Have all reaching definitions outside loop, or t1 = 100*N ♦ Have exactly one reaching definition, and that for i = 1 to N for i = 1 to N x = x + 1 definition comes from an invariant statement x = x + 1 for j = 1 to N ♦ Concept of exit node of loop t2 = t1 + 10*i + x a[i,j] = 100*N + 10*i + j + x for j = 1 to N ♦ node with successors outside loop a[i,j] = t2 + j Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 11 12 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ 2

Loop Invariant Code Loop Invariant Code Motion Detection Algorithm Loop Optimizations: Loop invariant code motion Loop Optimizations: Loop invariant code motion for all statements in loop if operands are constant or have all reaching definitions ♦ Conditions for moving a statement s: x = y+z outside loop, mark statement as invariant into loop header: do ♦ s dominates all exit nodes of loop for all statements in loop not already marked invariant ♦ If it does not, some use after loop might get wrong value ♦ Alternate condition: definition of x from s reaches no use if operands are constant, have all reaching definitions outside loop (but moving s may increase run time) outside loop, or have exactly one reaching definition from ♦ No other statement in loop assigns to x invariant statement ♦ If one does, assignments might get reordered then mark statement as invariant ♦ No use of x in loop is reached by definition other until there are no more invariant statements than s ♦ If one is, movement may change value read by use Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 13 14 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ Order of Statements in Induction Variables Preheader Loop Optimizations: Loop invariant code motion Preserve data dependences from original program Loop Optimizations: Induction Variables (can use order in which discovered by algorithm) Example: b = 2 b = 2 for j = 1 to 100 i = 0 i = 0 *(&A + 4*j) = 202 - 2*j a = b * b i < 80 Basic Induction variable: c = a + a J = 1, 2, 3, 4, ….. a = b * b i < 80 Induction variable &A+4*j: c = a + a &A+4*j = &A+4, &A+8, &A+12, &A+16, …. i = i + c i = i + c Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 15 16 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ What are induction variables? Types of Induction Variables Loop Optimizations: Induction Variables Loop Optimizations: Induction Variables ♦ x is an induction variable of a loop L if ♦ Base induction variable: ♦ Only assignments in loop are of form i = i ± c ♦ variable changes its value every iteration of the loop ♦ Derived induction variables: ♦ the value is a function of number of iterations of ♦ Value is a linear function of a base induction the loop variable. ♦ Within loop, j = c*i + d, where i is a base induction ♦ In programs, this function is normally a linear variable. function ♦ Very common in array index expressions – an access to a[i] produces code like p = a + 4*i. Example: for loop index variable j, function d + c*j Advanced Compiler Techniques 27.04.04 Advanced Compiler Techniques 27.04.04 17 18 http://lamp.epfl.ch/teaching/advancedCompiler/ http://lamp.epfl.ch/teaching/advancedCompiler/ 3