1
play

1 1000 0000 0100 0000 Fast multiplication Division hardware - PDF document

Nov 11, 2022 •463 likes •533 views

0000 1000 Multiplication hardware 0001 0000 0010 0000 Computer arithmetic o The multiplication 0100 0000 algorithm we learned in Multiplicand grammar school leads to 1001 Integers and floats Shift left a simple if somewhat 0100 64 bits

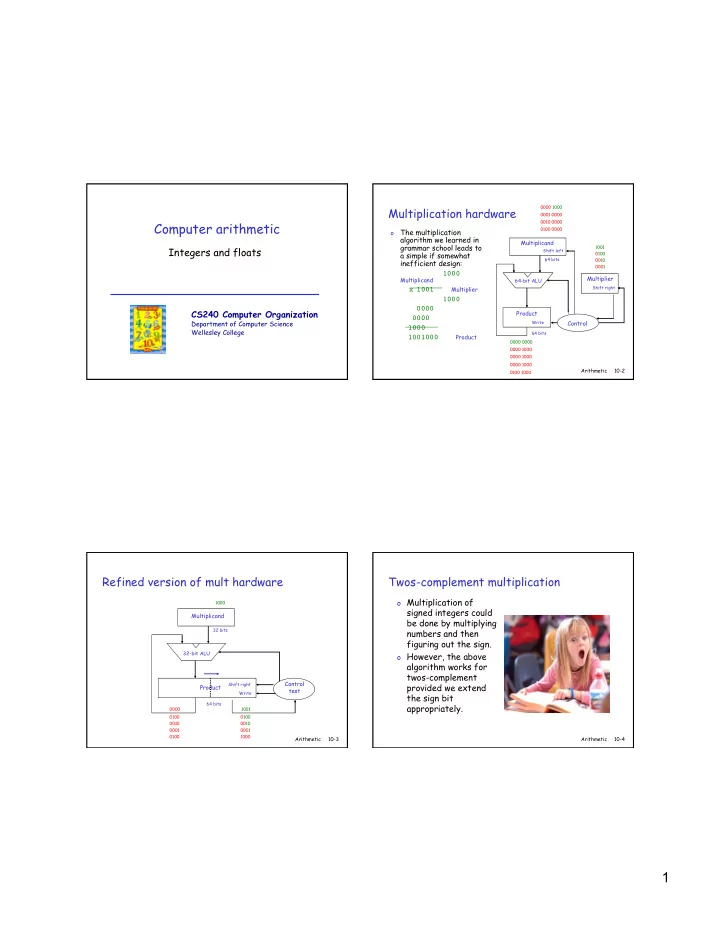
  1. 0000 1000 Multiplication hardware 0001 0000 0010 0000 Computer arithmetic o The multiplication 0100 0000 algorithm we learned in Multiplicand grammar school leads to 1001 Integers and floats Shift left a simple if somewhat 0100 64 bits 0010 inefficient design: 0001 � � � 1000 � Multiplier Multiplicand 64-bit ALU Shift right � 1001 � Multiplier � x � � � 1000 � 0000 � CS240 Computer Organization Product 0000 � Write Control Department of Computer Science 1000 � Wellesley College 64 bits 1001000 Product 0000 0000 � 0000 1000 0000 1000 0000 1000 Arithmetic 10-2 0100 1000 Refined version of mult hardware Twos-complement multiplication o Multiplication of 1000 signed integers could Multiplicand be done by multiplying 32 bits numbers and then figuring out the sign. 32-bit ALU o However, the above algorithm works for twos-complement Control Shift right provided we extend Product test Write the sign bit 64 bits appropriately. 0000 1001 0100 0100 0010 0010 0001 0001 0100 1000 Arithmetic 10-3 Arithmetic 10-4 1

  2. 1000 0000 0100 0000 Fast multiplication Division hardware 0010 0000 0*1000 1*1000 0001 0000 Mplier0 * Mcand 0000 1000 Mplier1 * Mcand 0100 0000 0000 0 Divisor 32-bit ALU 0001 0*1000 Shift right 0010 � 1001 Quotient Mplier2 * Mcand 0010 0100 64 bits 1000 1001010 Dividend 1001 0 32-bit ALU - 1000 � 1*1000 Quotient 64-bit ALU 10 � Mplier3 * Mcand 0001 Shift left 101 � 0 32-bit ALU 1010 � . . . Remainder 0100 - 1000 � 10 Remainder 1 Write Control Mplier31 * Mcand � 64 bits 0100 1010 32-bit ALU 0100 1010 0000 1010 0000 1010 product bits 31 - 0 product bits 63 - 32 0000 1010 Arithmetic 10-5 0000 0010 Arithmetic 10-6 Refined version of division hardware Representing reals o Numbers with fractions, e.g., 3.14159265… ( π ). Divisor o Very small numbers, e.g., . 32 bits 000000001 = 1.0 x 10 -9 o Very large numbers, e.g., 32-bit ALU 3,155,760,000 = 3.15576 x 10 9 Shift right Control Remainder Shift left test Write 64 bits Arithmetic 10-7 Arithmetic 10-8 2

  3. Binary fractions Life is not also so easy o We can also show binary o What if the fractional part is not an exact power of two? We will need to approximate! numbers in normalized scientific notation using 2 -1 = .1 2 = .5 10 the notation: 2 -2 = .01 2 = .25 10 1.xxxx 2 x 2 yyyy 2 -3 = .001 2 = .125 10 2 - 4 = .0001 2 = .0625 10 o We now call the “ . ” symbol 2 -5 = .00001 2 = .03125 10 the binary point. We also 2 -6 = .000001 2 = .015625 10 call this format “ floating- 2 -7 = .0000001 2 = .0078125 10 point ” because the binary 2 -8 = .00000001 2 = .0039063 10 point is not fixed. 2 -9 = .000000001 2 = .0019531 10 2 -10 = .0000000001 2 = .0009766 10 etc… Then, sum to the degree of precision necessary. For example, o what does .3 10 = ? Arithmetic 10-9 Arithmetic 10-10 Floating-point numbers: IEEE 754 floating-point standard (-1) sign x fraction x 2 exponent o Single precision o A fixed word size means that there is a tradeoff between accuracy and range: 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 � o more bits for fraction gives more precision of fraction exponent � fraction � s � o more bits for exponent increases range of numbers that can 1 bit 8 bits 23 bits be represented. o Double precision 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 � exponent � fraction � s � 1 bit 11 bits 20 bits 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 � fraction continued � 32 bits Arithmetic 10-11 Arithmetic 10-12 3

  4. Water over (and under) the dam Some unpleasant details o Overflow is now the case o Placing the exponent before the fraction simplifies sorting where the positive of floating point numbers using integer comparison exponent is too large to instructions. be represented in the o But, what about negative exponents? They “ look ” big exponent field. because the leading digit is a 1! o But now there is also o Exponent is “ biased ” to make sorting easier. The bias is underflow, i.e., the case where the negative subtracted from the normal, unsigned value, to determine exponent is too large to the real value. Bias = 127 for single precision and 1023 for fit in the exponent field. double precision: In this case, the (–1) sign x (1 + fraction) x 2 exponent – bias fractional part has become so small that it cannot be represented. Arithmetic 10-13 Arithmetic 10-14 So an IEEE engineer walks into a bar ... Aaaahhhh!!! ... and orders 1.00000000001000000082740370999090373516082763671875 root beers. The bartender says, "I'll have to charge extra; that's a root beer float". And the engineer says, "In that case, make it a double." We order a -.75 10 float and make it a double. Arithmetic 10-15 Arithmetic 10-16 4

  5. Floating point multiplication: The infamous Pentium bug (1994) 1.000 x 2 -1 times -1.110 x 2 -2 Add exponent without bias: Round the product: 1. 4. -1 + (-2) = -3 � 1.110 x 2 -3 Multiple significants: Calculate sign of result: 2. 5. 1.000 � 1 x (-1) = -1 � � x 1.110 � � � � 0000 � � � 1000 � � � 1000 � � � 1000 � � 1.110000 � Normalize and check for 3. overflow or underflow: 1.110 x 2 -3 Arithmetic 10-17 Arithmetic 10-18 5

Recommend

More recommend