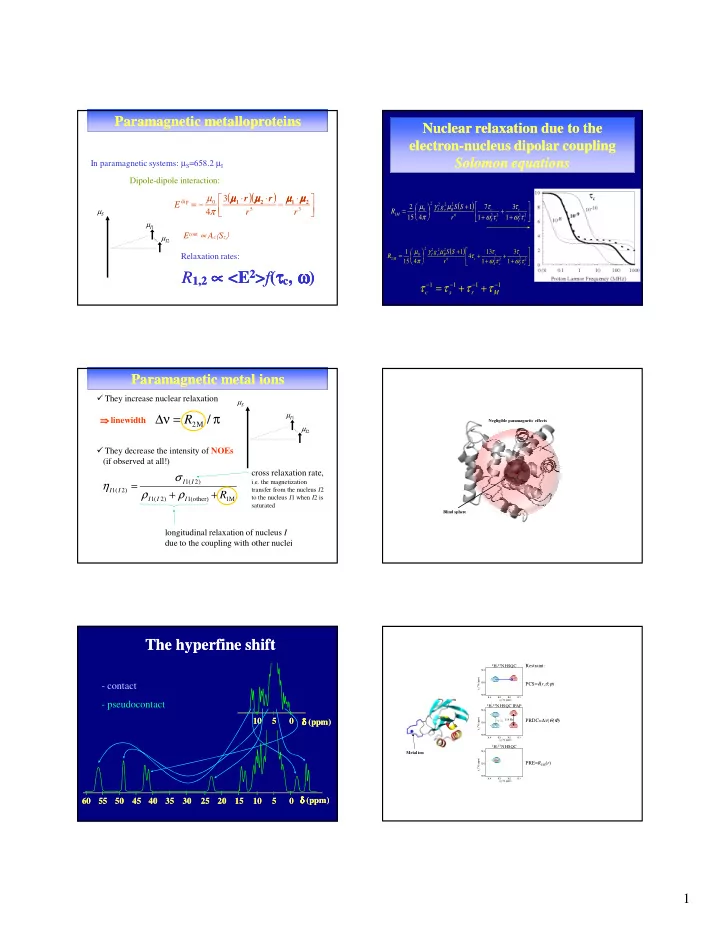
1 2 lt e lt e 2 gt f
play

1,2 <E <E 2 > f ( c , - PDF document

Aug 09, 2023 •584 likes •784 views

Paramagnetic metalloproteins Paramagnetic metalloproteins Nuclear relaxation due to the Nuclear relaxation due to the electron electron-nucleus dipolar coupling nucleus dipolar coupling Solomon equations Solomon equations In paramagnetic

  1. Paramagnetic metalloproteins Paramagnetic metalloproteins Nuclear relaxation due to the Nuclear relaxation due to the electron electron-nucleus dipolar coupling nucleus dipolar coupling Solomon equations Solomon equations In paramagnetic systems: µ S =658.2 µ I Dipole-dipole interaction: τ c � 3 ( )( ) � µ µ µ µ µ ⋅ r µ µ µ µ ⋅ r µ µ µ µ ⋅ µ µ µ µ dip 0 1 2 1 2 E = − − 2 � � � � 2 � � 2 2 2 ( 1 ) 7 3 µ γ µ + τ τ g S S 5 3 4 � � � 0 � π = I e B � c + c � µ S r r R 1 M 15 � 4 � 6 1 2 2 1 2 2 π � + ω τ + ω τ � r S c I c µ I 1 E cont ∝ A c � S z � µ I 2 2 2 2 2 ( ) � � 1 � � 1 13 3 µ γ g µ S S + τ τ Relaxation rates: 0 � � I e B � 4 c c � R = τ + + 2 M 15 � 4 � 6 c 1 2 2 1 2 2 π r � + ω τ + ω τ � S c I c 1,2 ∝ ∝ ∝ ∝ ∝ ∝ ∝ <E ∝ <E 2 > f ( τ τ τ τ τ τ c τ τ , ω ω ω ) ω ω ω ω ω R 1,2 c , 1 1 1 1 − − − − τ = τ + τ + τ c s r M Paramagnetic metal ions Paramagnetic metal ions � They increase nuclear relaxation µ S / µ I 1 ∆ν = π � � � � linewidth R 2 M Negligible paramagnetic effects µ I 2 � They decrease the intensity of NOEs (if observed at all!) cross relaxation rate, σ 1 ( 2 ) i.e. the magnetization I I η = transfer from the nucleus I 2 1 ( 2 ) I I ρ + ρ + R to the nucleus I 1 when I 2 is 1 ( 2 ) 1 (other) 1 M I I I saturated Blind sphere longitudinal relaxation of nucleus I due to the coupling with other nuclei The hyperfine shift The hyperfine shift 1 H- 15 N HSQC Restraint: 124 15 N) (ppm) - contact 126 PCS= δ ( r , ϑ , ϕ ) δ 1 ( 128 8.4 8.3 8.2 8.1 - pseudocontact δ 2 ( 1 H) (ppm) 1 H- 15 N HSQC IPAP 124 10 10 5 0 15 N) (ppm) PRDC= ∆ ν ( Θ , Φ ) δ δ δ δ δ δ δ (ppm) δ (ppm) 94 Hz 114 Hz 126 δ 1 ( 128 8.4 8.3 8.2 8.1 δ 2 ( 1 H) (ppm) 1 H- 15 N HSQC 124 Metal ion 15 N) (ppm) PRE= R 1M ( r ) 126 δ 1 ( 128 8.4 8.3 8.2 8.1 δ 2 ( 1 H) (ppm) 60 60 55 55 50 50 45 45 40 40 35 35 30 30 25 25 20 20 15 15 10 10 5 0 δ (ppm) δ δ δ δ δ δ δ (ppm) 1

  2. Magnetic moments and magnetic fields Magnetic moments and magnetic fields Average magnetic moment Average magnetic moment ∆ E = g µ B = � γ B ∆ E = g e µ B 0 0 0 N N N B g � � I � γ � = γ I = − µ B g S N N I e 1.86 × 10 − 23 JT − 1 1 H 5.59 2.81 × 10 − 26 JT − 1 g µ = e B 0.86 0.43 2 H 5.96 2.99 g µ B g µ g µ 3 H e B 0 e B e B ω = = γ B = ω 13 C 1.40 0.71 S N 0 I B 0 � � � γ γ N N 0.40 0.20 <µ>≠0 14 N <µ>=0 15 N − 0.57 − 0.28 400 MHz 1 H Larmor frequency 31 P 2.26 1.14 = 263 GHz of electron Larmor frequency µ is 658 times larger than µ I B 0 � = − µ B g S e ∆ E = g e µ B m S =±½ 0 B < µ >= − µ < > g S B e z Paramagnetic susceptibility Paramagnetic susceptibility Curie law Curie law Paramagnetic systems: < µ >= − µ < > g S B e z � ( ) , | | , exp / < S M S S M > − E kT , S z S S M B 0 z S z , B 0 S M S < S >= � ( ) z < µ µ µ > µ exp / − E kT , S M � ⋅ S E = B ∆ E = g e µ B , m S =±½ 0 S M B S Zeeman 0 y y E = g µ M B Zeeman energy of the level m S = − 1/2 , 0 x x S M e B S S if no contribution from the orbital magnetic moment χ B 0 P1/P0=exp(- ∆ E/kT) < µ >= 1.86 ·10 -23 ·20/2 <<1.38·10 -23 ·298 If g e µ B B 0 M S << kT µ g µ B 0 0 ( 1 ) e B < S >= − S S + z 3 χ = paramagnetic susceptibility per molecule, kT � B � 0 < > = independent on B 0 and positive � 0 µ < µ > µ 0 2 2 0 ( 1 ) χ = = µ g S S + Curie law: B e 3 B kT 0 Magnetic susceptibility anisotropy Magnetic susceptibility anisotropy Average magnetic moment Average magnetic moment In systems that are orbitally non-degenerate, the anisotropy If the orbital magnetic moment is considered, χ χ is anisotropic χ χ can be represented by an anisotropy of the g -factor χ χ χ χ ⋅ B � ( ) | | 1 / � 0 < φ L + g S φ > − E kT < > = i kk e kk i i kk µ i < µ >= − µ < >= − µ 0 g S � ( ) kk B kk kk B 1 / − E kT i kk B z i g kk µ M B E i kk = 0 < µ µ > is NOT PARALLEL to B 0 | | B S µ µ < φ + φ >= L g S g M B 0 kk e kk kk S Zeeman energy < µ > z < µ > is orientation dependent ( 1 ) + S S 2 2 χ = µ µ g kk 0 kk B 3 < µ µ > µ µ kT Valid with only one thermally populated multiplet of spin number S B x < µ > x NO zero field splitting 2

  3. Van Vleck equation Van Vleck equation The origin of contact shifts The origin of contact shifts if the total energy of the system E 0 >> Zeeman energy Contact shift ontact shift : c : contribution to the ontribution to the E 0 = zero field splitting and ligand field energy chemical shift due to the unpaired chemical shift due to the unpaired � 2 � electron spin electron spin density density on the resonating on the resonating 2 | | | | < φ L + g S φ > � < φ L + g S φ > � � � ( ) i kk e kk j 0 i kk e kk i 2 exp / − − E kT � 0 0 � i kT − nucleus nucleus E E � ≠ � i j i i j 2 χ = µ µ � 0 ( ) kk B 0 exp / − E kT i The coupling constant between nucleus and e - I 1 …e - is called A i � the interaction is expressed by Energies of ground and H = A I ⋅ S excited states A: contact hyperfine contact hyperfine c coupling proportional to the spin oupling proportional to the spin are anisotropic < S >∝< µ >∝ χ density of the resonating nucleus density of the resonating nucleus z Contact shifts Contact shifts Electronic configuration of Electronic configuration of III Heme LS Fe III ( 1 ) LS Fe Heme S S + B 0 < >= − µ S g = A I ⋅ S H z B e 3 kT H.M. McConnell, D.B. Chesnut, J.Chem.Phys. 1958 , 28 , 107-117 N y x φ φ φ φ C N N 3 Fe N N 1 d xz I II - φ φ φ φ θ 3 g xx N d yz π π π π d xy Kurland and McGarvey (1970) predict that < S i > and hence contact N C 2 shift may be orientation dependent due to spin-orbit coupling IV III 8 5 R.J. Kurland, B.R. McGarvey, J.Magn.Reson. 1970 , 2 , 286-301 Contact shift restraints: Contact shift restraints: unpaired electron spin density unpaired electron spin density Calculated vs. observed shifts of methyl Calculated vs. observed shifts of methyl on heme nuclei is a function of axial ligand orientation on heme nuclei is a function of axial ligand orientation protons in histidine protons in histidine-cyanide cytochromes cyanide cytochromes Methyl protons in histidine cytochromes (Low spin Fe(III)) Low spin Fe(III)) 8-CH 3 5-CH 3 1-CH 3 3-CH 3 M80A cyano-cytochrome c N N Fe N y x φ φ φ φ From the fit of the methyl shifts: φ = 57 o ± 9 o 18 . 4 sin 2 ( ) 0 . 8 cos 2 ( ) 6 . 1 δ = θ − φ − θ + φ + i i i 3 Bren, Gray, Banci, Bertini, Turano J.Am.Chem.Soc. (1995) 1 I II - φ φ φ φ θ 49 o 3 g xx φ = Banci, Bertini at al. JBIC (1996) structure π π π π I. Bertini, C. Luchinat, G. Parigi, F.A. Walker, JBIC 1999 III IV 8 5 3

Recommend

More recommend