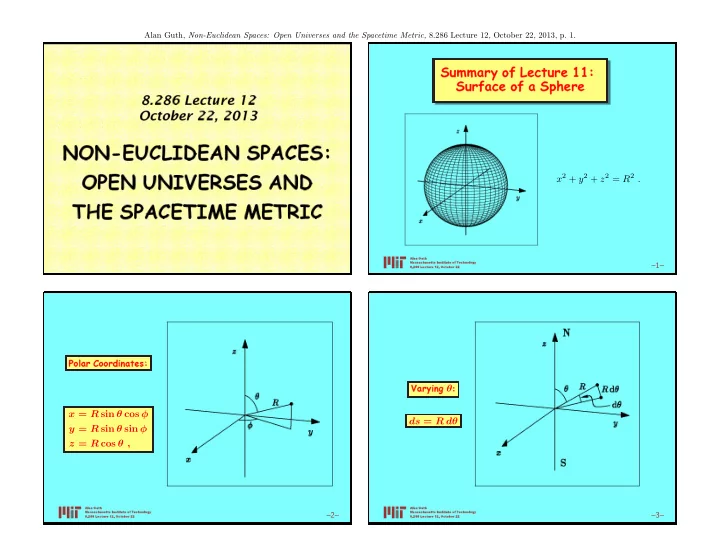
x 2 y 2 z 2 r 2
play

x 2 + y 2 + z 2 = R 2 . OPEN UNIVERSES AND THE SPACETIME METRIC - PowerPoint PPT Presentation

Oct 22, 2022 •24 likes •64 views

Alan Guth, Non-Euclidean Spaces: Open Universes and the Spacetime Metric, 8.286 Lecture 12, October 22, 2013, p. 1. Summary of Leture 11: Surfae of a Sphere 8.286 Leture 12 Otober 22, 2013 NON-EUCLIDEAN SPACES: x 2 + y 2 + z 2 =

  1. Alan Guth, Non-Euclidean Spaces: Open Universes and the Spacetime Metric, 8.286 Lecture 12, October 22, 2013, p. 1. Summary of Le ture 11: Surfa e of a Sphere 8.286 Le ture 12 O tober 22, 2013 NON-EUCLIDEAN SPACES: x 2 + y 2 + z 2 = R 2 . OPEN UNIVERSES AND THE SPACETIME METRIC Alan Guth Massa husetts Institute of T e hnology –1– 8.286 Le ture 12, O tober 22 Polar Coordinates: Varying θ : x = R sin θ cos φ ds = R dθ y = R sin θ sin φ z = R cos θ , Alan Guth Alan Guth Massa husetts Institute of T e hnology Massa husetts Institute of T e hnology –2– –3– 8.286 Le ture 12, O tober 22 8.286 Le ture 12, O tober 22

  2. Alan Guth, Non-Euclidean Spaces: Open Universes and the Spacetime Metric, 8.286 Lecture 12, October 22, 2013, p. 2. Varying θ and φ Varying φ : Varying θ : ds = R dθ Varying φ : ds = R sin θ dφ ds = R sin θ dφ ds 2 = R 2 � dθ 2 + sin 2 θ dφ 2 � Alan Guth Alan Guth Massa husetts Institute of T e hnology Massa husetts Institute of T e hnology –4– –5– 8.286 Le ture 12, O tober 22 8.286 Le ture 12, O tober 22 Review of Le ture 11: A Closed Three-Dimensional Spa e Metri for the Closed 3D Spa e x 2 + y 2 + z 2 + w 2 = R 2 Varying ψ : ds = R dψ x = R sin ψ sin θ cos φ ds 2 = R 2 sin 2 ψ ( dθ 2 + sin 2 θ dφ 2 ) Varying θ or φ : y = R sin ψ sin θ sin φ z = R sin ψ cos θ If the variations are orthogonal to each other, then ds 2 = R 2 � dψ 2 + sin 2 ψ dθ 2 + sin 2 θ dφ 2 �� w = R cos ψ , � ds = R dψ Alan Guth Alan Guth Massa husetts Institute of T e hnology Massa husetts Institute of T e hnology –6– –7– 8.286 Le ture 12, O tober 22 8.286 Le ture 12, O tober 22

  3. Alan Guth, Non-Euclidean Spaces: Open Universes and the Spacetime Metric, 8.286 Lecture 12, October 22, 2013, p. 3. Review of Le ture 11: Impli ations of General Relativity Proof of Orthogonality of Variations ds 2 = R 2 � dψ 2 + sin 2 ψ dθ 2 + sin 2 θ dφ 2 �� � , where R is radius of curvature. � Let dR ψ = displacement of point when ψ is changed to ψ + dψ . According to GR, matter causes space to curve. � Let dR θ = displacement of point when θ is changed to θ + dθ . a 2 ( t ) R cannot be arbitrary. Instead, R 2 ( t ) = . (3) (3) d� d� R ψ · d� R θ = d� d� R θ has no w -component = R ψ · R θ , k ⇒ where (3) denotes the projection into the x - y - z subspace. Finally, � (3) � (3) dR ψ is radial; dR θ is tangential r 2 � d d θ 2 + sin 2 θ d φ 2 �� d s 2 = a 2 ( t ) + r 2 � , dR ψ · � (3) � (3) 1 − kr 2 = dR θ = 0 ⇒ sin ψ where r = √ . Called the Robertson-Walker metric. k Alan Guth Massa husetts Institute of T e hnology –8– –9– 8.286 Le ture 12, O tober 22

  4. MIT OpenCourseWare http://ocw.mit.edu 8.286 The Early Universe Fall 2013 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

Recommend

More recommend