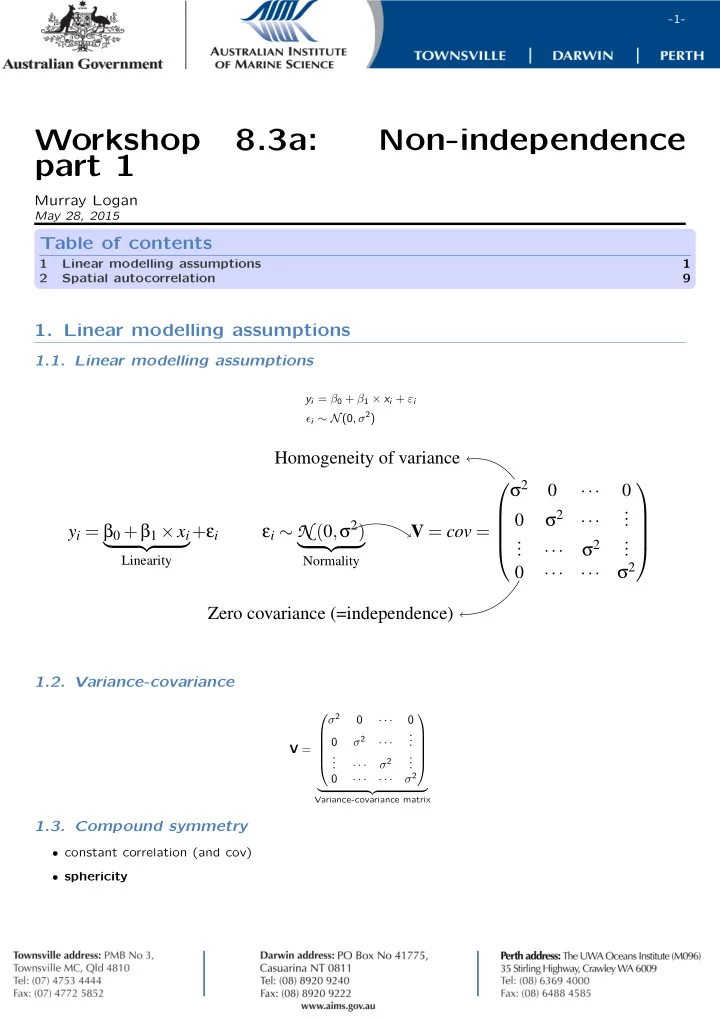
workshop 8 3a non independence part 1
play

Workshop 8.3a: Non-independence part 1 Murray Logan May 28, 2015 - PDF document

Oct 10, 2022 •335 likes •536 views

-1- Workshop 8.3a: Non-independence part 1 Murray Logan May 28, 2015 Table of contents . 1 Linear modelling assumptions 1 2 Spatial autocorrelation 9 1. Linear modelling assumptions 1.1. Linear modelling assumptions y i = 0 + 1

  1. -1- Workshop 8.3a: Non-independence part 1 Murray Logan May 28, 2015 Table of contents . 1 Linear modelling assumptions 1 2 Spatial autocorrelation 9 1. Linear modelling assumptions 1.1. Linear modelling assumptions y i = β 0 + β 1 × x i + ε i ϵ i ∼ N (0, σ 2 ) Homogeneity of variance   σ 2 . 0 0 ··· . .  σ 2  0 . ··· σ 2 )   y i = β 0 + β 1 × x i + ε i ε i ∼ N ( 0 , . V = cov = . . .   . . σ 2 � �� � � �� �  . .  ··· Linearity Normality σ 2 . 0 ··· ··· Zero covariance (=independence) . . . 1.2. Variance-covariance   σ 2 0 · · · 0 .  .  σ 2 · · · . 0   V =   . .   . . σ 2 . · · · .   σ 2 0 · · · · · · � �� � Variance-covariance matrix 1.3. Compound symmetry • constant correlation (and cov) • sphericity

  2. -2-   1 ρ · · · ρ .  .  · · · ρ 1 .   cor ( ε ) =   .   . ... · · · 1 .   ρ · · · · · · 1 � �� � Correlation matrix   θ + σ 2 θ · · · θ .  .  θ + σ 2 θ · · · .   V =   . .   . . θ + σ 2 . · · · .   θ + σ 2 θ · · · · · · � �� � Variance-covariance matrix 1.4. Temporal autocorrelation • correlation dependent on proximity • data.t 0 20 40 60 80 100 30 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 20 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● y ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 10 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 100 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 80 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 60 ● ● ● ● ● ● ● ● ● ● ● ● ● x ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 40 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 20 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 2010 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● 2005 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● year 2000 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● 1995 ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1990 ● ● ● ● ● ● ● ● ● ● 0 10 20 30 1990 1995 2000 2005 2010 1.5. Temporal autocorrelation • Relationship between Y and X > data.t.lm <- lm(y~x, data=data.t) . . > par(mfrow=c(2,3)) > plot(data.t.lm, which=1:6, ask=FALSE)

  3. -3- Residuals vs Fitted Normal Q−Q Scale−Location 96 ● 20 Standardized residuals 6 ● 21 ● ● ● 21 Standardized residuals 2 21 ● 6 ● 6 ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1.2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ●● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● 10 ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1 ● ● ● ● ● ● ● ● ● ● Residuals ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0.8 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0.4 ● ● ● ● ● ● ● ● ● ● ● ● ● ● −1 ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ●● ● ● ● ● ● ● ● ● ● ● ● −20 ● ● ● ● ● ● ● 96 ● ● −2 0.0 ● 96 9.5 10.5 11.5 12.5 −2 −1 0 1 2 9.5 10.5 11.5 12.5 Fitted values Theoretical Quantiles Fitted values Cook's dist vs Leverage h ii ( 1 − Cook's distance Residuals vs Leverage 0.06 2.5 2 1.5 96 96 7 ● 7 ● Standardized residuals 2 ● ● 6 ● ● 7 ● ● ● 6 ● ● 6 ● ● Cook's distance ● Cook's distance ● ● ● ● ● 0.04 ● 1 ● 0.04 ● ● 1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● 0.02 ● 0.02 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0.5 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −2 ● ● ● Cook's distance ● ● ● ● ● ● ● ● ● ● ● 0.00 96 0.00 ●● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● 0 ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● 0 20 40 60 80 100 0.00 0.01 0.02 0.03 0.04 0.01 0.02 0.03 0.04 Leverage h ii Obs. number Leverage 1.6. Temporal autocorrelation • Relationship between Y and X . . > acf(rstandard(data.t.lm))

  4. -4- Series rstandard(data.t.lm) 1.0 0.8 0.6 ACF 0.4 0.2 0.0 −0.2 0 5 10 15 20 Lag 1.7. Temporal autocorrelation • can we partial out time . . > plot(rstandard(data.t.lm)~data.t$year) 2 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 1 ● ● ● ● ● ● ● ● ● ● rstandard(data.t.lm) ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 0 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −1 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● −2 ● 1990 1995 2000 2005 2010 data.t$year

Recommend

Workshop 8.3a: Non-independence part 1 Murray Logan 28 May 2015 Section 1 Linear modelling

Workshop 8.3a: Non-independence part 1 Murray Logan 28 May 2015 Section 1 Linear modelling

Workshop 8.3a: Non-independence part 1 Murray Logan 28 May 2015 Section 1 Linear modelling assumptions Linear modelling assumptions y i = 0 + 1 x i + i i N (0 , 2 ) Homogeneity of variance 2 . 0 0

507 views • 40 slides
::::::i function = O c- zero - - - t en Tn C , et , t = O = eye

::::::i function = O c- zero - - - t en Tn C , et , t = O = eye

Independence of charades of Characters Independence III : ( OPTIONAL ) In depone of of auratus : Part I From ::::::i function = O c- zero - - - t en Tn C , et , t = O = eye Then e , = - - - . NewSt

189 views • 8 slides
Developing independence and good practice - Tips Workshop 1 2 Outline Learning outcomes Brief

Developing independence and good practice - Tips Workshop 1 2 Outline Learning outcomes Brief

1 Developing independence and good practice - Tips Workshop 1 2 Outline Learning outcomes Brief talk covering ideas that will help in the workshop Directory structure, working directories, relative and absolute paths Housekeeping A few

376 views • 13 slides
[ | ] independence Two events E and F are independent if P(EF) = P(E) P(F) equivalently:

[ | ] independence Two events E and F are independent if P(EF) = P(E) P(F) equivalently:

CSE 312, 2011 Winter, W.L.Ruzzo 5. independence [ | ] independence Two events E and F are independent if P(EF) = P(E) P(F) equivalently: P(E|F) = P(E) otherwise, they are called dependent 2 independence Roll two dice, yielding values

533 views • 21 slides
Mentoring and Mentoring Up: Workshop #4: Fostering independence 1. Intro to Mentoring and Mentoring

Mentoring and Mentoring Up: Workshop #4: Fostering independence 1. Intro to Mentoring and Mentoring

3/22/2013 Our workshops on mentoring and mentoring up Mentoring and Mentoring Up: Workshop #4: Fostering independence 1. Intro to Mentoring and Mentoring Up by building trust Maintaining Effective Communication 2. Aligning Goals and

537 views • 5 slides
Epigraphy workshop in Rab Epigraphy workshop in Rab Part I: A second week in Rab Part II:

Epigraphy workshop in Rab Epigraphy workshop in Rab Part I: A second week in Rab Part II:

Epigraphy workshop in Rab Epigraphy workshop in Rab Part I: A second week in Rab Part II: Epigraphy in Rab: preliminary conclusions Part III: Prospects Part I: a second week in Rab More inscriptions -Completing the collection

697 views • 16 slides
Tribunal independence Pamela OConnor Monash University Pam.oconnor@monash.edu Questions about

Tribunal independence Pamela OConnor Monash University Pam.oconnor@monash.edu Questions about

Tribunal independence Pamela OConnor Monash University Pam.oconnor@monash.edu Questions about tribunal independence What is it? Why does it matter? Is it under threat, and from whom? Is it part of judicial independence?

139 views • 12 slides
Categorical data Modelling and Independence R.W. Oldford Eikosograms - Dependence/independence

Categorical data Modelling and Independence R.W. Oldford Eikosograms - Dependence/independence

Categorical data Modelling and Independence R.W. Oldford Eikosograms - Dependence/independence As with continuous data, interest lies in assessing whether the values of Categorical variates might have been generated independently. Independence

835 views • 47 slides
Lecture 3 Conditional Independence CS 886 Sept 21, 2010 Testing Independence Given BN, how

Lecture 3 Conditional Independence CS 886 Sept 21, 2010 Testing Independence Given BN, how

Lecture 3 Conditional Independence CS 886 Sept 21, 2010 Testing Independence Given BN, how do we determine if two variables X, Y are independent (given evidence E)? we use a (simple) graphical property D-separation : A set of

894 views • 6 slides
New QAP Priorities: Veterans Housing and Independence Enabling Housing (IEH) Units 2018

New QAP Priorities: Veterans Housing and Independence Enabling Housing (IEH) Units 2018

New QAP Priorities: Veterans Housing and Independence Enabling Housing (IEH) Units 2018 Application Workshop | January 18, 2018 Jennifer S Schmidt, T Tax C Credit A Administrator New Priorities Independence E Enabling Housi sing

600 views • 10 slides
Judicial Independence Judicial Independence is not a privilege or prerogative of judicial office.

Judicial Independence Judicial Independence is not a privilege or prerogative of judicial office.

Judicial Independence Judicial Independence is not a privilege or prerogative of judicial office. It is the responsibility imposed on each judge to enable him or her to adjudicate a dispute honestly and impartially and without fear of

313 views • 8 slides
Order Independence Krzysztof R. Apt CWI and University of Amsterdam Order Independence p.

Order Independence Krzysztof R. Apt CWI and University of Amsterdam Order Independence p.

Order Independence Krzysztof R. Apt CWI and University of Amsterdam Order Independence p. 1/2 Preliminaries Order Independence p. 2/2 Dominance by a Pure Strategy X Y 2 , 1 , A 1 , 0 , B 2 , 0 , C A

445 views • 23 slides
Revolution grievances against British policies and actions in the Declaration of Independence .

Revolution grievances against British policies and actions in the Declaration of Independence .

NEW YORK STATE STANDARD 7.3 AMERICAN INDEPENDENCE: Growing tensions over political power and economic issues sparked a movement for independence from Great Britain. New York played a critical role in the course and outcome of the The American

1.02k views • 55 slides
3. Independence and Random Variables Andrej Bogdanov Independence of two events Let E 1 be

3. Independence and Random Variables Andrej Bogdanov Independence of two events Let E 1 be

ENGG 2430 / ESTR 2004: Probability and Sta.s.cs Spring 2019 3. Independence and Random Variables Andrej Bogdanov Independence of two events Let E 1 be first coin comes up H E 2 be second coin comes up H Then P ( E 2 | E 1 ) = P (

548 views • 41 slides
ni Txizx ] &quot; Independence, Continued Example: Max of Two Exponentials Min of n Uniforms

ni Txizx ] &quot; Independence, Continued Example: Max of Two Exponentials Min of n Uniforms

Not Too Different From Discrete... A Note on Independence For continuous RVs, what is weird about the Continuous RVs Continued: Discrete RV: following? X and Y are independent iff for all a , b : Independence, Conditioning, P [ X = a , Y = b ]

373 views • 5 slides
Multifaced noncommutative stochastic independence Malte Gerhold University of Greifswald 22 May

Multifaced noncommutative stochastic independence Malte Gerhold University of Greifswald 22 May

Multifaced noncommutative stochastic independence Malte Gerhold University of Greifswald 22 May 2020 ACPMS Trondheim Moeckow Multifaced random variables Moments and cumulants Bi-monotone independence A 4-faced independence More

1.26k views • 87 slides
Independence Deepwater Project INDEPENDENCE HUB CHEYENNE JUBILEE MERGANSER VORTEX Q ATLAS /

Independence Deepwater Project INDEPENDENCE HUB CHEYENNE JUBILEE MERGANSER VORTEX Q ATLAS /

Independence Deepwater Project INDEPENDENCE HUB CHEYENNE JUBILEE MERGANSER VORTEX Q ATLAS / ATLAS NW MONDO SPIDERMAN SAN JACINTO Eastern Planning Area Discoveries within the project were made in 2002 thru 2005 and include blocks bought

497 views • 6 slides
Times of Troubles Ukraine on the Threshold of Independence Independence Attempts March 1917

Times of Troubles Ukraine on the Threshold of Independence Independence Attempts March 1917

Times of Troubles Ukraine on the Threshold of Independence Independence Attempts March 1917 Kiev forms Rada Historian Hrushevsky elected President July 1917 recognized by Russia, UK, France Pro-Bolshevick troops seize Kiev December

552 views • 25 slides
A Divided Nation Only 1/3 of the colonists were in favor of a war for independence: they were

A Divided Nation Only 1/3 of the colonists were in favor of a war for independence: they were

The American 1776- 1783 Revolution Begins A Divided Nation Only 1/3 of the colonists were in favor of a war for independence: they were called Patriots _______________ ! One third were opposed to a war for independence they were

168 views • 5 slides
Quasi-Exact Tests for the dichotomous Rasch Model conditional independence (local

Quasi-Exact Tests for the dichotomous Rasch Model conditional independence (local

Introduction Rasch model Properties unidimensionality/homogenous items Quasi-Exact Tests for the dichotomous Rasch Model conditional independence (local independence) specific objectivity/sample independence Ingrid Koller, Vienna

520 views • 6 slides
Independence and Interoperability in Database Systems Stephen J. Hegner Department of Computing

Independence and Interoperability in Database Systems Stephen J. Hegner Department of Computing

Independence and Interoperability in Database Systems Stephen J. Hegner Department of Computing Science Ume a University Sweden 0 Independence vs. Interoperability Independence: the ability to alter a basic

428 views • 24 slides
Great Northwest Independence Neighborhood Initiative -Group Three- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Three- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Three- A Detailed Action Plan Prepared By: The Community Development Department The City of Independence 111 E. Maple Independence, MO 64050 September, 2007 1 Great Northwest

317 views • 9 slides
Great Northwest Independence Neighborhood Initiative -Group Five- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Five- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Five- A Detailed Action Plan Prepared By: The Community Development Department The City of Independence 111 E. Maple Independence, MO 64050 February 2008 1 Great Northwest

429 views • 9 slides
Great Northwest Independence Neighborhood Initiative -Group Four- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Four- A Detailed Action Plan

Great Northwest Independence Neighborhood Initiative -Group Four- A Detailed Action Plan Prepared By: The Community Development Department The City of Independence 111 E. Maple Independence, MO 64050 November, 2007 1 Great Northwest

375 views • 9 slides

More recommend