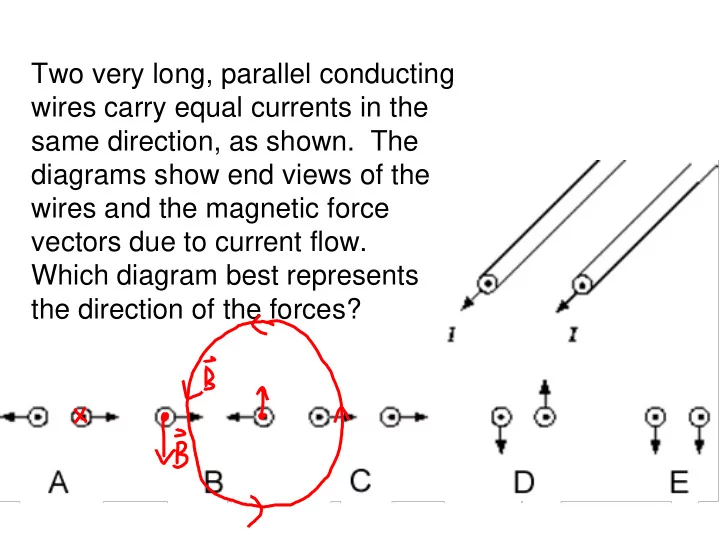

Two very long, parallel conducting wires carry equal currents in the same direction, as shown. The diagrams show end views of the wires and the magnetic force vectors due to current flow. Which diagram best represents the direction of the forces?
Electric Field Lines • Field lines start or end at charges or at infinity. – Lines are directed outwards from positive charges and inward towards negative charges. – # of lines starting or ending at a charge is proportional to the magnitude of that charge (constant of proportionality is arbitrary, i.e. up to you).
Gauss’ Law • The total electric flux (i.e. # of field lines) through a Gaussian (closed) surface is proportional to the charge enclosed by that surface. Q E n ˆ net encl dA E 0
Magnetic field produced by a current loop • Along x axis: 2 ˆ 0 B i 3/ 2 4 2 2 x R 2 ˆ for 0 i x R (or x R ) 3 4 x
Electric field produced by an electric dipole • Along x axis: x ˆ E k p 2 i 2 2 2 x a 2 p ˆ for k i x a (or x a ) 3 x • Electric “dipole moment”: p q 2 a
Gauss’ Law for Magnetism • The total magnetic flux ( B ) through a Gaussian surface is . B n ˆ net dA B
Ampere’s Law • Amperian Curve – A closed curve – It starts and ends at the same point. – E.g. circle, rectangle, but NOT the path from Merrill to Valentine. – It forms the boundary of a surface (there can be many surfaces bounded by the same curve).
Ampere’s Law • If you calculate for all segments of an B dl dl Amperian curve and add them all up, the result is proportional to the amount of current piercing a surface bounded by the curve: B dl I 0 encl
Ampere’s Law and Symmetry • You can use Ampere’s Law to calculate magnetic fields when the situation has some symmetry: – When symmetry determines how B depends on some coordinate. • Choose your Amperian curve to exploit the symmetry so that is easy to calculate on B dl parts of the curve.
Figure 28.9
Recommend
More recommend