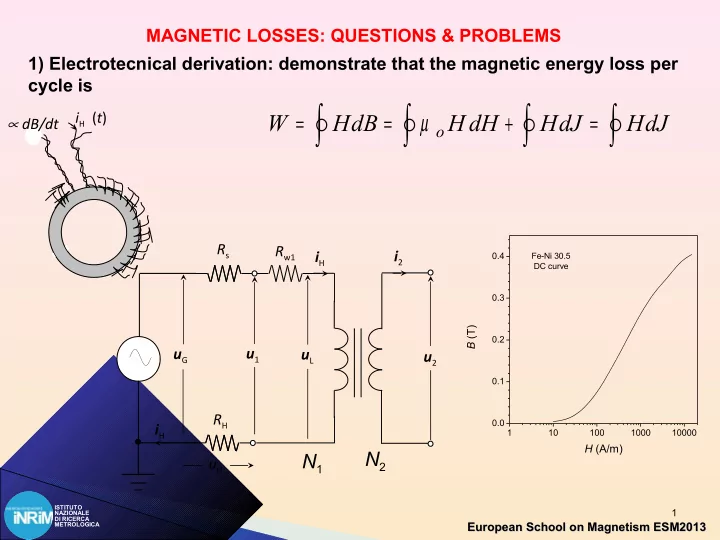
w h db h dh h dj h dj i h t db dt o r s r w1 i 2
play

= = + = W H dB H dH H dJ H dJ i H ( t ) dB/dt - PowerPoint PPT Presentation

Jan 17, 2023 •311 likes •538 views

MAGNETIC LOSSES: QUESTIONS & PROBLEMS 1) Electrotecnical derivation: demonstrate that the magnetic energy loss per cycle is = = + = W H dB H dH H dJ H dJ i H ( t ) dB/dt o R s R w1 i 2 i H 0.4 Fe-Ni

  1. MAGNETIC LOSSES: QUESTIONS & PROBLEMS 1) Electrotecnical derivation: demonstrate that the magnetic energy loss per cycle is ∫ ∫ ∫ ∫ = = µ + = W H dB H dH H dJ H dJ i H ( t ) ∝ dB/dt o R s R w1 i 2 i H 0.4 Fe-Ni 30.5 DC curve 0.3 B (T) 0.2 u 1 u G u L u 2 0.1 R H 0.0 i H 1 10 100 1000 10000 H (A/m) N 2 N 1 u H ISTITUTO ISTITUTO 1 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  2. = + Φ u ( t ) Ri ( t ) d / dt = µ + B H J G H 0 t = 0 B = 0; t = t 0 B = B p t ∫ = 0 E ( t ) u ( t ) i ( t ) dt 0 G H 0 dB = ∫ t t ∫ + = + 0 2 0 E ( t ) Ri ( t ) dt N A i ( t ) dt E U 0 H 1 H R dt 0 0 = i H ( t ) ( l / N ) H ( t ) m 1 Energy delivered to the magnetic system = Al V B HdB dB m t ∫ ∫ = 0 = p U ( t ) V H ( t ) dt V 0 dt 0 0 ∫ ∫ ∫ = µ + H dB H dH H dJ o Energy loss per cycle per unit volume dH T ∫ ∫ µ = µ = H dH H 0 ∫ = W H dJ o o dt 0 ISTITUTO ISTITUTO 2 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  3. 2) Find the energy stored in the gap of a permanent magnet (the exploitable energy during magnet operation) B H m l g H g J m l m 1 ( ) V = − E g BH 2 ISTITUTO ISTITUTO 3 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  4. The whole magnetostatic energy associated with the magnet (energy of formation) N = H = − d H J d µ 0 The sum of the energy stored inside 1 1 ∫ the magnet and the energy stored 2 = − ⋅ = E H J dV N J V ms d µ outside it, possibly confined to a good 2 2 V o extent inside the gap. 1 1 ∫ 2 2 2 = µ = E H dV N J V Energy stored in the material m o d µ 2 2 V o ( ) V 1 = + µ B J H 2 2 = − = − E E E J N N Energy stored in the gap o g ms m d d µ 2 o ( ) 1 1 = − = − + µ E N J J N J V H ( J H ) V 1 g d d 0 µ ( ) V 2 2 = − o E g BH 2 ISTITUTO ISTITUTO 4 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  5. ∫ = − H l H l ⋅ = H dl 0 g g m m B Φ = µ = Φ = H S B S g 0 g m m H m l g H g 1 = µ 2 J m E H V Energy inside the gap g o g g 2 l m 1 1 1 B = µ = µ ⋅ = − µ ⋅ 2 E H V H l H S H l S g 0 g g 0 g g g 0 m m µ 2 2 2 0 1 ( ) V = − E g BH 2 ISTITUTO ISTITUTO 5 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  6. 2) Find the hysteresis loss component versus H p and J p in the Rayleigh region. Find the rotational contribution to the initial permeability a for isotropic distribution of easy axis (small angle rotations). ( H p , J p ) Ni 0.05 = + 2 J aH bH p p p 0.00 J (T) b = + − 2 2 J ( H ) ( a bH ) H ( H H )  p p 2 -0.05 -400 -200 0 200 400 H (A/m) ∫ = W ( H ) J ( H ) dH ISTITUTO ISTITUTO 6 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  7. 2a) Find the hysteresis loss component in the Rayleigh region. b ( H p , J p ) = + − 2 2 Ni J ( H ) ( a bH ) H ( H H )  0.05 p p 2 = + 2 J aH bH p p p 0.00 J (T) ∫ = W ( H ) J ( H ) dH -0.05 The linear terms can be omitted. -400 -200 0 200 400 H (A/m) b b b b H H H H ∫ ∫ ∫ ∫ = − + − 2 p p 2 2 p p 2 W ( H ) H dH H dH H dH H dH ) p p 2 2 2 2 − − − − H H H H p p p p [ ] 1 3 4 = − + + 2 W ( J ) a a 4 bJ = 3 W ( H ) bH p p p 2 6 b 3 1 b 3 2 W = J > > aH bH p p p 3 3 a 4 3 / 2 < < 2 W = aH bH J p p p 3 b ISTITUTO ISTITUTO 7 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  8. 2b) Find the initial permeability associated with rotations. = − µ θ − ϕ + ϕ 2 E M H (cos( ) K sin 0 s 1 H Minimize the energy and find the equilibrium angle ϕ M s ϕ µ θ M H sin θ ϕ ≅ sin 0 s Small oscillations µ θ + M H cos 2 K cos ϕ ≅ 1 0 s 1 K 1 µ θ M H sin ϕ ≅ sin 0 s 2 K 1 µ θ < < M H cos 2 K Small oscillations 0 s 1 ∆ M ≅ θ sin ϕ M sin s ∆ θ µ θ M M sin M H sin χ = ≅ s 0 s H H 2 K 1 µ 2 M χ θ ≅ θ 2 ( ) 0 s sin 2 K 1 ISTITUTO ISTITUTO 8 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  9. Uniform space distribution of easy directions. π θ θ dN 2 sin d θ θ = θ θ p ( ) d sin d = π N 2 π / 2 ∫ θ d θ = p ( ) 1 0 µ 2 M 2 K χ θ ≅ θ 2 ( ) 0 s sin < > = 1 H 2 K K µ M 1 0 s M M π π / 2 / 2 ∫ ∫ 2 M < χ > ≅ θ θ θ = θ θ 2 3 s sin p ( ) d s sin d < χ rot > ≅ s H H 0 0 3 H K K K Fe-(3 wt%)Si, M s = .6 ⋅ 10 6 A/m, K 1 = 38 ⋅ 10 3 J/m 3 , H K = 38.4 ⋅ 10 3 A/m < χ rot > ≅ 28. Examples Mn-Zn ferrite, M s = 3.9 ⋅ 10 5 A/m , K 1 = 50 J/m 3 , H K = 205 A/m, < χ rot > ≅ 1270. 3 ∫ θ θ = θ − θ 3 sin d ( 1 / 3 ) cos cos ISTITUTO ISTITUTO 9 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  10. 3) Find: 1) The complex permeability in a linear material. 2) The relationship with the energy loss. 3) The related Q factor. 4) The equivalent R-L circuit of a ring inductor.  B ′ p µ = δ = ω cos H ( t ) H cos t  p H  p ( ) = ω − δ =  B ( t ) B cos t p B  ′ ′ p µ = δ = δ ω + δ ω sin B cos cos t B sin sin t  p p H  p The 90°-delayed component of the induction is connected with the dissipation of energy. in-phase out-of-phase From the definition of the energy loss per cycle W, we obtain that the power loss per unit volume is dB ( t ) T ∫ [W / m 3 ] = = ⋅ = π δ P Wf f H ( t ) dt f H B sin p p dt 0 ISTITUTO ISTITUTO 10 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  11. J W = π δ H p J sin ′ ′ µ = p δ 0.010 Co 67 Fe 4 B 14.5 Si 14.5 sin J p = 10 mT p H p 0.005 Energy loss under given peak field value ′ ′ 0.000 = π µ 2 J (T) W H [J / m 3 ] p -0.005 Energy loss under given peak polarization value f = 1 MHz ′ ′ µ -0.010 = π 2 W J -1 0 1 [J / m 3 ] p ′ ′ ′ µ + µ 2 2 H (A/m) The quality factor of the inductor is defined as the ratio between the maximum stored energy and the energy dissipated per unit volume during one cycle . 1 E = π δ E B H sin = δ = π E B H cos Q 2 L L p p R p p E 2 R ′ µ = Q ′ ′ µ ISTITUTO ISTITUTO 11 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  12. The equivalent L - R circuit  l  = ω j t I H ( t ) H e = ω  j t I ( t ) H m e  p p  N  = ω − δ j ( t )  B ( t ) B e R s   ω − δ p = ω ⋅ j ( t ) V ( t ) j B e NS δ  p j ω L s I = + ω  V ( t ) R I ( t ) j L I ( t ) L s s s  ω NS B  = p δ + δ V ( t ) (sin j cos ) I ( t ) R s I  I  p i H ( t ) ω  NS B = p δ R sin  s I  p  ω NS B  ω = p δ L cos  s I  p ISTITUTO ISTITUTO 12 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

  13. A ring core inductor of cross-sectional area S , mean diameter i H ( t ) D , and number of turns N.  B ′ µ = p δ NI cos  π D p p = H = H I H  π p D p p N  B  ′ ′ µ = p δ sin  H  p ω  NS B  ω 2 N S B = p δ R sin  p = δ R sin  s I s π  DH  p  p  2  N S ω NS B ′ ′ = ω µ  R ω 2 N S B   ω = p δ L cos  s π ω = p δ D L cos  s  I  s  π DH p  2 p N S  ′ ω = ω µ L  s  π D ISTITUTO ISTITUTO 13 NAZIONALE NAZIONALE DI RICERCA DI RICERCA European School on Magnetism ESM2013 European School on Magnetism ESM2013 METROLOGICA METROLOGICA

Recommend

More recommend