Visibility Graphs of Staircase Polygons Yulia Alexandr Mentor: - PowerPoint PPT Presentation
Visibility Graphs of Staircase Polygons Yulia Alexandr Mentor: Prof. James Abello NSF grant CCF-1559855 Let me remind you We consider a simple non-degenerate collection of points in the plane that produces a polygon v 1 u 1 In
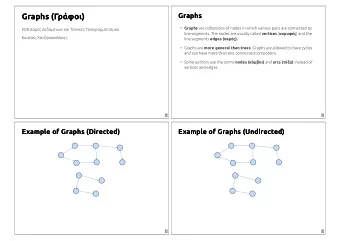
Visibility Graphs of Staircase Polygons Yulia Alexandr Mentor: Prof. James Abello NSF grant CCF-1559855
Let me remind you… • We consider a simple non-degenerate collection of points in the plane that produces a polygon v 1 u 1 • In particular, we look at staircase polygon paths u 2 v 2 • Two vertices of a polygon are called internally visible u 3 if the closed line segment between them is either an v 3 edge of the polygon or lies entirely in the interior of u 4 the polygon (Abello et al) v 4 • The visibility graph of a polygon is a graph whose v 5 vertex set is the same as the vertex set of the polygon v 0 and whose edges are the straight-line segments between internally visible vertices
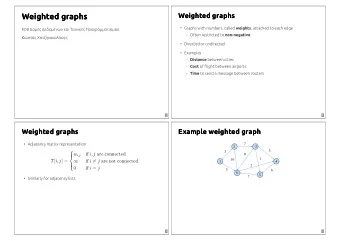
Balanced Tableau • Hook of a cell is the collection of cells that includes the chosen cell with all the cells above it and all the cells to the right 1 • Mate cells with respect to the chosen cell 2 1 2 • A tableau is balanced if the value of every cell lies in 3 3 8 2 between every pair of mate cells in its hook 4 10 9 4 3 • (!) Tableau represents slope ranks in a staircase path on n vertices 5 6 5 7 5 4
Local Max (Min) Rule • Apply the rule to obtain the 1 1 adjacency matrix 2 8 1 1 3 9 10 1 1 1 0 1 1 6 5 0 7 1 4
Problem Statement Problem Statement: Input: A balanced tableau T n Output: Build a staircase polygon s.t. its visibility graph is isomorphic to localmax (T n ) ? • The problem is known to be PSPACE ? • We also want to know whether it is NP or P
What I tried: • Random Stuff L • Convex Hull Approach L • Inductive Approach L / J 😎 • Visibility Regions Approach
Visibility Regions Approach • Starts building from the middle • Takes advantage of unboundedness 1 • Forms a visibility region to place each new vertex 2 2 1 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 1 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 1 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 0 1 1 5 5 0 1
Example 1 2 3 1 2 2 1 4 3 3 1 1 4 4 1 1 1 5 0 1 1 5 5 0 1
Too good to be true… • Can visibility regions be empty?
Too good to be true… • Can visibility regions be empty? Yep.
Too good to be true… • Can visibility regions be empty? Yep. • Why?
Too good to be true… • Can visibility regions be empty? Yep. • Why? Research is hard.
Too good to be true… • Can visibility regions be empty? Yep. • Why? Research is hard. • What makes them empty?
Too good to be true… • Can visibility regions be empty? Yep. • Why? Research is hard. • What makes them empty? Not preserving slope ranks of farthest seen vertices!! 1 1 1 2 2 1 1 2 2 8 3 3 3 2 8 1 1 9 3 10 4 4 3 9 10 1 1 1 4 4 5 5 6 5 7 0 1 1 0 5 4 1 5
What I proved: • Regions are never empty as long as we preserve slope ranks of farthest seen vertices at each stage of construction • Concave-concave (convex-convex) • Concave-convex (convex-concave) • General case
What I proved: • Regions are never empty as long as we preserve slope ranks of farthest seen vertices at each stage of construction • Concave-concave (convex-convex) • Concave-convex (convex-concave) • General case • It is always possible to preserve slope ranks of farthest seen vertices
What’s left: • Determine complexity • Double check and polish proofs • Finalize results for publication
Acknowledgements: • Prof. James Abello • DIMACS and Prof. Gallos • NSF grant CCF-1559855
Thanks! J • References: • [1] Abello et al, Visibility Graphs of Staircase Polygons and the Weak Bruhat Order, I: from Visibility Graphs to Maximal Chains* . Discrete & Computational Geometry. 1995. 331-358.
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.




![The Touring Polygons Problem (TPP) [Dror-Efrat-Lubiw-M]: Given a sequence of k polygons in the](https://c.sambuz.com/895801/the-touring-polygons-problem-tpp-s.webp)