Virtual Inertia Emulation and Placement in Power Grids S eminaire - PowerPoint PPT Presentation

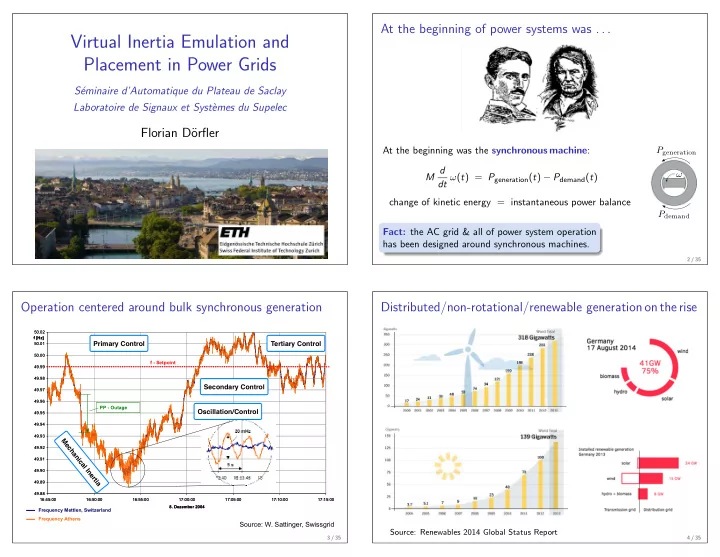
At the beginning of power systems was . . . Virtual Inertia Emulation and Placement in Power Grids S´ eminaire d’Automatique du Plateau de Saclay Laboratoire de Signaux et Syst` emes du Supelec Florian D¨ orfler At the beginning was the synchronous machine : P generation M d ω dt ω ( t ) = P generation ( t ) − P demand ( t ) change of kinetic energy = instantaneous power balance P demand Fact: the AC grid & all of power system operation has been designed around synchronous machines. 2 / 35 Operation centered around bulk synchronous generation Distributed/non-rotational/renewable generation on the rise 50.02 50.02 f [Hz] f [Hz] Primary Control Tertiary Control 50.01 50.01 50.00 50.00 f - Setpoint 49.99 49.99 49.98 49.98 Secondary Control 49.97 49.97 49.96 49.96 PP - Outage Oscillation/Control 49.95 49.95 PS Oscillation 49.94 49.94 49.93 49.93 Mechanical Inertia 49.92 49.92 49.91 49.91 49.90 49.90 49.89 49.89 49.88 49.88 16:45:00 16:45:00 16:50:00 16:50:00 16:55:00 16:55:00 17:00:00 17:00:00 17:05:00 17:05:00 17:10:00 17:10:00 17:15:00 17:15:00 8. Dezember 2004 8. Dezember 2004 Frequency Mettlen, Switzerland Frequency Athens Source: W. Sattinger, Swissgrid Source: Renewables 2014 Global Status Report 3 / 35 4 / 35

A few (of many) game changers . . . Fundamental challenge: operation of low-inertia systems synchronous generator new workhorse scaling We slowly loose our giant electromechanical low-pass filter: P generation M d ω dt ω ( t ) = P generation ( t ) − P demand ( t ) change of kinetic energy = instantaneous power balance P demand location & distributed implementation Almost all operational problems can principally be resolved . . . but one (?) 5 / 35 6 / 35 Low-inertia stability: # 1 problem of distributed generation Virtual inertia emulation devices commercially available, required by grid-codes or incentivized through markets 2001 2002 2003 2004 2005 2006 2007 2008 !""" #$%&'%(#!)&' )& *)+"$ ','#"-'. /)01 23. &)1 2. -%, 2456 5676 2009 30000 2010 !"#$%&'"'() %* +$,(-.'() /'-#%(-' !89:;8;<=><? />@=AB: !<;@=>B >< CD!EFGBH;I 25000 .( 0.1$%2$.3- 4-.(2 5.$)6,7 !('$)., +><I *JK;@ E;<;@B=>J< 20000 8.".-9 :%(. ! "#$%&'# (&)*&+! ,--- ; :6$<,(,$,<,(, =%%77, ! (&)*&+! ,--- ; ,(3 Duration [s] 06>67 ?@ ?9,(3%$>,$ ! (&)*&+! ,--- -JLB88BI@;MB DBNLB@> -J?LBIIB8 %@B<> ! "#$%&'# (&)*&+! ,--- . B<I "LBO D1 ":F'BBIB<P ! "&'./+ (&)*&+! ,--- 15000 Events [-] !"#$%&'()*+,-+#'"(./#0*/1(2-33/*04($(5&*0-$1(( Virtual synchronous generators: A survey and new perspectives 10000 6#+*0&$(7*/8&9+9(:"(!&;0*&:-0+9(<#+*="(20/*$=+( Hassan Bevrani a,b, ⇑ , Toshifumi Ise b , Yushi Miura b 5000 a Dept. of Electrical and Computer Eng., University of Kurdistan, PO Box 416, Sanandaj, Iran 0/(6;/1$0+9(7/>+*(2";0+%;(( b Dept. of Electrical, Electronic and Information Eng., Osaka University, Osaka, Japan 0 !""" #$%&'%(#!)&' )& *)+"$ ','#"-'. /)01 23. &)1 2. -%, 2456 ?$-0@&+*(!+1&11+A( !"#$"%&'())) A(B*-#/()*$#C/&;A( *"+,-%'!"#$"%&'())) A($#9(?&11+;(D$1$*$#=+( Number * 10 !789:;< "=>?<:;@7 (@7:9@? ':9<:8AB C@9 Months of the year !"#$%&#'$%()*+'",'"%-#,.%/#",012%3#*',#4% /'(DE/F( #9<7G=;GG;@7 'BG:8=G # frequency violations in Nordic grid 5,)"16'% Number * 10 Duration H;8I8; JK>. (<=LI8?? F1 M@@:K. N9<;7 *1 %O<=. %7O98P H1 $@GQ@8. <7O (K9;G N1 M9;AK: 7898:%+1*%;'<'*=''4> ? %@%58;8A8%$'%A11* ? @% !"#$%&'("()"&*'+,,, @%98%/1"'21 B %1*$%38%/#<<4.'" C @% (source: ENTSO-E) same in Switzerland (source: Swissgrid) !"#$%&'("()"&'+,,, % M d dt ω ( t ) = P generation ( t ) − P demand ( t ) . . . essentially D-control inertia is shrinking, time-varying, & localized, . . . & increasing disturbances ⇒ plug-&-play (decentralized & passive), grid-friendly, user-friendly, . . . Solutions in sight: none really . . . other than emulating virtual inertia through fly-wheels, batteries, super caps, HVDC, demand-response, . . . it eal ⇒ today: where to do it? how to do it properly? 7 / 35 8 / 35 15

Outline Introduction Novel Virtual Inertia Emulation Strategy inertia emulation Optimal Placement of Virtual Inertia Conclusions Classification & choice of actuators Inertia emulation & virtual synchronous machines 1 naive D-control on ω ( t ): M d dt ω ( t ) = P generation ( t ) − P demand ( t ) 2 more sophisticated emulation of virtual synchronous machine Contents lists available at ScienceDirect Electrical Power and Energy Systems journal homepage: www.elsevier.com/locate/ijepes Virtual synchronous generators: A survey and new perspectives Hassan Bevrani a,b, ⇑ , Toshifumi Ise b , Yushi Miura b a Dept. of Electrical and Computer Eng., University of Kurdistan, PO Box 416, Sanandaj, Iran b Dept. of Electrical, Electronic and Information Eng., Osaka University, Osaka, Japan 3 everything in between . . . and much more . . . (source: Stephan Masselis) ⇒ by measuring AC current/voltage/power/frequency ⇒ software model of virtual machine provides converter setpoints each of these (& far more) have been proposed for virtual inertia emulation ⇒ actuation via modulation (switching) or DC injection (batteries etc.) 9 / 35 10 / 35

Challenges in real-world converter implementations Averaged inverter model Real Time Simulation of a Power System with i αβ R L i load Contents lists available at ScienceDirect DC cap & AC filter equations: VSG Hardware in the Loop Electrical Power and Energy Systems i x i c v dc = − G dc v dc + i dc − 1 + + journal homepage: www.elsevier.com/locate/ijepes Vasileios Karapanos, Sjoerd de Haan, Member , IEEE , Kasper Zwetsloot 2 m ⊤ i αβ Faculty of Electrical Engineering, Mathematics and Computer Science C dc ˙ Delft University of Technology Delft, the Netherlands Virtual synchronous generators: A survey and new perspectives v αβ i dc v x E-mails: vkarapanos@gmail.com, v.karapanos@tudelft.nl, s.w.h.dehaan@tudelft.nl G dc C dc C Hassan Bevrani a,b, ⇑ , Toshifumi Ise b , Yushi Miura b C ˙ v αβ = − i load + i αβ To better study and witness the effects of virtual inertia, the a Dept. of Electrical and Computer Eng., University of Kurdistan, PO Box 416, Sanandaj, Iran Abstract- The method to investigate the interaction between a hardware of a real VSG should be tested within a power b Dept. of Electrical, Electronic and Information Eng., Osaka University, Osaka, Japan Virtual Synchronous Generator (VSG) and a power system is system. Investigating the interaction between a real VSG and − − i αβ = − Ri αβ + 1 presented here. A VSG is a power-electronics based device that a power system is not easy as a power system cannot be L ˙ 2 mv dc − v αβ 1 delays in measurement acquisition, signal processing, & actuation modulation: i x = 1 2 m ⊤ i αβ , v x = 1 passive: ( i dc , i load ) → ( v dc , v αβ ) 2 mv dc 2 accuracy in AC measurements (averaged over ≈ 5 cycles) θ 3 constraints on currents, voltages, power, etc. model of a ˙ θ = ω � − sin( θ ) � synchronous ω = − D ω + τ m + i ⊤ M ˙ αβ L m i f 4 guarantees on stability and robustness cos( θ ) generator i f C ˙ v αβ = − G load v αβ + i αβ � − sin( θ ) � L s ˙ i αβ = − Ri αβ − v αβ − ω L m i f cos( θ ) today: use DC measurement, exploit analog storage, & passive control �������������������������������������� ���� 11 / 35 12 / 35 See the similarities & the differences ? i αβ R L i load DC cap & AC filter equations: i x i c v dc = − G dc v dc + i dc − 1 + + 2 m ⊤ i αβ C dc ˙ v αβ v x standard power electronics control would continue by i dc G dc C dc C C ˙ v αβ = − i load + i αβ − − i αβ = − Ri αβ + 1 L ˙ 2 mv dc − v αβ 1 constructing voltage/current/power references (e..g, droop, synchronous machine emulation, etc.) modulation: i x = 1 2 m ⊤ i αβ , v x = 1 passive: ( i dc , i load ) → ( v dc , v αβ ) 2 mv dc 2 tracking these references at the converter terminals θ typically by means of cascaded PI controllers model of a ˙ θ = ω � − sin( θ ) � synchronous ω = − D ω + τ m + i ⊤ M ˙ αβ L m i f cos( θ ) generator let’s do something different (smarter?) today . . . i f C ˙ v αβ = − G load v αβ + i αβ � − sin( θ ) � L s ˙ i αβ = − Ri αβ − v αβ − ω L m i f cos( θ ) 13 / 35 14 / 35