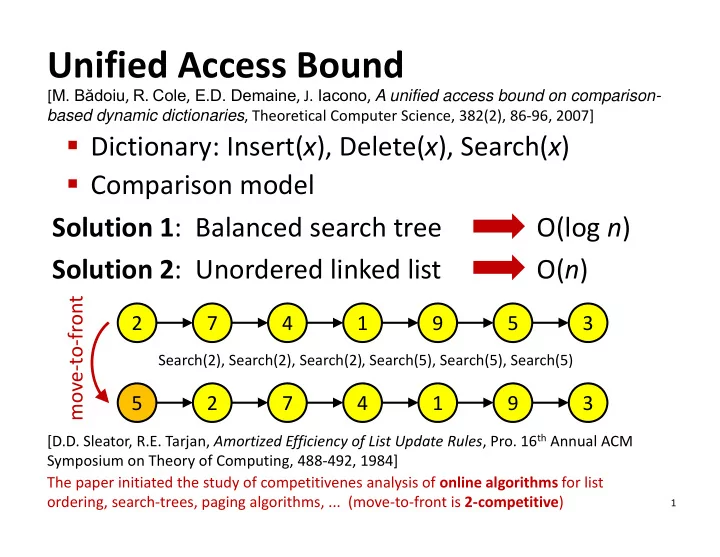

Unified Access Bound [ M . B ă doiu , R . Cole , E . D. Demaine , J. Iacono , A unified access bound on comparison- [ , , , , p based dynamic dictionaries , Theoretical Computer Science, 382(2), 86 ‐ 96, 2007] � Dictionary: Insert( x ), Delete( x ), Search( x ) � Comparison model Solution 1 : Balanced search tree O(log n ) Solution 2 : Unordered linked list O( n ) nt ve ‐ to ‐ fro 2 7 4 1 9 5 3 Search(2), Search(2), Search(2), Search(5), Search(5), Search(5) mov 5 2 7 4 1 9 3 [D.D. Sleator, R.E. Tarjan, Amortized Efficiency of List Update Rules , Pro. 16 th Annual ACM Symposium on Theory of Computing, 488 ‐ 492, 1984] The paper initiated the study of competitivenes analysis of online algorithms for list ordering, search ‐ trees, paging algorithms, ... (move ‐ to ‐ front is 2 ‐ competitive ) 1
Access sequences ‐ examples � X 1 = 1 2 3 X 1 = 1, 2, 3, ..., n , 1, 2, 3, ..., n , 1, 2, 3, ... n 1 2 3 n 1 2 3 � X 2 = 1, n , 1, n , 1, n , ... � X 3 = 1, n /2, 2, n /2+1, 3, n /2+2, ..., n /2, n , 1, ... /2 2 /2 3 /2 2 /2 2
Access sequence X = ( x 1 , x 2 , ..., x m ) � Static optimal O(log (1/ p ( x i ))) / Finger � Sequential ‐ access bound O(1) search t � Static finger bound O(log d i ( f , x i )) � Dynamic finger bound Dynamic finger bound O(log d ( x x )) O(log d i ( x i , x i ‐ 1 )) tree � Working set bound O(log w i ( x i )) � Unified bound f d b d O(min y ∈ Si log( w i ( y )+ d i ( x i , y ))) ( l ( ( ) d ( ))) d i ( f , x i ) d i ( f , x i ) d i ( x i , x i 1 ) d i ( x i , x i ‐ 1 ) Sorted list f x i x i ‐ 1 Move ‐ to ‐ front list Move to front list x i w i ( x i ) 3
Splay trees (amortized) 1 1 � Static optimal O(log (1/ p ( x i ))) / 2 � Sequential ‐ access bound O(1) 1 � Static finger bound O(log d i ( f , x i )) 3 Dynamic finger bound � Dynamic finger bound O(log d ( x x )) O(log d i ( x i , x i ‐ 1 )) 1 � Working set bound O(log w i ( x i )) Open Open � Unified bound f d b d O(min y ∈ Si w i ( y )+ d i ( x i , y )) ( ( ) d ( )) 1 [D D Sleator R E Tarjan Self ‐ Adjusting Binary Search Trees J ACM 32(3) 652 ‐ 686 1985] 1 [D.D. Sleator, R.E. Tarjan, Self ‐ Adjusting Binary Search Trees , J. ACM 32(3), 652 ‐ 686, 1985] 2 [R.E. Tarjan, Sequential access in play trees takes linear time . Combinatorica 5(4), 367 ‐ 378, 1985] 3 [R. Cole, B. Mishra, J.P. Schmidt, A. Siegel, On the Dynamic Finger Conjecture for Splay Trees . Part I: Splay Sorting log n ‐ Block Sequences . SIAM J. Computing, 30(1), 1 ‐ 43, 2000] [R. Cole, On the Dynamic Finger Conjecture for Splay Trees. Part II: The Proof . SIAM J. Computing, 30(1), 44 ‐ 85, 2000] 4
Static optimality [T.C. Hu, A.C. Tucker, Optimal computer search trees and variable ‐ length alphabetic codes , SIAM Journal on Applied Mathematics 21 (4), 514–532, 1971] [D.E. Knuth, Optimum binary search trees , Acta Informatica 1, 14–25, 1971] Split ≤ ½ weight both children D ⇒ Depth i subtree weight ≤ (½) i 1.0 ⇒ Depth x i ≤ log(1/ p ( x i )) ⇒ Static optimal ⇒ Static optimal G G A A 0.23 0.17 B F H 0.07 0.11 0.10 C J E 0.02 0.03 0.04 I I 0.01 x i A B C D E F G H I J p( x i ) 0.10 0.05 0.02 0.60 0.03 0.08 0.02 0.06 0.01 0.03 Construction: Compute prefix sums + Exponential search ⇒ O( n ) 5
Working ‐ set structure [ M . B ă doiu , R . Cole , E . D. Demaine , J. Iacono , A unified access bound on comparison- [ , , , , p based dynamic dictionaries , Theoretical Computer Science, 382(2), 86 ‐ 96, 2007] T 3 T 2 T T 1 T 0 L 0 L 1 L 2 L 3 w j � L = L 0 + L 1 + ∙∙∙ = move ‐ to ‐ front list L L 0 + L 1 + move to front list � | L i |=2 2 i Search( T 0 ) + ∙∙∙ + Search( T j ) = log(2 20 ) + ∙∙∙ + log(2 2 i ) � T i = search tree over L i T h t L ≤ 4 ∙ log(2 2 i ‐ 1 ) ≤ 4 ∙ log w j 2 i 1 � Insert, Delete = O(log n ), Search = O(log w j ) 6
Unified structure [ M . B ă doiu , R . Cole , E . D. Demaine , J. Iacono , A unified access bound on comparison- [ , , , , p based dynamic dictionaries , Theoretical Computer Science, 382(2), 86 ‐ 96, 2007] Search trees of a subset Search trees of a subset of the elements T 3 T 2 T 1 T ( ) T 0 Finger search tree over all elements Lemma 7 w i ( y ) ≤ 2 2 k and x and y rank distance ≤ 2 2 k , then 2 k d k d h F x within rank distance ( k +4)2 2 k of some y ’ ∈ T 0 ∪ ∙∙∙ ∪ T k predecessor successor 7
Recommend
More recommend