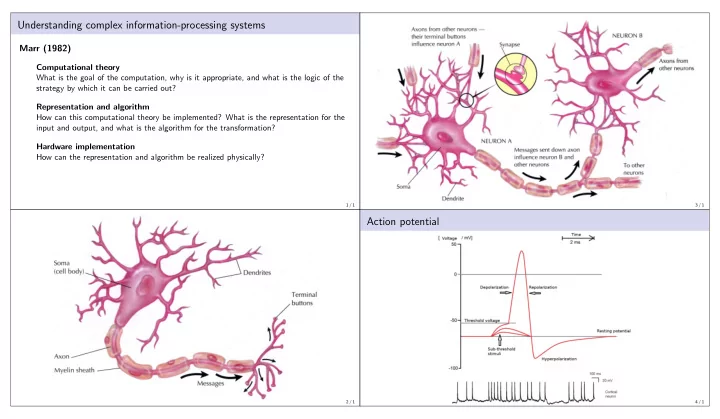

Understanding complex information-processing systems Marr (1982) Computational theory What is the goal of the computation, why is it appropriate, and what is the logic of the strategy by which it can be carried out? Representation and algorithm How can this computational theory be implemented? What is the representation for the input and output, and what is the algorithm for the transformation? Hardware implementation How can the representation and algorithm be realized physically? 1 / 1 3 / 1 Action potential 2 / 1 4 / 1
Types of units Binary threshold unit � = a i w ij + e j n j i � 1 if n j > θ j a j = 0 otherwise If “bias” b j = − θ j , this is the same as � 1 if n j > 0 � = a i w ij + e j + b j a j = n j 0 otherwise i Will generally omit b j and e j in equations Bias b j can be treated as weight w ij from special unit with fixed activation a i = 1. External input e j can be treated as incoming activation a i across connection with fixed weight w ij = 1. 5 / 1 7 / 1 Notation � Linear units a j = n j = a i w ij i Rectified linear units (ReLUs) i , j indices of units ( i sending, j receiving) a j activation of unit j a j = max (0 . 0 , n j ) n j summed net input to unit j w ij weight on connection from unit i to unit j external input to unit j e j Sigmoidal (“logistic”, “semi-linear”) units threshold for unit j θ j b j bias (tonic input) to unit j (= − θ j ) 1 a j = σ ( n j ) = 1 + exp ( − n j ) Binary stochastic units 1 p ( a j = 1) = 1 + exp ( − n j ) 6 / 1 8 / 1
Continuous time-averaged (cascaded) units [two alternatives] n [ t ] a [ t − 1] (1 − τ ) n [ t − 1] � = τ w ij + j i j i � � a [ t ] n [ t ] (1 − τ ) a [ t − 1] = τ σ + j j j Interactive activation (Jets & Sharks model; Schema model; McClelland & Rumelhart letter/word model) n [ t ] a [ t − 1] w ij + e [ t ] � = j i j i � � n [ t ] max − a [ t − 1] if n [ t ] > 0 a [ t ] (1 − decay ) a [ t − 1] j j j = + j j n [ t ] � a [ t − 1] � − min otherwise j j decay = 0 . 1 max = 1 . 0 min = − 0 . 2 9 / 1
Recommend
More recommend