trapped - PDF document

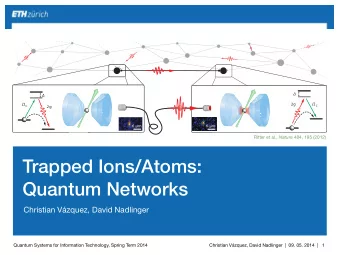
Outline: ����������������������� ����� • trapped ions • ion traps ��������������������� • degrees of freedom • state detection • interactions with lasers • decoherence we'd like to remove • motional • spin • decoherence we can cause • engineered reservoirs Frontiers of Quantum Decoherence - August 14, 2006 Fields Institute, University of Toronto Brian King http://physwww.mcmaster.ca/~kingb/King_B_h.html Linear ion traps: Ion traps in situ : • McMaster ion trap: 25 Mg + U 0 U 0 • axial confinement - static! V 0 , Ω V 0 , Ω ions α ~ 1 (geom.) laser beams radial • radial confinement -dynamic! ions a l x i a Ω Rf ≈ 14 MHz, U 0,DC ≈ 200 V, V 0,RF ≈ 300 V � ω z ≈ 1.4 MHz, ω R ≈ 4.3 MHz β ~ 1 (geom.) • ω ω r < Ω Ω RF ω ω Ω Ω " m ic ro m o tio n" " s e c u la r" m o tio n 0 2 4 tim e 6 8 1 0 • micromotion small, at different freq. after D. Berkeland, Rev. Sci. Inst. 73 , 2856 (02) 1

Internal states - quasi- Internal states - quasi- spin-½ (qubit) : spin-½ (qubit) : 1. long-lived electronic states: 2. ground-state hyperfine levels: Be + (313 nm), γ/2π = 43 MHz P 3/2 Mg + (280 nm), τ = 3.5 ns P 1/2 Ca + , Sr + , Ba + , Hg + P 3/2 Cd + (215 nm) ~ 10 GHz P 1/2 866 nm,1092 nm 280 nm k 1 ≈ k 2 ,  1 � (or ↑ � ) 397 nm ∆ k ≈ 2k (90°) D 5/2 Energy 422 nm τ = 1 s Energy τ = 345 ms 194 nm 729 nm D 3/2 τ = 90 ms  1 � (or ↑ � ) 674 nm ultra-stable 282 nm S 1/2 1.78 GHz laser (τ > 10,000 y. )  0 � (or ↓ � ) S 1/2  0 � (or ↓ � ) Mg + • single-photon transitions: stable laser required • 2-photon, stimulated-Raman transitions: RF stability External states (motion): State preparation: • micromotion ignorable � secular motion • electronic: • optical qubit - kT � free! • secular motion: ~ harmonic osc. • hyperfine qubit: optical pumping • vibrational: Doppler, sideband, etc. laser cooling (not to scale!) • laser cooling → quantum harmonic oscillator State Detection: ~ electromagnetic field mode... • cycling transition - excited state decays back to |0 � � � � • multiple ions (cold): Γ ~ 1 MHz “  0 � ” “  1 � ” • each collective mode ≡ 1 harmonic oscillator  1 �  1 � i det.  0 � GHz - THz “1010” laser beam  0 � i 2

Laser coupling: Laser coupling: • H I ∝ µ · E 0 e i ( kz - ω L t ) 1. Energy? detuning of laser(s) from resonance! • if ion vibrates, interaction strength modulated ω L = ω 0 : "carrier" − n 0,i ↔ n 1,i • H I ∝ µ · E 0 e i [ k z max cos ( ω z t ) - ω L t ] ω L = ω 0 + ω z : "blue sideband" − n 0,i ↔ n+1 1,i Classically: µ · E 0 Σ m i m J m ( k z max ) e im ω z t e − i ω L t ω L = ω 0 + ω z : "red sideband" − n 0,i ↔ n − 1 1,i sidebands! ~ 1 MHz can change ω z ...etc. (higher sidebands...) motion! ω L – ω 0  1 � i 0 • coupling strength: H I ∝ ½ µ E 0 (S + + S − ) e i [ k z 0 (a + a † ) − ω L t ] ω 0 Quantum: = Ω (S + + S − ) e i k z 0 (a + a † ) e − i ω L t  0 � i int. pic. : Ω (S + e i ω 0 t + H.C. ) e i k z 0 (a ) e − i ω L t e − i ω z t e i ω z t + a † Coupling to only the Laser coupling: motion: • ion is charged (!): E ↔ force • coupling strength determined by E gradients (dipole!) • ion is harmonically bound : resonance ( ω z ) 2. momentum... • classical force E 0 sin ( ω t −ϕ ) → displacement • coupling strength ~ Lamb-Dicke parameter wavevector • alternative: co-propagating lasers, detuning δω photon momentum ground state atom SHO momentum wavefcn width • " walking standing wave " 1. induces dipole moment • Lamb-Dicke parameter ~ p match to SHO 2. drives ion motion through dipole force • atom recoil vs. trap recoil! different dipole moment for | 0 � , | 1 � ? − µ + • "cat state" | 0 , α � + | 1 , β � 3

Motional decoherence - Motional decoherence - heating: heating: L Deslauries et al. , quant-ph/0602003 ('06); C Monroe et al. , PRL 75 , 4011 ('95); DJ Wineland et al. , J. Res. NIST 103 , 259 ('98); L Deslauries et al. , quant-ph/0602003 ('06); C Monroe et al. , PRL 75 , 4011 ('95); DJ Wineland et al. , J. Res. NIST 103 , 259 ('98); QA Turchette, et al. PRA 61 , 063418 ('00); etc... QA Turchette, et al. PRA 61 , 063418 ('00); etc... • experimental insight: • "historical" problem: when cooled to | n=0 � , motion heats • 1 trap, 1 load, varying trap size (measure sidebands) • remark: ω z = 2 π × 10 MHz � λ EM = 30 m! • L Deslauries et al. , quant-ph/0602003 ('06) � lumped-circuit analysis of electromagnetic field − 3.47 ± 0.16 z trap 1. ~ z trap � blackbody radiation ≡ Johnson noise − 2 ) 2. not blackbody ( z trap SE ( ω ) ~ ω z − 1.8 ± 0.4 remark: motion only sensitive to noise at (near) ω z • 3. ↓ 10× for T ↓ 2× (blackbody ω z − 1 ) • rate too high for blackbody − fluctuating patch fields? 500 400 heating rate dn/dt (s − 1 ) heating rate dn/dt (s − 1 ) τ sys ~ 1 − 100 µ s 300 helpful(?) technical changes: • 200 1. shield trap electrodes from atom source 100 2. photoionization loading (M Drewsen) 50 NIST < 1 /(4 ms); IBM 1/(10 ms); Innsbruck 1/(190 ms); Michigan 1/(40 ms) z trap ( µ m ) trap freq. ( MHz ) Ramsey expt.: Spin decoherence: • superpositions - how do we characterize phase ? • spontaneous emission • use states with small energy separation or long lifetime laser intens. Γ • environmental fluctuations (B - Zeeman shift )  1 � • use field-insensitive states t R = 4 s! det. t R = 4 ms  0 � t C Langer et al. , PRL 95 , 060502 ('05) T/2, phase φ : t R : T/2: phase evolves 9 Be + , 2 S ½ create try to undo (Schrodinger) superposition superposition! vs. stable laser phase 1.0 1 superposition of carrier: spin loss of visibility 0.5 � decoherence spin/motion -eg. superposition 0.0 ( π /2 pulse) φ τ > 10 s sidebands -30 -20 -10 0 10 20 30 4

Spin decoherence - Engineered reservoirs I: DFS's: H Häffner, et al. , Appl. Phys. B 81 , 151 ('05); C Langer et al. , PRL 95 , 060502 ('06) Myatt et al. , Nature 403 , 269 ('00); Turchette et al. , PRA 62 , 053807 ('00) • encode 1 qubit/pseudospin in 2 ( with symmetry ): 1. amplitude reservoir (high- T ): ξ p • prepare Bell states : • |10 � and |01 � are degenerate: insensitive to global ∆ B x NIST |0, α � + |1, β � • hyperfine levels 2.5 MHz Gaussian noise centred at 10.25 MHz ( ≈ν z ) 300 ms 1 s 2 s • cat state : background noise : sup. of number states : Innsbruck prepare here P 3/2 P 1/2 unstable , so D 5/2 D 3/2 +1/2 move down here! − 1/2 S 1/2 Engineered reservoirs I: Engineered reservoirs II: Myatt et al. , Nature 403 , 269 ('00); Turchette et al. , PRA 62 , 053807 ('00) Poyatos, et al. , PRL 77, 4728 ('96); Myatt et al. , Nature 403 , 269 ('00); Turchette et al. , PRA 62 , 053807 ('00) 2. phase reservoir (high- T ): 1. zero-temperature reservoir: red sideband + spont. em. p 9 Be + qubit: | ↑ � ≡ |1 � has • lifetime ~ 10,000 y x � add laser resonant with 2 P 1/2 | α , ↑ � + | −α , ↓ � • modulate trap strength with ( Γ / 2 π = 19 MHz ), strength Ω D 2.5 MHz Gaussian 1-100 kHz expt. ~ 1 ms � one phase/shot γ eff ~ Ω D ²/ Γ • random shot to shot sup. of number states : cat state : adjustable ratio Ω rsb : γ eff of • coherent to incoherent coupling 5

Engineered reservoirs III Engineered reservoirs II: (?): Poyatos, et al. , PRL 77, 4728 ('96); Myatt et al. , Nature 403 , 269 ('00); Turchette et al. , PRA 62 , 053807 ('00) Poyatos, et al. , PRL 77, 4728 ('96) |0 � � � + |2 � � � , T = 0 reservoir : � � • different couplings → different reservoirs γ eff << Ω rsb → more exotic "ground states" 1. 2 lasers ω 0 ± ω z : squeezed vacuum coupling γ eff >> Ω rsb µ = ν � x- coupling, position pointer states • 2. 2 lasers ω 0 − ω z , ω 0 − 2 ω z : • Schrödinger-cat pointer states! Experimental Conclusions: demonstration: • example: Rabi flopping on carrier: • trapped ions: qubit and harmonic oscillator systems • experiment: • low decoherence repeat, change t • controllable coupling via lasers 1. trap atom 2. atom → ground state |0 � • motion: natural ("anomalous") decoherence • fluctuating ( patch? ) fields 3. turn on coupling laser for time t • reduced to acceptable levels ( for now... ) 4. turn on detection laser: look for light det. • spin: ("anomalous") decoherence |0 � • B -independent transitions → ~ 10 s (~ 10 5 τ op ) |0 � + |1 � Avg # counts 0 10 20 30 • decoherence-free subspaces: superpositions for > 10 s 10 8 0 10 20 30 6 • control of "engineered" reservoirs 4 |1 � arb. combination 2 • study models/dynamics of decoherence in controlled way 0 of |0 � � � � , |1 � � � � ! 0 1 2 3 4 5 0 10 20 30 t ( µ sec) 6