Transformations Rotations Reflections Dilations Symmetry - PDF document

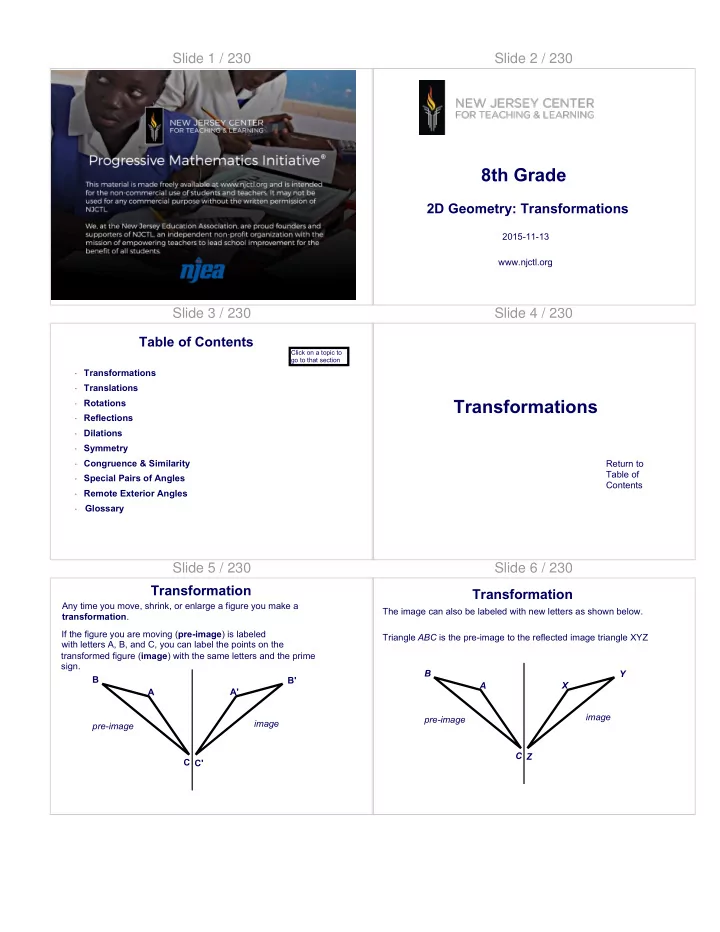
Slide 1 / 230 Slide 2 / 230 8th Grade 2D Geometry: Transformations 2015-11-13 www.njctl.org Slide 3 / 230 Slide 4 / 230 Table of Contents Click on a topic to go to that section · Transformations · Translations Transformations · Rotations · Reflections · Dilations · Symmetry · Congruence & Similarity Return to Table of · Special Pairs of Angles Contents · Remote Exterior Angles Glossary · Slide 5 / 230 Slide 6 / 230 Transformation Transformation Any time you move, shrink, or enlarge a figure you make a The image can also be labeled with new letters as shown below. transformation . If the figure you are moving ( pre-image ) is labeled Triangle ABC is the pre-image to the reflected image triangle XYZ with letters A, B, and C, you can label the points on the transformed figure ( image ) with the same letters and the prime sign. B Y B B' A X A A' image pre-image image pre-image C Z C C'

Slide 7 / 230 Slide 8 / 230 Transformations There are four types of transformations in this unit: · Translations · Rotations · Reflections Translations · Dilations The first three transformations preserve the size and shape of the figure. Therefore, both the pre-image and image will be congruent . Congruent figures are same size and same shape. In other words: Return to If your pre-image is a trapezoid, your image is a congruent Table of trapezoid. Contents If your pre-image is an angle, your image is an angle with the same measure. If your pre-image contains parallel lines, your image contains parallel lines. Slide 9 / 230 Slide 10 / 230 Translation Translations A translation is a slide that moves a figure to a different position (left, right, up or down) without changing its size or shape and without flipping or turning it. You can use a slide arrow to show the direction and distance of the movement. Slide 11 / 230 Slide 12 / 230 Translation Translation This shows a translation of pre-image ABC to image Click for web page A'B'C'. Each point in the pre-image was moved right 7 and up 4.

Slide 13 / 230 Slide 14 / 230 To complete a translation, move each point of the pre-image and Translate pre-image ABC 2 left and 6 down. label the new point. What are the coordinates of the image and pre-image? Example: Move the figure left 2 units and up 5 units. A What are the coordinates of the pre-image and image? A' B' C C' D' B A B C D Are the line segments in the pre-image and image the same Are the line segments in the pre-image and image the same length? In other words, was the size of the figure preserved? length? In other words, was the size of the figure preserved? Both the pre-image and image are congruent. Both the pre-image and image are congruent. click to reveal click to reveal Slide 15 / 230 Slide 16 / 230 Translate pre-image ABCD 4 right and 1 down. Translate pre-image ABCD 5 left and 3 up. What are the coordinates of the image and pre-image? What are the coordinates of the image and pre-image? A A B D B C C D Are the line segments in the pre-image and image the same Are the line segments in the pre-image and image the same length? In other words, was the size of the figure preserved? length? In other words, was the size of the figure preserved? Both the pre-image and image are congruent. Both the pre-image and image are congruent. Click click to reveal Slide 17 / 230 Slide 18 / 230 Translations Rule Translations Rule Translating left/right changes the x-coordinate. A rule can be written to describe translations on the coordinate plane. Look at the following rules and Translating up/down changes the y-coordinate. coordinates to see if you can find a pattern. 2 Left and 5 Up 2 Left and 6 Down 2 Left and 5 Up 2 Left and 6 Down A (3,-1) A' (1,4) A (-2,7) A' (-4,1) A (3,-1) A' (1,4) A (-2,7) A' (-4,1) B (8,-1) B' (6,4) B (-3,1) B' (-5,-5) B (8,-1) B' (6,4) B (-3,1) B' (-5,-5) C (7,-3) C' (5,2) C (-6,3) C' (-8,-3) C (7,-3) C' (5,2) C (-6,3) C' (-8,-3) D (2, -4) D' (0,1) D (2, -4) D' (0,1) 5 Left and 3 Up 4 Right and 1 Down 5 Left and 3 Up 4 Right and 1 Down A (3,2) A' (-2,5) A (-5,4) A' (-1,3) A (3,2) A' (-2,5) A (-5,4) A' (-1,3) B (7,1) B' (2,4) B (-1,2) B' (3,1) B (7,1) B' (2,4) B (-1,2) B' (3,1) C (4,0) C' (-1,3) C (-4,-2) C' (0,-3) C (4,0) C' (-1,3) C (-4,-2) C' (0,-3) D (2,-2) D' (-3,1) D (-6, 1) D' (-2,0) D (2,-2) D' (-3,1) D (-6, 1) D' (-2,0)

Slide 19 / 230 Slide 20 / 230 Translations Rule Translations Rule A rule can be written to describe translations on the coordinate Translating left/right changes the x-coordinate. plane. · Left subtracts from the x-coordinate · Right adds to the x-coordinate 2 units Left … x-coordinate - 2 y-coordinate stays click rule = (x - 2, y) Translating up/down changes the y-coordinate. · Down subtracts from the y-coordinate 5 units Right & 3 units Down… x-coordinate + 5 · Up adds to the y-coordinate y-coordinate - 3 click rule = (x + 5, y - 3) Slide 21 / 230 Slide 22 / 230 Translations Rule 1 What rule describes the translation shown? E' Write a rule for each translation. A (x,y) (x - 4, y - 6) D' 2 Left and 5 Up 2 Left and 6 Down F' B (x,y) (x - 6, y - 4) E A (3, -1) A' (1, 4) A (-2, 7) A' (-4, 1) D B (8, -1) B' (6, 4) B (-3, 1) B' (-5, -5) C (x,y) (x + 6, y + 4) F G' C (7, -3) C' (5, 2) C (-6, 3) C' (-8, -3) D (x,y) (x + 4, y + 6) D (2, -4) D' (0, 1) click to reveal (x, y) (x-2, y-6) G (x, y) (x-2, y+5) click to reveal click to reveal click to reveal 5 Left and 3 Up 4 Right and 1 Down A (3, 2) A' (-2, 5) A (-5, 4) A' (-1, 3) B (7, 1) B' (2, 4) B (-1, 2) B' (3, 1) C (4, 0) C' (-1, 3) C (-4, -2) C' (0, -3) D (2, -2) D' (-3, 1) D (-6, 1) D' (-2, 0) (x, y) (x+4, y-1) click to reveal (x, y) (x-5, y+3) click to reveal click to reveal click to reveal Slide 23 / 230 Slide 24 / 230 2 What rule describes the translation shown? 3 What rule describes the translation shown? A (x,y) (x, y - 9) A (x,y) (x + 8, y - 5) E E' B (x,y) (x, y - 3) B (x,y) (x - 5, y - 1) D D' C C (x,y) (x + 5, y - 8) (x,y) (x - 9, y) F F' D (x,y) (x - 8, y + 5) D E (x,y) (x - 3, y) D G G' F E' D' F' G G'

Slide 25 / 230 Slide 26 / 230 4 What rule describes the translation shown? 5 What rule describes the translation shown? A (x,y) (x - 3, y + 2) E' A (x,y) (x - 3, y + 2) E B (x,y) (x + 3, y - 2) D' F' D B (x,y) (x + 3, y - 2) F E' E D' C (x,y) (x + 2, y - 3) D F F' C (x,y) (x + 2, y - 3) G' D (x,y) (x - 2, y + 3) G D (x,y) (x - 2, y + 3) G G' Slide 27 / 230 Slide 28 / 230 Rotations Rotations Return to Table of Contents Slide 29 / 230 Slide 30 / 230 Rotations A rotation (turn) moves a figure around a point. This point can be the index finger or it can be some other point. This point is called the point of rotation . Rotations The person's finger is the point of rotation for each figure. P

Slide 31 / 230 Slide 32 / 230 When you rotate a figure, you can describe the rotation by How is this figure giving the direction (clockwise or counterclockwise) and rotated about the A B the angle that the figure is rotated around the point of In order to origin? rotation. Rotations are counterclockwise unless you are determine the angle, draw told otherwise. Describe each of the rotations. two rays (one In a coordinate from the point D C of rotation to plane, each pre-image B' quadrant represents C' point, the other from the 90º. point of rotation to the A' image point). D' Measure this angle. This figure is rotated This figure is rotated 90º click to reveal 180º clockwise counterclockwise about about point B. point A. Check to see if the pre-image and image are congruent. Slide 33 / 230 Slide 34 / 230 Rotations Rotations The sum of the two rotations (clockwise and counterclockwise) is 360 degrees. The following descriptions describe the same rotation. If you have one rotation, you can calculate the other by subtracting What do you notice? from 360. Can you give your own example? Slide 35 / 230 Slide 36 / 230 7 How is this figure rotated about point the origin? 6 How is this figure rotated about point A? (Choose (Choose more than one answer.) more than one answer.) A clockwise A clockwise B counterclockwise B counterclockwise C 90 degrees C 90 degrees D 180 degrees D 180 degrees E 270 degrees E 270 degrees Check to see if the pre-image and image are congruent. Check to see if the pre-image and image are congruent.

Slide 37 / 230 Slide 38 / 230 Rotations Teachers: Now let's look at the same figure and see A B Use this Mathematical Practice Pull Tab for what happens to the the next 3 example slides & the "General coordinates when we rotate a figure 90º Formula" slide that follows. D C counterclockwise. B' C' Write the coordinates for the pre-image and A' image. D' What do you notice? Slide 39 / 230 Slide 40 / 230 Rotations Rotations What happens to B What happens to the coordinates in the coordinates in a half-turn? a 90º clockwise? B A A C Write the Write the coordinates for the coordinates for the pre-image and D C pre-image and D image. C' D' image. A' D' What do you B' What do you notice? notice? B' A' C' Slide 41 / 230 Slide 42 / 230 Rotations 8 What are the new coordinates of a point A (5, -6) after 90º rotation clockwise? Summarize what happens to the coordinates during a rotation? A (-6, -5) 90º Counterclockwise: B (6, -5) Half-turn: C (-5, 6) D (5, -6) 90º Clockwise: