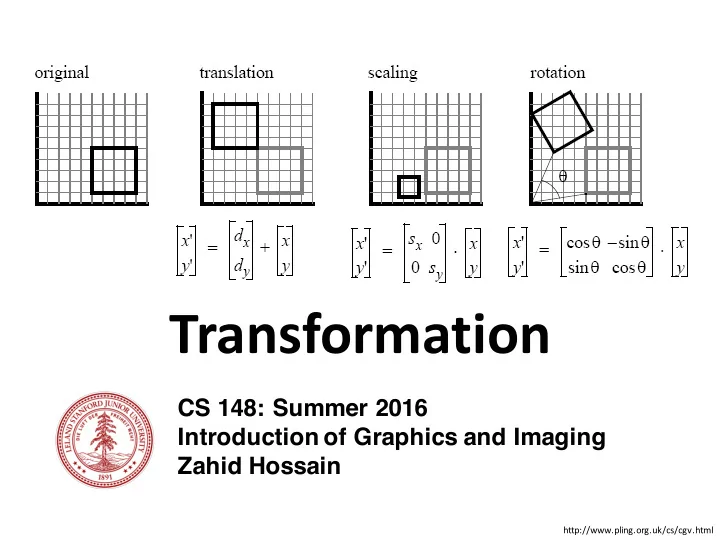
transformation
play

Transformation CS 148: Summer 2016 Introduction of Graphics and - PowerPoint PPT Presentation

Mar 26, 2023 •727 likes •1.49k views

Transformation CS 148: Summer 2016 Introduction of Graphics and Imaging Zahid Hossain http://www.pling.org.uk/cs/cgv.html Placement of Objects Fisher et al. (2012) 2 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016)

  1. Transformation CS 148: Summer 2016 Introduction of Graphics and Imaging Zahid Hossain http://www.pling.org.uk/cs/cgv.html

  2. Placement of Objects Fisher et al. (2012) 2 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  3. Placement of Objects Oriented Fisher et al. (2012) 3 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  4. Placements of Objects Translated Fisher et al. (2012) 4 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  5. Points and Vectors y p x Origin z 5 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  6. Points and Vectors y x Vector Points Origin z 6 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  7. Transformations What? Just functions acting on points: • Why? • • Viewing: • Convert between coordinates systems • Virtual camera, e.g. perspective projections • Modeling: • Create objects in a convenient orientation • Use multiple instances of a given shape • Kinematics – characters/robots 7

  8. Linear Transformation 8 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  9. Linear Transformation 9 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  10. Linear Transformation 10 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  11. Linear Transformation Lines Map to Lines 11 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  12. Common Transformation Rotate Scale Shear 12

  13. 13

  14. Composing Transformations First Rotate 45° 14 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  15. Composing Transformations Then Scale 2x along y 15 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  16. Composing Transformations Scale Rotation Order of transformations 16 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  17. Composing Transformation Not Commutative Rotate -> Scale Scale -> Rotate 17 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  18. Translation 18 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  19. Homogenous Coordinates For any non-zero c 19 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  20. Homogenous Coordinates 20 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  21. Homogenous Coordinates 21 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  22. Homogenous Coordinates 4D Homogenous Coordinate 3D Cartesian Coordinate 22 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  23. Homogenous Coordinates (x,y,w) w-axis w=1 (x/w,y/w,1) x,y-axis 23 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  24. Homogenous Coordinates z-axis Decrease w z=1 x,y-axis 24 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  25. Homogenous Coordinates z-axis Decrease w z=1 x,y-axis 25 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  26. Homogenous Coordinates 26 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  27. Homogenous Coordinates Represents a Vector! (Homogenous Coordinates express both Vectors and Points) 27 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  28. Back to Translation Homogenous Coordinate Homogenous Coordinate 28 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  29. Some Exercise Convert 3D Cartesian Coordinate to Homogenous Coordinate (3,4,2) : 29 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  30. Some Exercise Convert 3D Cartesian Coordinate to Homogenous Coordinate (3,4,2) : (3,4,2,1) 30 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  31. Some Exercise Convert 3D Cartesian Coordinate to Homogenous Coordinate (3,4,2) : (3,4,2,1) Convert Homogenous Coordinate to Cartesian Coordinate (3,4,2,2) : 31 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  32. Some Exercise Convert 3D Cartesian Coordinate to Homogenous Coordinate (3,4,2) : (3,4,2,1) Convert Homogenous Coordinate to Cartesian Coordinate (3,4,2,2) : (1.5,2,1) 32 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  33. Some Exercise Rotate about the center of the box 33 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  34. Some Exercise Translate to center 34 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  35. Some Exercise Rotate 35 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  36. Some Exercise Translate back 36 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  37. Coordinate System 37 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  38. Coordinate System 38 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  39. Coordinate System 39 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  40. Coordinate System: Rotation 40 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  41. Coordinate System: Rotation 41 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  42. Coordinate System: Rotation 42 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  43. Coordinate System: Hierarchy 43 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  44. Coordinate System: Hierarchy 44 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  45. Coordinate System: Hierarchy 45 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  46. Interpreting Transformations 46 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  47. Two Interpretations • With respect to Global Frame • With respect to Local Frame 47 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  48. Coordinate System: Hierarchy 48 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  49. w.r.t Global Frame Rotate(45°) Translate(0,1) Translate(1,1) Combined = Translate(0,1) Rotate(45°) Translate(1,1) Order of Transforms 49 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  50. w.r.t Local Frame Rotate(45°) Translate(1,1) Translate(0,1) Combined = Translate(0,1) Rotate(45°) Translate(1,1) Order of Transform 50 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  51. w.r.t Local Frame Rotate(45°) Translate(1,1) Translate(0,1) Combined = Translate(0,1) Rotate(45°) Translate(1,1) Order of Transform Both interpretations are equivalent 51 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  52. Hierarchical Modeling translate(0,4) drawTorso() pushMatrix() translate(1.5,0) rotateX(leftHipRotate) drawThigh() pushMatrix() translate(0,-2) rotateX(leftKneeRotate) drawLeg() ... popMatrix() popMatrix() pushMatrix() y translate(-1.5,0) rotateX(rightHipRotate) // Draw the right side x Matrix Stack ... ... CurrentMatrix = Translate(0,4) 52 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  53. Hierarchical Modeling translate(0,4) drawTorso() pushMatrix() translate(1.5,0) rotateX(leftHipRotate) drawThigh() pushMatrix() translate(0,-2) rotateX(leftKneeRotate) drawLeg() ... popMatrix() popMatrix() pushMatrix() y translate(-1.5,0) rotateX(rightHipRotate) Translate(0,4) // Draw the right side x Matrix Stack ... ... CurrentMatrix = Translate(0,4) 53 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

  54. Hierarchical Modeling translate(0,4) drawTorso() pushMatrix() translate(1.5,0) rotateX(leftHipRotate) drawThigh() pushMatrix() translate(0,-2) rotateX(leftKneeRotate) drawLeg() ... popMatrix() popMatrix() pushMatrix() y translate(0,4) translate(1.5,0) rotateX(leftHipRotate) translate(-1.5,0) rotateX(rightHipRotate) translate(0,4) // Draw the right side x Matrix Stack ... ... CurrentMatrix = translate(0,4) translate(1.5,0) rotateX(leftHipRotate) translate(0,-2) rotate(leftKneeRotate) 54 CS 148: Introduction to Computer Graphics and Imaging (Summer 2016) – Zahid Hossain

Download Presentation
Download Policy: The content available on the website is offered to you 'AS IS' for your personal information and use only. It cannot be commercialized, licensed, or distributed on other websites without prior consent from the author. To download a presentation, simply click this link. If you encounter any difficulties during the download process, it's possible that the publisher has removed the file from their server.

Recommend

CHAPTER 11: MODEL TRANSFORMATION Transformation Definition Transformation Tool 2 Agenda

CHAPTER 11: MODEL TRANSFORMATION Transformation Definition Transformation Tool 2 Agenda

Architecture and Modelling of Information Systems (D0I71A) Prof. dr. Monique Snoeck CHAPTER 11: MODEL TRANSFORMATION Transformation Definition Transformation Tool 2 Agenda Model Transformations General approach Transformation

985 views • 59 slides
Composing Transformation Composing Transformation Composing Transformation the process of

Composing Transformation Composing Transformation Composing Transformation the process of

Composing Transformation Composing Transformation Composing Transformation the process of applying Matrix multiplication is associative several transformation in succession to form one M3 x M2 x M1 = (M3 x M2) x M1 = M3 x (M2 x

485 views • 9 slides
Ecological transformation When ecological knowledge and transformation in the social

Ecological transformation When ecological knowledge and transformation in the social

Ecological transformation When ecological knowledge and transformation in the social practices as the goal of environmental studies ------- Ecological transformation is best understood as an ongoing process of wide-ranging

637 views • 48 slides
Transformation Management Office Rick Baniak November 16, 2018 Chief Transformation Officer

Transformation Management Office Rick Baniak November 16, 2018 Chief Transformation Officer

Transformation Management Office Rick Baniak November 16, 2018 Chief Transformation Officer (CTO) Responsibilities Develop culture of transformation throughout University Implement the Transformation Project Portfolio as identified by

461 views • 28 slides
Transformation Center: Supporting health system transformation Chris DeMars, Director of Systems

Transformation Center: Supporting health system transformation Chris DeMars, Director of Systems

Transformation Center: Supporting health system transformation Chris DeMars, Director of Systems Innovation Summer Boslaugh, Transformation Analyst POLICY AND ANALYTICS Transformation Center Purpose of todays presentation Overview of

594 views • 14 slides
Transformation launch event HSCP Transformation Programme Launch 09:15 09:25 Judith Proctor

Transformation launch event HSCP Transformation Programme Launch 09:15 09:25 Judith Proctor

Transformation launch event HSCP Transformation Programme Launch 09:15 09:25 Judith Proctor Background and Transformation Journey 09:25 09:40 Tony Duncan Our Strategic Direction 09:40 09:45 Jess Brown Transformation Programme

461 views • 25 slides
1 View ing Transform ation Eye Coordinate Fram e Recall OpenGL way to set cam era:

1 View ing Transform ation Eye Coordinate Fram e Recall OpenGL way to set cam era:

3 D view ing under the hood CS 4 7 3 1 : Com put e r Gr a phics Le ct ur e 1 2 : M or e 3 D Vie w ing Modeling Viewing Projection Em m anuel Agu Transformation Transformation Transformation Viewport

216 views • 4 slides
School Transformation Fund Webinar Slides May 4, 2018 What is the Transformation Fund? The

School Transformation Fund Webinar Slides May 4, 2018 What is the Transformation Fund? The

School Transformation Fund Webinar Slides May 4, 2018 What is the Transformation Fund? The School Transformation Fund aims to increase the number of students in great schools by providing customized support to districts committed to transforming

439 views • 21 slides
Strategy for City Transformation (Part 4) Sunday November 25, Strategy for City Transformation

Strategy for City Transformation (Part 4) Sunday November 25, Strategy for City Transformation

Strategy for City Transformation (Part 4) Sunday November 25, Strategy for City Transformation (Review) What do we mean by City Transformation? By City Transformation we are primarily talking about spiritual transformation resulting

380 views • 34 slides
DIGITAL TRANSFORMATION CENTER The Digital Transformation Center, supports companies to close

DIGITAL TRANSFORMATION CENTER The Digital Transformation Center, supports companies to close

DIGITAL TRANSFORMATION CENTER The Digital Transformation Center, supports companies to close their digital skill gaps through training programs in order to promote an effective digital transformation. Team Mauricio Ros Daniel Fernndez

417 views • 22 slides
Kokomo Transformation Zone 1 Kokomo School Corporation Transformation Zone 2 KSC

Kokomo Transformation Zone 1 Kokomo School Corporation Transformation Zone 2 KSC

Kokomo Transformation Zone 1 Kokomo School Corporation Transformation Zone 2 KSC Superintendent : Dr. Jeff Hauswald KSC Assistant Superintendent : Dr. Mike Sargent KSC Transformation Zone Director : Erin Stalbaum Pettit Park

265 views • 22 slides
! Institut for Informatics Digital transformation is ... ... the change of the analog to digital,

! Institut for Informatics Digital transformation is ... ... the change of the analog to digital,

Digital Transformation A Game Changer How Does the Digital Transformation Affect Informatics as a Scientific Discipline? Manfred Broy Technische Universitt Mnchen ! Institut for Informatics Digital transformation is ... ... the

887 views • 49 slides
The New Rules of Bank Transformation Branch transformation strategy expert Branch

The New Rules of Bank Transformation Branch transformation strategy expert Branch

Branch Transformation February 1, 2017 The New Rules of Bank Transformation Branch transformation strategy expert Branch Transformation February 1, 2017 David Faulkner Before founding Next Branch Strategies in 2015, worked at top

503 views • 16 slides
Your Digital Transformation Partner Your Digital Transformation Partner INTRODUCTION Experienced

Your Digital Transformation Partner Your Digital Transformation Partner INTRODUCTION Experienced

Your Digital Transformation Partner Your Digital Transformation Partner INTRODUCTION Experienced IT/Web Services Team Focused on B2B digital transformation solutions CUSTOMER FACING SYSTEMS 24 year track record 200+ IT systems and

296 views • 18 slides
Modified Box-Cox Transformation and Manly Transformation with Failure Time Data Lakhana

Modified Box-Cox Transformation and Manly Transformation with Failure Time Data Lakhana

Modified Box-Cox Transformation and Manly Transformation with Failure Time Data Lakhana Watthanacheewakul Backgrounds Many procedures require data to be approximately normal. A transformation that transforms the data set to A

759 views • 50 slides
Outline 1. Introduction: Economic Transformation: always the objective 2. Gold Mining 1998-2010:

Outline 1. Introduction: Economic Transformation: always the objective 2. Gold Mining 1998-2010:

Tanzania & Extractives ------ Transformation or just BIG Numbers? Alan R. Roe UNU-WIDER and University of Warwick Presentation to REPOA/WIDER Conference Transformation for Growth, Employment and Poverty Reduction Dar es Salaam - November

1.04k views • 41 slides
Transformations & Transformations & Coordinate Systems Coordinate Systems CSCD 472?

Transformations & Transformations & Coordinate Systems Coordinate Systems CSCD 472?

Transformations & Transformations & Coordinate Systems Coordinate Systems CSCD 472? Slide 1 4/5/10 Transformations: Basic Definitions Transformations: Basic Definitions Basic definitions Coordinate systems in RenderMan are always

498 views • 14 slides
Computer graphics 2: Graduate seminar in computational aesthetics Angus Forbes

Computer graphics 2: Graduate seminar in computational aesthetics Angus Forbes

Computer graphics 2: Graduate seminar in computational aesthetics Angus Forbes evl.uic.edu/creativecoding/cs526 Homework 2 RJ ongoing... - Follow the suggestions in the Research Journal handout and find and describe three papers OR

480 views • 23 slides
Nquire ask anything Anis Abboud, Chris Snyder, Mario Finelli Device 1 Device 2 Device 1

Nquire ask anything Anis Abboud, Chris Snyder, Mario Finelli Device 1 Device 2 Device 1

Nquire ask anything Anis Abboud, Chris Snyder, Mario Finelli Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2 Device 1 Device 2

821 views • 49 slides
HCI in the software Iterative design and prototyping process Design rationale the

HCI in the software Iterative design and prototyping process Design rationale the

HCI in the software process Software engineering and the design process chapter 6 for interactive system s Usability engineering HCI in the software Iterative design and prototyping process Design rationale the software

505 views • 4 slides
COMPUTER GRAPHICS COURSE Viewing and Projections Georgios Papaioannou - 2014 VIEWING

COMPUTER GRAPHICS COURSE Viewing and Projections Georgios Papaioannou - 2014 VIEWING

COMPUTER GRAPHICS COURSE Viewing and Projections Georgios Papaioannou - 2014 VIEWING TRANSFORMATION The Virtual Camera All graphics pipelines perceive the virtual world Y through a virtual observer (camera), also positioned in the 3D

661 views • 47 slides
Camera Calibration of C-Arm devices Quirin Meyer March 17, 2006 1 Introduction and Motivation

Camera Calibration of C-Arm devices Quirin Meyer March 17, 2006 1 Introduction and Motivation

Camera Calibration of C-Arm devices Quirin Meyer March 17, 2006 1 Introduction and Motivation C-Arm CT systems are, as ordinary CT scanners, applied in medical imaging and are capable of generating tomographic images based on an X-ray source.

737 views • 7 slides
1 Projections Orthographic Projection To lower dimensional space (here 3D -> 2D)

1 Projections Orthographic Projection To lower dimensional space (here 3D -> 2D)

To Do Computer Graphics Questions/concerns about assignment 1? Remember it is due Jan 30. Ask me or TAs re problems CSE 167 [Win 17], Lecture 5: Viewing Ravi Ramamoorthi http://viscomp.ucsd.edu/classes/cse167/wi17 Motivation Demo

291 views • 6 slides
Virtual Telescope and Stars Guide service for mobile devices (Progress report) (Progress report)

Virtual Telescope and Stars Guide service for mobile devices (Progress report) (Progress report)

Virtual Telescope and Stars Guide service for mobile devices (Progress report) (Progress report) Alexandra Reyss, Petrozavodsk State University Sergey Balandin, Nokia Research Center 1/14 Outline 1. Motivation 2. Use-case scenarios 3.

585 views • 13 slides

More recommend