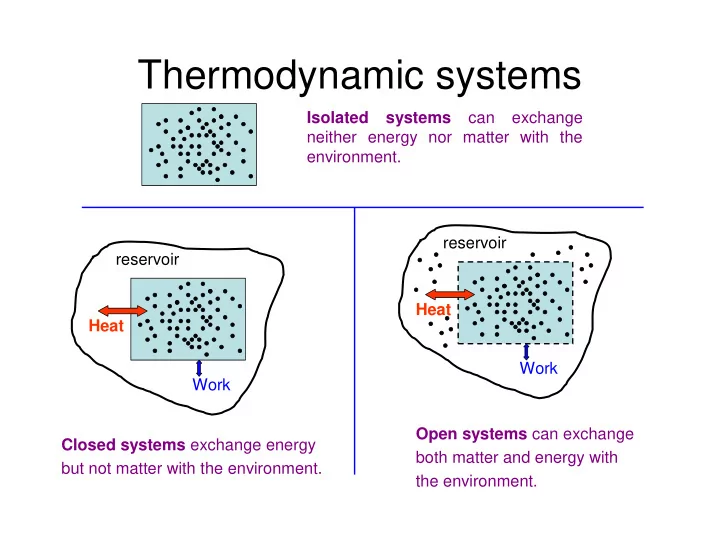

Thermodynamic systems Isolated systems can exchange neither energy nor matter with the environment. reservoir reservoir Heat Heat Work Work Open systems can exchange Closed systems exchange energy both matter and energy with but not matter with the environment. the environment.
Quasi-static processes Quasi-static processes : near equilibrium Initial state, final state, intermediate state: p, V & T well defined Sufficiently slow processes = any intermediate state can considered as at thermal equilibrium. Thermal equilibrium means that It makes sense to define a temperature. Examples of quasi-static processes: - isothermal: T = constant - isochoric: V = constant - isobaric: P = constant - adiabatic: Q = 0
Work in thermodynamics Expansion: work on piston positive, work on gas negative Compression: work on piston negative, work on gas positive
Work during a volume change = dW F dx . = p Adx . = pdV V 2 = W pdV ∫ ⇒ V 1
Work in pV diagrams Work done equals area under curve in pV diagram Careful with the signs…
1 st Law of Thermodynamics Heat is negative Work is negative when it leaves when it is done on the system the system Heat is positive Work is positive when it enters when it is done by the system the system ∆ = − U Q W Conservation of energy
1 st Law of Thermodynamics Heat is negative Work is negative when it leaves when it is done on the system the system Heat is positive Work is positive when it enters when it is done by the system the system = − dU dQ pdV Conservation of energy
State Functions (c) (a) (b) a. isobaric a. isochoric isothermal b. isochoric b. isobaric V = f W V pdV = − = − W p V V W p V V ( ) ( ) ∫ 1 2 1 2 2 1 i • The work done by a system depends on the initial and final states and on the path � it is not a state function. • Amount of heat transferred also depends on the initial, final, and intermediate states � it is not a state function either.
State Functions ∆ = − = − U Q W U U 2 1 The internal energy U is a state function: the energy gain (loss) only depends on the initial and final states, and not on the path. Even though Q and W depend on the path, ∆ U does not!
CPS question This pV –diagram shows two ways to take a system from state a (at lower left) to state c (at upper right): • via state b (at upper left), or • via state d (at lower right) For which path is W > 0? A. path abc only B. path adc only C. both path abc and path adc D. neither path abc nor path adc E. The answer depends on what the system is made of.
CPS question A system can be taken from state a to state b along any of the three paths shown in the pV – diagram. If state b has greater internal energy than state a , along which path is the absolute value | Q | of the heat transfer the greatest? A. path 1 B. path 2 C. path 3 D. | Q | is the same for all three paths. E. not enough information given to decide
Thermodynamic Processes: • Adiabatic: no heat transfer (by insulation or by very fast process) Q=0 → → → → U 2 – U 1 = -W • Isochoric: constant volume process (no work done) W=0 → → U 2 – U 1 = Q → → • Isobaric: constant pressure process p=const. → → W = p (V 2 – V 1 ) → → • Isothermal: constant temperature process (heat may flow but very slowly so that thermal equilibrium is not disturbed) ∆ ∆ ∆ ∆ U=0, Q =-W only for ideal gas. Generally ∆ ∆ ∆ ∆ U, Q, W not zero any energy entering as heat must leave as work
Thermodynamic processes
First Law for Several Types of Processes Isolated systems: Adiabatic processes Cyclic processes P i, f = = Q W 0 V initial state = final state = 0 → ∆ = Q U 0 ∆ = U 0 → ∆ = − → = U W U U i f → = Q W Expansion: U decreases The internal energy Compression: U increases Energy exchange between of an isolated systems “heat” and “work” remains constant
More about cyclic processes P i, f V Work equals the area enclosed by the curves (careful with the sign!!!)
CPS question An ideal gas is taken around the cycle shown in this pV –diagram, from a to b to c and back to a . Process b → c is isothermal. For this complete cycle, A. Q > 0, W > 0, and ∆ U = 0. B. Q > 0, W > 0, and ∆ U > 0. C. Q = 0, W > 0, and ∆ U < 0. D. Q = 0, W < 0, and ∆ U > 0. E. Q > 0, W = 0, and ∆ U > 0.
Important formulas ∆ U = Q-W (1 st law) V 2 = W pdV (work during a volume change) ∫ V 1 pV=nRT (Ideal gas law) C V =f /2 nR (Equipartition theorem)
Ideal gas: isochoric process Isochoric process: V = constant P = p V nRT 2 2 2 V → = = W V pdV 2 0 ∫ 1 1 = − Q C T T ( ) = p V nRT V 2 1 (C V: heat capacity 1 1 = ∆ C T at constant volume) V V 1,2 V ∆ = − U Q W → ∆ = = V ∆ U Q C T reservoir During an isochoric process, heat enters Heat (leaves) the system and increases (decreases) the internal energy.
Ideal gas: isobaric process P pV = nRT Isobaric process: p = constant 2 2 V 2 → = = − = ∆ W pdV p V V p V 2 1 ( ) ∫ 2 1 V 1 = pV Nk T = − Q C T T ( ) B 1 1 p 2 1 (C P: heat capacity V 1 V 2 = ∆ C T V at constant pressure) p → ∆ = − U Q W reservoir = ∆ − ∆ C T p V P Heat During an isobaric expansion process, heat enters the system. Part of the heat is used by the system to do work on the Work environment; the rest of the heat is used to increase the internal energy.
Ideal gas: isothermal process pV = nRT 1 P Isothermal process: T = constant ∆ = ∆ = T U 0 0 2 ⇒ nRT V V = = W 2 pdV 2 dV ∫ ∫ V V V V 1 V 2 V 1 1 dV V = nRT 2 ∫ V Expansion: V 1 heat enters the system V all of the heat is used by the system = nRT 2 ln to do work on the environment. V 1 V Compression: → = = Q W nRT ln V 2 the work done on the system increases its internal energy, 1 all of the energy leaves the system at the same time as the heat is removed.
Heat capacities of an Ideal gas Consider an isobaric process p=constant = ∆ Q C T p p From the 1 st Law of Thermodynamics: = = + dQ C dT dU pdV p p = + C dT C dT pdV but p V = ⇒ dU C dT V From the Ideal gas law: = + = = pV nRT pdV Vdp pdV nRdT ⇒ = + = + C dT C dT nRdT C C nR p V p V ⇒ ⇒
Heat capacities of an Ideal gas = + C C nR p V + f 2 = C p nR f ⇒ f = #degrees = C nR 2 of freedom V 2 C + + f f f 2 2 p = = nR nR / ⇒ C f 2 2 V For a monoatomic gas f=3 C 5 p = = = C nR ; 5 / 3 1 . 67 p ⇒ C 2 V
Molar heat capacities of various gases at (25 C) Gas Cp Cv Cv/R Cp-Cv (Cp-Cv)/R Monoatomic He 20.79 12.52 1.51 8.27 0.99 Ne 20.79 12.68 1.52 8.11 0.98 Ar 20.79 12.45 1.50 8.34 1.00 Kr 20.79 12.45 1.50 8.34 1.00 Xe 20.79 12.52 1.51 8.27 0.99 Diatomic N2 29.12 20.80 2.50 8.32 1.00 H2 28.82 20.44 2.46 8.38 1.01 O2 29.37 20.98 2.52 8.39 1.01 CO 29.04 20.74 2.49 8.40 1.00 Polyatomic CO2 36.62 28.17 3.39 8.45 1.02 N2O 36.90 28.39 3.41 8.51 1.02 H2S 36.12 27.36 3.29 8.76 1.05
Ideal gas: adiabatic process Adiabatic process: Q = 0 P p = p V T ( , ) 2 V V = = W 2 pdV 2 p V T dV ( , ) ∫ ∫ V V 1 1 1 = pV Nk T V 2 V 1 V B → = d pV d nRT ( ) ( ) → + = pdV Vdp nRdT 2 + = − pdV Vdp pdV = − = − dU dW pdV f → = − C dT pdV V f → = − n RdT pdV 2 f is the # of degrees of freedom
Ideal gas: adiabatic process (contd) 2 + = − pdV Vdp pdV P f p = p V T ( , ) 2 2 → + + = Vdp pdV ( 1 ) 0 f 1 2 , and dividing by pV γ = + ( 1 ) let f V 2 V 1 V dp dV + γ = 0 p V dp dV p V + ∫ γ = 0 ∫ p V p V 1 1 p V → + γ = ln ln 0 p V 1 1 γ pV γ γ → = → = = pV p V ln 0 constant γ 1 1 p V 1 1
Ideal gas: adiabatic process (contd) = − ∆ = − ∆ W U nC T P V γ = pV constant 2 = − nC T T ( ) V 1 2 C = − p V p V V ( ) 1 R 1 1 2 2 V 2 V 1 1 V = − p V p V ( ) γ − 1 1 2 2 1 Using: γ γ = = pV p V constant 1 1 1 1 1 γ → = − W p V γ − γ − γ − 1 1 V 1 V 1 ( 1 ) 1 2
Ideal gas: adiabatic process (contd) γ γ = = pV p V P constant γ = pV 1 1 constant 2 1 = p V nRT p V T → = 1 1 1 1 1 1 = p V nRT p V T V 2 V 1 2 2 2 2 2 2 V γ p = V γ γ = → p V p V 1 2 γ p 1 1 2 2 V 2 1 γ − V T 1 → = 2 1 γ − V T 1 1 2 γ − γ − = = T V 1 T V 1 constant or 1 1 2 2
Recommend
More recommend